Jump Game(Java,C++)

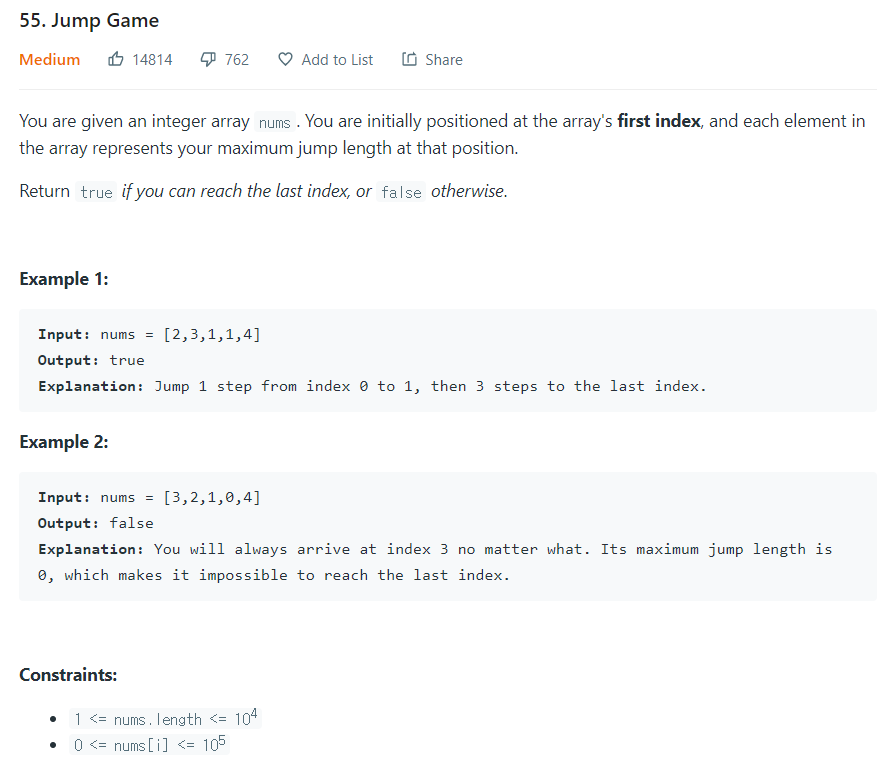
Jump Game문제도 오래전에 풀어봤지만 DP 테이블 방식으로는 처음 풀어보는 문제다. 문제를 풀면 풀 수록 DP와 관련된 새로운 지식을 얻게되는거 같아서 매우 신기한거같다. 지금까지 풀었던 House Robber 같은 문제들은 선택 혹은 선택하지 않는다, 그리고 구간에 겹치는 중복 부분을 어떻게 하면 DP로 최적화 할 수 있을까의 문제였다. House Robber 같은 경우 Max 값으로 i-1 값 혹은 i-2 + 현재값으로 구했고, House Robber 2같은 경우 필요한 부분을 잘라서 DP를 써줬다. 그런데 이 문제는 조금은 색다로운 접근이 필요했다.

우리는 무조건 첫번째 index에서 시작한다. 그리고 그 index에 있는 숫자만큼 앞으로 나갈 수 있다. 마지막 index까지 도착하면은 true 혹은 false를 리턴하는 문제다. 만약 2중 for 룹으로 모든 구간을 하나씩 탐색했다면은 당연히 TLE다. 그렇지만 DP를 적용하면 그 중복되는 구간을 줄일 수 있는데 그 방법을 생각하는게 참 어려웠다.

일단 2중 for 룹을 사용하는거는 똑같다. 다만 생각하고 있어야할 조건은 존재한다.

1. 첫번째 index는 무조건 True 값이다
2. [2,3,1] 과 같이 만약 현재 값 전에 있는 숫자를 더했을때 내 현재 위치 index 보다 크면은 우리는 점프를 true로 바꾼다
3. [2,0,1] 과 같이 현재 값 바로 전에 있는 숫자가 0이라 하더라도 그 전 구간을 볼때 조건에 따라서 점프가 true가 될 수 있다.

그렇기 떄문에 2중 for 룹의 두번째는 전부 탐색하되 한번이라도 true 구간이 있다면 점프를 true로 하고 break 해준다. 다만,
[0,0,4] 같이 절대로 앞으로 나갈 수 없는 경우는 배제해야한다 즉, 바로 전 숫자는 true 여야하는 조건이다.

Memoization 방식이 오히려 더 쉬워보였지만 DP 방식을 이해하니깐 더 재밌었다!

class Solution {
    public boolean canJump(int[] nums) {
        boolean[] dp = new boolean[nums.length]; 
        dp[0] = true; 
        for(int i = 1; i < nums.length; i++){
            for(int j = i -1; j >= 0; j--){
                if(dp[j] == true && j + nums[j] >= i){
                    dp[i] = true; 
                    break; 
                }
            }
        }
        
        return dp[nums.length - 1]; 
    }
}

class Solution {
public:
    bool canJump(vector<int>& nums) {
        vector<bool> dp(nums.size(),0); 
        dp[0] = true; 
        for(int i = 1; i < nums.size(); i++){
            for(int j = i - 1; j >= 0; j--){
                if(dp[j] == true && j + nums[j] >= i){
                    dp[i] = true; 
                    break; 
                }
            }
        }
        return dp[nums.size()-1]; 
    }
};