Longest Palindromic Subsequence

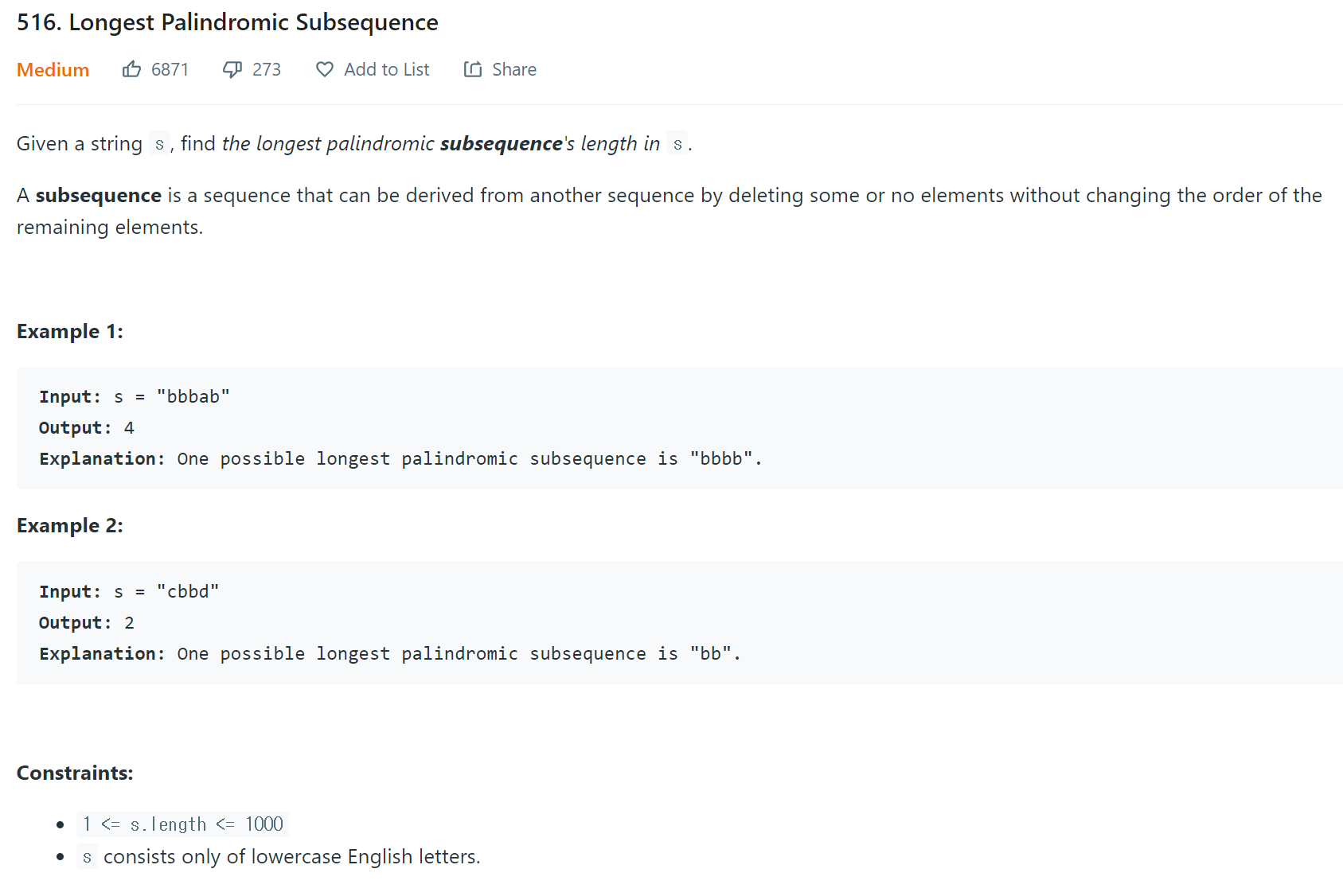
또 다른 유명한 DP문제를 풀어봤다. 바로 전 포스트에서 Palindrome 을 DP방식으로 찾는거는 또 한번의 룹으로 Palindrome을 줄이는것으로 시작되었다. 그리고 그 방법은 바로 i+1 j-1 범위에서 Palindrome이 완성됬다면 사이에 있는 구간은 모두 Palindrome임으로 Count를 업데이트 해줬다.

그런데 이 문제는 조금 다르게 Subsequence 문제다. 그 말은, 특정 범위에서 연속으로 이루어지는 문자열이 아니고 하나 이상의 문자를 지웠을때도 Palindrome이 만들어진다면? Palindrome인 문제다. 솔직히 전 문제랑 비슷하면서도 더 어려워서 많이 당황했었다.

그런데 차근차근 풀어보면은 뭔가 Best time to sell stock이랑 비슷하다 느꼈는데 양쪽의 캐릭터가 같지 않다면은 결국 한쪽 방향을 지웠을때의 최대값을 저장하면 됐었다.

내가 이 문제에서 굉장히 고민했던거는 앞에서 부터 dp 테이블을 채워줘도 괜찮지 않을까 했다가 시간을 너무 날렸다. 뭔가 더 공부해야겠지만 뒤에서부터 채워야지 문제가 풀어지는 DP 방식도 있는거같다. 열심히 해야겠다.

class Solution {
    public int longestPalindromeSubseq(String s) {
        int[][] dp = new int[s.length()][s.length()]; 
        // for(int i = 0;  i < s.length(); i++){
        //     dp[i][i] = 1; 
        //     for(int j = 0; j < i; j++){
        //         if(s.charAt(j) == s.charAt(i)){
        //             dp[j][i] = dp[j+1][i-1] + 2; 
        //         }
        //         else{
        //             dp[j][i] = Math.max(dp[j+1][i], dp[j][i-1]); 
        //         }
        //     }
        // }
        for(int i = s.length()-1; i >= 0; i--){
            dp[i][i] = 1; 
            for(int j = i+1; j < s.length(); j++){
                if(s.charAt(i) == s.charAt(j)){
                    dp[i][j] = dp[i+1][j-1] + 2; 
                }
                else{
                    dp[i][j] = Math.max(dp[i+1][j], dp[i][j-1]); 
                }
            }
        }

        return dp[0][s.length()-1]; 
    }
}