Longest Palindromic Substring

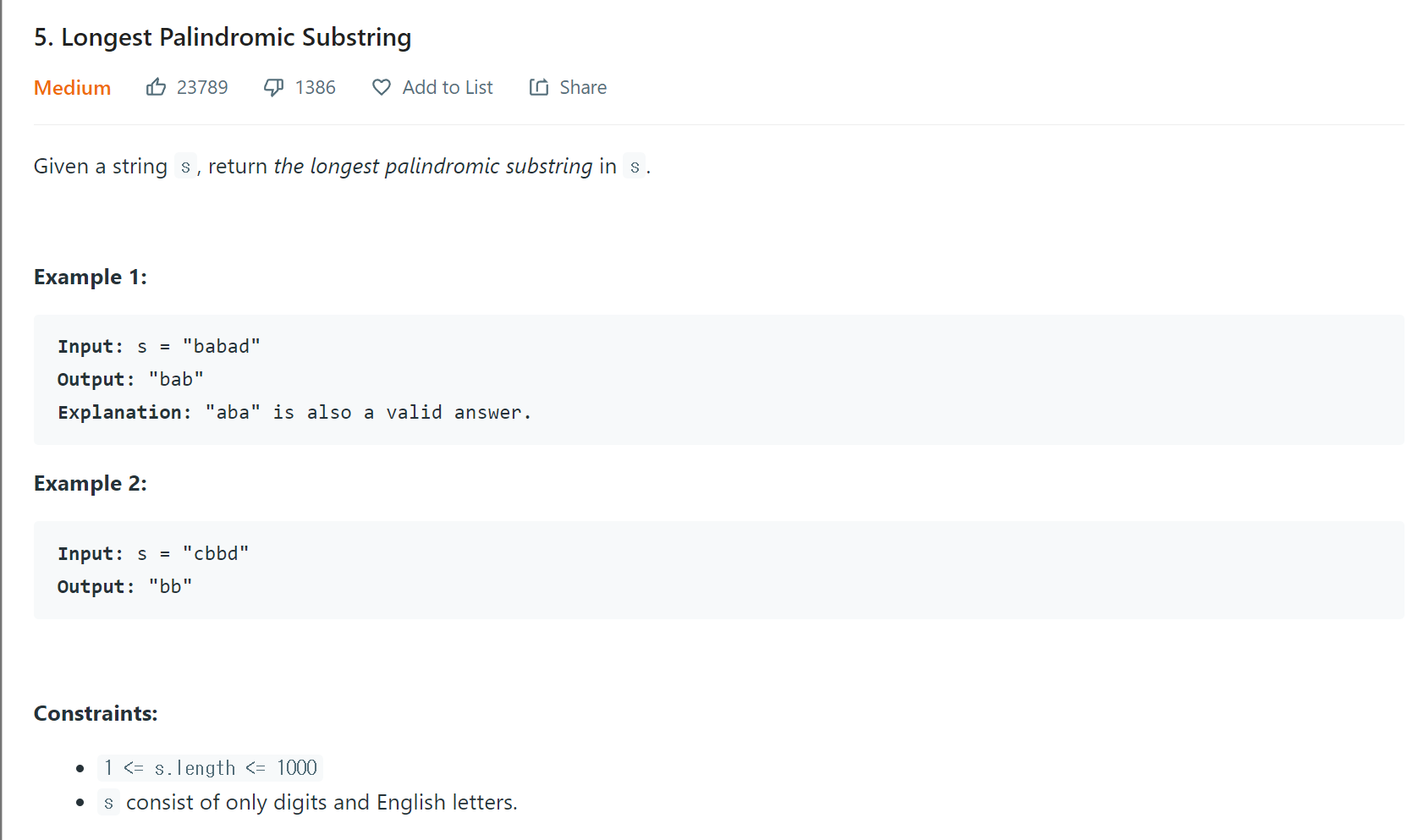
최근에 너무 쉬운 DP 문제들만 했던거 같아서 어려워 보이는 문제를 골라서 풀어봤다. 정말 엄청 유명한 문제여서 저번에도 풀었던 기억이 있지만 그때는 다르게 풀었고 꼭 DP를 활용해서 풀고 싶었는데 일단 첫 시도에서 뻘짓을 너무 많이 해서 결국 개털렸다. 꽤 많은 시간을 버리고 나서야 답을 확인했고 이 문제를 DP로 풀기 위해서 O(N) 의 방법을 버리고 O(N^2)의 방법을 선택해야 한다는것을 너무 늦게 알았다.

DP를 버리고 문제를 풀게 된다하면 결국 2중 루프를 사용하면서 필연적으로 Palindrome인지를 확인하는 함수를 한번 사용했을거다. 그리고 그 함수는 아마 루프 한번을 포함하기 때문에 결국 최악의 경우 Palindrome을 찾기 위해 3중 루프를 돌려야 한다는 뜻이다. DP 방식으로 이 문제에 접근하기 위해서는 쓸데 없는 Palindrome 함수를 줄이는것부터 시작했어야 했다.

만약 babab 가 있을 경우, 이미 aba가 palindrome인걸 안다면 babab를 확인하기 위해 aba를 또 체크해야할까? 아니다. 그렇기 때문에 2차원 DP 테이블을 사용해서 어느 위치부터 어느 위치까지 단어가 palindrome인것을 확인한다면 쓸데없는 Computation을 줄일 수 있다.

그렇기 때문에 필연적으로 2중 루프를 먼저 확인했고 만약에 Palindrome인것을 확인 한다면 j+1, i -1 범위에 단어 또한 전에 체크를 했는지 봐주고 계산을 해주면 된다. 2차원 DP테이블을 사용하는게 Matrix를 제외하고 사용해본적이 많이 없어서 어렵지만 그래도 꽤 재밌었던 문제였다.

class Solution {
    public String longestPalindrome(String s) {
        int start = 0, end = 0, max_ = 0; 
        boolean[][] dp = new boolean[s.length()][s.length()]; 
        for(int i = 0; i < s.length(); i++){
            for(int j  = 0; j <= i; j++){
                if(s.charAt(i) == s.charAt(j) && (i - j <= 2 || dp[j+1][i-1])){
                    dp[j][i] = true; 
                }
                if(dp[j][i] && max_ < i - j + 1){
                    start = j; 
                    end = i; 
                    max_ = i - j + 1; 
                }
            }
        }
        return s.substring(start, end + 1); 
    }
}