공부 내용

• Generative Model
• Generative Model 파라미터 수 감소 방법
• Auto-regressive Model

Generative Model

• 그럴듯한 이미지나 문장을 생성하는 모델 -> 하지만 그것이 전부는 아님
• Generator 외에 Discriminator까지 포함
  -> 학습 시켰을 때 이미지 생성 외에 이미지 구별도 가능(explicit model)

explicit model : 확률 값을 얻어낼 수 있는 모델
implicit model : 단순히 생성만 할 수 있는 모델(ex. VAE, GAN)

Learning a Generative Model

• dog 이미지가 있다고 가정
• Generative Model 활용 다음과 같은 probability distribution P(x) 학습
  • Generation : dog와 비슷한 새로운 sample $x_{new}$를 만듦(sampling)
  • Density estimation: p(x) 활용 dog와 비슷한지 구별(분류)
    -> anomaly detection에 활용 가능
  • Unsupervised representation learning : 강아지의 일반적인 특징 학습(feature learning)

Basic Discrete Distributions

유한한 data set에 대한 확률분포

• Bernoulli distribution : (biased) coin flip

  • 0 또는 1
  • p 값 한개로 확률분포 표현

• Categorical distribution : (biased) m-sided dice

  • 카테고리 m개 존재 -> 확률값 총합 1
  • m-1 개의 파라미터 필요

Categorical Distribution Example

• RGB joint distribution (One Pixel)
  • 경우의 수 : $256 * 256 * 256$
  • 파라미터 수 : $256 * 256 * 256 - 1$

• n개의 binary pixels
  • 경우의 수 : $2^n$
  • 파라미터 수 : $2^n$ - 1

파라미터 수가 너무 많다 -> 학습 어려워지므로 파라미터 수 감소시킬 필요 있음

Generative Model 파라미터 수 감소 방법

Structure Through Independence

• n개의 pixel들이 모두 independent 하다고 가정 -> 파라미터 전부 더하면 됨

  • 경우의 수 : $2^n$
  • 파라미터 수 : $n$
    -> 각 픽셀에 대해 파라미터 1개만 있으면 됨

• $2^n$개의 경우의 수를 단순히 n개로 표현
  -> 모든 픽셀이 independent하다는 가정은 말이 안된다.(표현할 수 있는 이미지가 적음)
  

Conditional Independence

Fully Dependent와 Independent의 중간
-> Conditional independence와 Chain rule을 잘 섞음

• Three important rules

  • Chain rule: n개의 joint distribution -> n개의 conditional distribution
    • independent 여부와 상관없이 항상 만족
    $p\left(x_{1}, \ldots, x_{n}\right)=p\left(x_{1}\right) p\left(x_{2} \mid x_{1}\right) p\left(x_{3} \mid x_{1}, x_{2}\right) \cdots p\left(x_{n} \mid x_{1}, \cdots, x_{n-1}\right)$

  • Bayes'rule:
    $p(x \mid y)=\frac{p(x, y)}{p(y)}=\frac{p(y \mid x) p(x)}{p(y)}$

  • Conditional independence: z가 주어졌을 때 x와 y가 independent
    -> x를 표현할 때 z가 주어지면 y는 없어도 됨(Conditional한 부분을 없애는 효과)
    $\text { If } x \perp y \mid z, \text { then } p(x \mid y, z)=p(x \mid z)$

• 단순 chain rule 활용 유도 방식

  • 파라미터 수 -> chain rule을 활용했을 뿐 달라진 게 없음
    • $p(x_1)$ : 1개
    • $p(x_2|x_1)$ : 2개 -> x1이 주어졌을 때 0 또는 1일 확률
    • $p(x_3|x_1, x_2)$ : 4개
      n에 대한 파라미터 수 : $2^n - 1$ -> 이전과 같음

• Markov assumption 활용 유도 방식

  • i+1 pixel은 i번째 pixel에만 dependent -> 나머지 pixel에는 independent
  • 다음과 같은 식으로 유도 -> independent 한 pixel 없애 줌
    $p\left(x_{1}, \ldots, x_{n}\right)=p\left(x_{1}\right) p\left(x_{2} \mid x_{1}\right) p\left(x_{3} \mid x_{2}\right) \cdots p\left(x_{n} \mid x_{n-1}\right)$
  • 파라미터 수 : $2n - 1$

  chain rule 적용 후 Markov assumption을 가하면, conditional independence를 활용해서
  $2^n - 1$ 개의 파라미터를 $2n - 1$ 개로 감소 가능

Auto-regressive Model

• Auto-regressive model은 conditional independency와 chain rule를 잘 활용한 모델

Example

• $28 * 28$ binary pixel을 가지고 있다고 가정
• 목표 : $28 * 28$ binary pixel에 대한 확률 분포 $p(x)$ 만드는 것
• $p(x)$ 표현 방법
  • joint distribution에 chain rule 적용 -> autoregressive model
    • 이전 pixel에 대해서만 dependent하다는 보장 없음
      -> i번째 pixel이 1부터 i-1번째 모든 픽셀에 대해 dependent 해도 Auto-regressive model
    • 어떤 식으로 conditional independence를 적용하느냐에 따라 모델 구조 달라짐

  • ordering이 중요
    • 이미지 각 pixel에 대한 순서를 매겨야 함
    • 순서를 어떻게 정하느냐에 따라 성능 달라짐
    • 이전 N개를 고려 할 때 Ar-N 모델이라고 부름

NADE : Neural Autoregressive Density Estimator

• NADE는 주어진 input에 대한 density를 계산할 수 있는 explicit model
• density 계산 방법
  • n개의 binary pixel이 주어졌다고 가정
  • joint distribution을 chain rule을 통해 conditional distribution으로 표현
    -> $p(x_i | x_{1:i-1})$ 각각을 independent하게 계산하여 확률 구함
  • continuous random variable일 경우 gaussian mixture 활용
    -> continuous한 distribution을 만듦

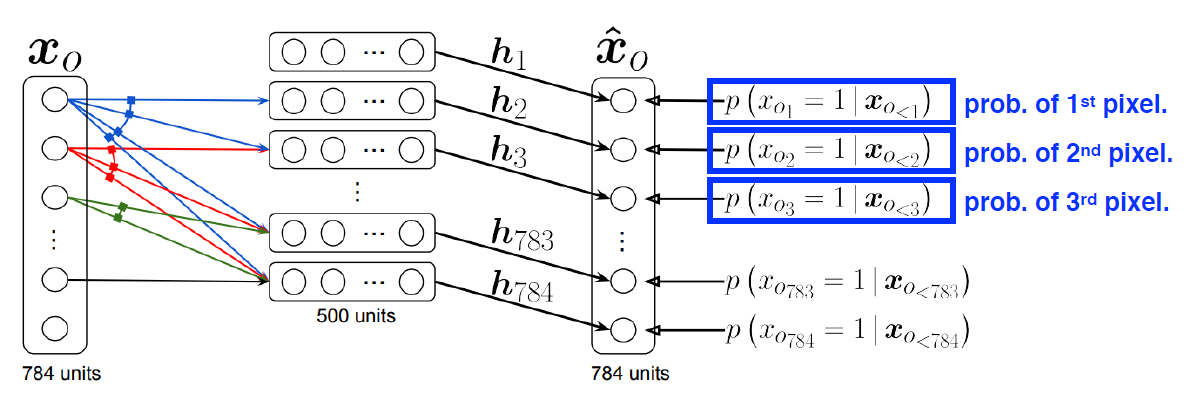
• i번째 픽셀을 1번째부터 i-1번째 픽셀에 대해 dependent하게 함
• neural network 입장에서는 입력 차원이 계속 달라짐 -> weight가 계속 커짐

Pixel RNN

• 이미지의 픽셀을 만들어 내기 위해 RNN 활용한 Auto-regressive model
• $n * n$ RGB image가 있을 때 i번째 pixel R, G, B 순차적으로 만듦

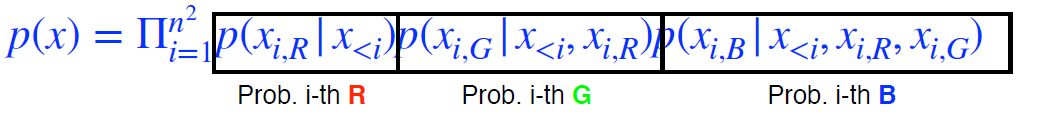
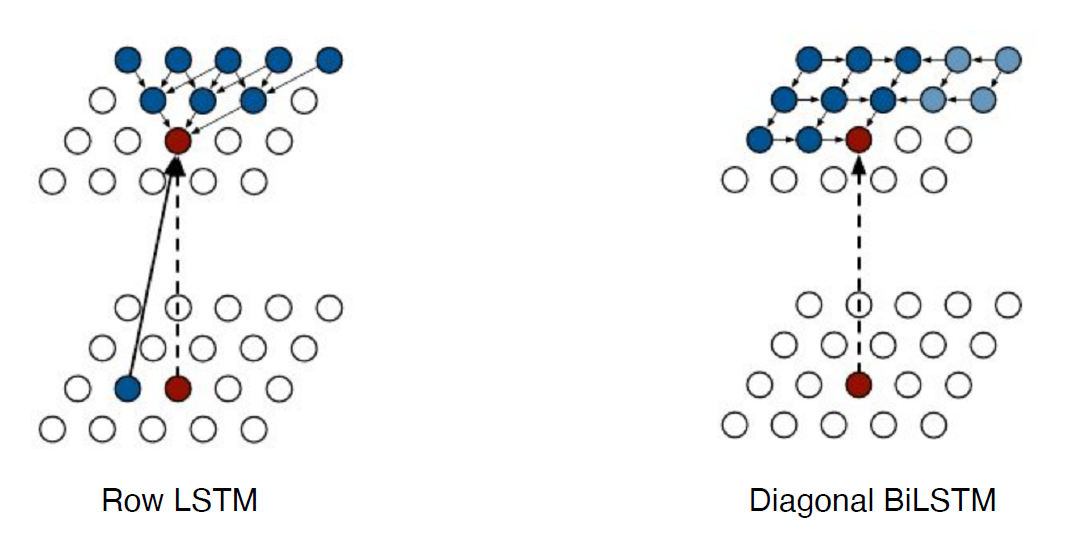
• chain ordering에 따라 다음과 같은 두 가지의 model architecture를 가짐
  • Row LSTM : i번째 픽셀을 만들 때 위쪽의 정보 활용
  • Diagonal BiLSTM : bidirectional LSTM 활용하되 ordering 기준 이전 정보 모두 활용