통계학

공부 내용

• 모수
• 확률분포 가정
• 최대가능도 추정법
• 확률분포의 거리

모수

• 통계적 모델링은 적절한 가정 위에서 확률분포를 추정(inference)하는 것이 목표
• 그러나 유한한 개수의 데이터만 관찰해서 모집단의 분포를 정확하게 알아내는 것을 불가능
  • 근사적으로 확률분포를 추정해야 함

모수적 방법론 vs 비모수적 방법론

• 데이터가 특정 확률분포를 따른다고 선험적으로(a priori) 가정한 후 그 분포를 결정하는 모수를 추정하는 방법을 모수적(parametric) 방법론이라 함
• 반면 특정 확률분포를 가정하지 않고 데이터에 따라 모델의 구조 및 모수의 개수가 유연하게 바뀌면 비모수(nonparametric) 방법론이라 함
  • 비모수 방법론이라고 모수를 사용하지 않는것이 아님!!
• 기계학습의 많은 방법론은 비모수 방법론에 속함

확률분포 가정

• 데이터가 2개의 값(0 또는 1)만 가지는 경우 : 베르누이분포
• 데이터가 n개의 이산적인 값을 가지는 경우 : 카테고리분포
• 데이터가 [0,1] 사이에서 값을 가지는 경우 : 베타분포
• 데이터가 0 이상의 값을 가지는 경우 : 감마분포, 로그정규분포 등
• 데이터가 실수 전체에서 값을 가지는 경우 : 정규분포, 라플라스분포 등
• 데이터를 생성하는 원리를 먼저 고려해서 확률분포를 가정해야 한다.

표집분포

• 통계량(표본평균, 표본분산)의 확률분포를 표집분포(sampling distribution)라 부르며, 특히 표본평균의 표집분포는 표본 개수 $N$이 커질수록 정규분포를 따르게 된다.
  • 이를 중심극한정리(Central Limit Theorem)이라 부르며, 모집단의 분포가 정규분포를 따르지 않아도 성립
  • 표본분포는 정규분포를 따르지 않을 수도 있음!!

최대가능도 추정법

• 최대가능도 추정법(maximum likelihood estimation, MLE)는 이론적으로 가장 가능성이 높은 모수를 추정하는 방법 중 하나

  

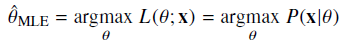
• 데이터 집합 $X$가 독립적으로 추출되었을 경우 로그가능도를 최적화

  

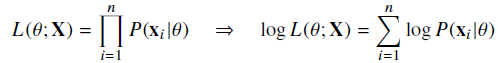
로그가능도 사용 이유

• 데이터의 숫자가 수억 단위가 된다면 컴퓨터의 정확도로 가능도를 계산하는 것이 불가능
• 데이터가 독립일 경우, 로그를 사용하면 가능도의 곱셈을 로그가능도의 덧셈으로 바꿀 수 있기 때문에 컴퓨터 연산이 가능해짐
• 경사하강법으로 가능도를 최적화할 때, 로그 가능도를 사용하면 연산량을 $O(n^2)$에서 $O(n)$으로 줄일 수 있음
• 대개의 손실함수의 경우 경사하강법을 사용하므로 음의 로그가능도(negative log-likelihood)를 최적화

확률분포의 거리

• 기계학습에서 사용되는 손실함수들은 모델이 학습하는 확률분포와 데이터에서 관찰되는 확률분포의 거리를 통해 유도
• 데이터 공간에 데이터에서 관찰되는 확률분포 $P(x)$, 모델이 학습하는 확률분포 $$Q(x)가 있을 경우 두 확률분포 사이의 거리(distance)를 계산할 때 다음과 같은 함수들을 이용
  • 총변동 거리 (Total Variation Distance, TV)
  • 쿨백-라이블러 발산 (Kullback-Leibler Divergence, KL)
  • 바슈타인 거리 (Wasserstein Distance)