확률론

공부 내용

• 확률분포
• 조건부확률
• 기댓값
• 몬테카를로 샘플링

확률분포

• 확률분포는 데이터의 초상화
• 데이터공간을 $X \times Y$ 라 표기하고 $D$는 데이터공간에서 데이터를 추출하는 분포

확률변수

• 확률분포 $D$에 따라 이산형(discrete)과 연속형(continuous) 확률변수로 구분

  • 이산형 확률변수는 확률변수가 가질 수 있는 경우의 수를 모두 고려하여 확률을 더해서 모델링

  

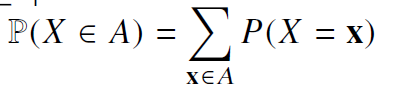
  • 연속형 확률변수는 데이터 공간에 정의된 확률변수의 밀도(density) 위에서의 적분을 통해 모델링

  

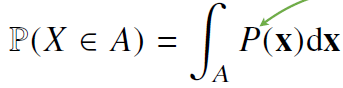
주변확률분포

• $P(x)$는 입력 $x$에 대한 주변확률 분포로 $y$에 대한 정보를 주진 않음

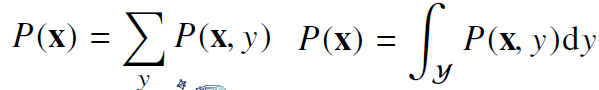
조건부확률분포

• 조건부확률분포 $P(X|y)$는 데이터 공간에서 입력 $x$와 출력 $y$ 사이의 관계를 모델링
  • $P(X|y)$는 특정 클래스가 주어진 조건에서 데이터의 확률분포를 보여줌

조건부확률

• 조건부확률 $P(y|x)$는 입력변수 $x$에 대해 정답이 $y$일 확률
• 분류 문제에서 softmax는 데이터 x로부터 추출된 특징패턴과 가중치행렬을 통해 조건부확률을 계산
• 회귀 문제의 경우 조건부기대값을 추정
• 딥러닝은 다층신경망을 사용하여 데이터로부터 특징패턴을 추출
  • 특징패턴을 학습하기 위해 어떤 손실함수를 사용할지는 기계학습 문제와 모델에 의해 결정

기대값

• 확률분포가 주어지면 데이터를 분석하는데 사용 가능한 여러 종류의 통계적 범함수(statistical functional)를 계산할 수 있음
• 기대값(expectiation)은 데이터를 대표하는 통계량이면서 동시에 확률분포를 통해 다른 통계적 범함수를 계산하는데 사용
• 기대값을 이용해 분산, 첨도, 공분산 등 여러 통계량을 게산할 수 있음

몬테카를로 샘플링

• 기계학습의 많은 문제들은 확률분포를 명시적으로 모르는 경우가 대부분
• 확률 분포를 모를 때 데이터를 이용하여 기대값을 계산하려면 몬테카를로(Monte Carlo) 샘플링 방법을 사용해야 함
• 몬테카를로 샘플링은 독립추출만 보장된다면 대수의 법칙(law of large number)에 의해 수렴성을 보장
• 몬테카를로 샘플링은 기계학습에서 매우 다양하게 응용되는 방법

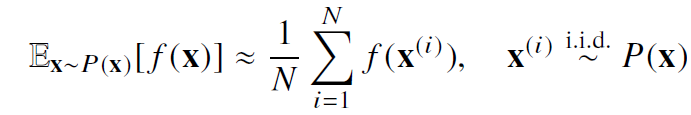
대수의 법칙

• 큰 모집단에서 무작위로 뽑은 표본의 평균이 전체 모집단의 평균과 가까울 가능성이 높다는 통계와 확률 분야의 기본 개념