📒손실함수
- 모델의 출력값과 실제 데이터의 정답 사이의 오차를 계산하는 함수
- AI 모델을 학습한다는 것 = 주어진 데이터에 대한 정답에 근사한 예측을 할 수 있는 모델을 만드는 것
-> 손실을 최대한 작은 값으로 줄이는 것이 AI 모델 학습의 목표
💡분류 (Classification)
- 주어진 데이터가 어떤 범주에 속하는지 판단하는 태스크
- Logit : 표준화되지 않은 날 것 그대로의 모델 예측값
- 확률값(probability) : logit에 추가 연산을 가하여 [0, 1] 사이의 확률값으로 나타낸 예측값
Cross entropy
-
분류에 쓰이는 가장 대표적인 손실 함수
-
이진 분류

-
다중 분류
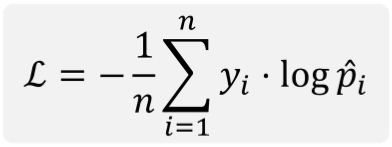
💡회귀 (Regression)
- 범주가 아닌 연속적인 수치를 예측하는 태스크
MSE (Mean Squared Error)

MAE (Mean Absolute Error)

📒활성 함수
- 각 뉴런의 출력을 비선형으로 변환하여 복잡한 관계를 학습할 수 있도록 함
ReLU (Rectified Linear Unit)
- 0보다 작은 입력은 0으로, 0보다 큰 입력은 그대로 출력
- 장점 : 계산이 간단하고, Vanishing Gradient 문제를 해결
- 단점 : 0 이하로 학습이 멈출 수 있는 "Dying ReLU" 문제 발생 가능
Sigmoid
- 출력 값을 0과 1사이로 제한
- 주로 이진 분류 문제에서 사용
- 출력이 확률처럼 해석됨
- 문제점 : 입력이 너무 크거나 작으면, 경사 하강법에서 기울기가 거의 0이 되어 학습이 어려워짐
Tanh
- 출력 값을 -1과 1 사이로 제한
- Sigmoid와 유사하지만, 출력 범위가 넓어지므로 더 강한 비선형성을 제공
- Vanishing Gradient 문제
Leaky ReLU
- ReLU와 유사하지만, 0 이하의 입력에 대해서도 작은 기울기를 가짐 (보통 0.01)
- Dying ReLU 문제를 해결하기 위한 변형
Swish
- ReLU + Sigmoid
- 출력이 부드럽게 변화
