✅ 문제
무한히 큰 배열에 다음과 같이 분수들이 적혀있다.
이와 같이 나열된 분수들을 1/1 -> 1/2 -> 2/1 -> 3/1 -> 2/2 -> … 과 같은 지그재그 순서로 차례대로 1번, 2번, 3번, 4번, 5번, … 분수라고 하자.
X가 주어졌을 때, X번째 분수를 구하는 프로그램을 작성하시오.
✅ 입력
첫째 줄에 X(1 ≤ X ≤ 10,000,000)가 주어진다.
✅ 출력
첫째 줄에 분수를 출력한다.
✅ 예제 1
▼ 입력
14▼ 출력
2/4풀이
이 문제 역시 규칙을 도출하여 풀어야 한다. 처음에는 배열을 통해 풀려고 했으나, 배열의 크기 설정 및 인덱스 문제로 인해 배보단 배꼽이 커지는 문제가 발생해서.. 다른 방법을 생각해야 했다.
문제에 주어진 그림을 다시 보자.
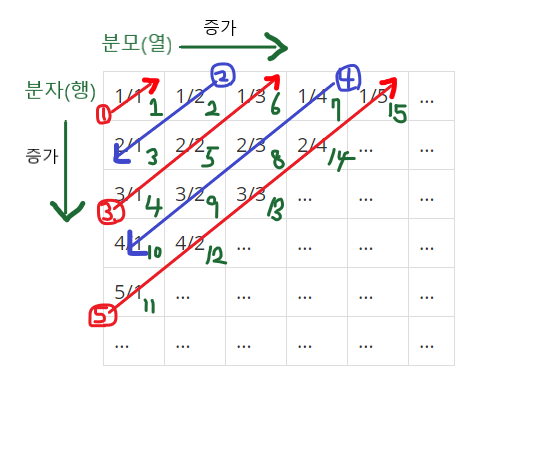
-
한 개의 분수는
분자/분모로 이루어져 있다. 분자는 아래쪽(y축)으로 갈수록 값이 증가하므로 행으로, 분모는 오른쪽(x축)으로 갈수록 값이 증가하므로 열로 사용한다. -
우상향의 경우
분자는 감소하고분모는 증가한다. 예를 들어 ③번 라인을 살펴보면, 분수는 차례대로3/1,2/2,1/3이 존재한다. 이를 분자와 분모로 각각 분류하면,분자는 3, 2, 1로 감소,분모는 차례대로 1, 2, 3으로 증가한다는 것을 알 수 있다. -
반면에 좌하향의 경우
분자는 증가하고분모는 감소한다. 예를 들어 ④번 라인을 살펴보면, 분수는 차례대로1/4,2/3,3/2,4/1이 존재한다. 이를 분자와 분모로 각각 분류하면,분자는 1, 2, 3, 4로 증가,분모는 차례대로 4, 3, 2, 1로 감소한다는 것을 알 수 있다. -
각 라인을 이루는 분수의 갯수는 라인의 순서와 일치한다. 그림을 보면, ①번 라인에는
1/11개, ②번 라인에는1/2,2/12개, ③번 라인에는3/1,2/2,1/33개, ... 이런식으로 일치한다는 것을 확인할 수 있다.
여기서 우상향 라인의 경우 ①, ③, ⑤, ... 로 홀수번째 라인들로 이루어져 있음을 알 수 있다. 좌하향 라인의 경우 ②, ④, ⑥, ... 으로 짝수번째 라인들로 이루어져 있음을 알 수 있다.
규칙을 도출했으니 다시 돌아와서 문제를 풀어보자. 내가 생각한 방법은 다음과 같다.
-
찾으려는 분수(이하
x)를 찾았는지 여부를 표시하는 변수(이하bool)를 하나 선언하고, 아직 못 찾은 상태를 나타내는 값으로 초기화 한다.bool을 이용하여 반복문을 실행한다. -
우상향(홀수)라인의 경우
분모를 라인의 시작값으로 초기화 한 뒤, 라인이 종료할 때 까지분자는 감소,분모는 증가하고, 좌하향(짝수)라인의 경우는분모를 라인의 마지막값으로 초기화, 라인이 종료할 때 까지분자는 증가,분모는 감소하도록 한다.
동시에 몇 번째 분수인지 카운트 한다. 만약x를 찾았다면 분수를 찾았음을 표시하고 모든 루프를 종료한다. -
한 라인의
분자와분모의 증감이 정상적으로 종료되었다면 아직x를 못 찾은 상태이므로, 다음 라인으로 이동하여 반복문을 처음부터 다시 실행한다.
이와 같은 방법으로 작성한 코드는 다음과 같다.
💻 코드
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int x = scanner.nextInt();
scanner.close();
int line = 1; // 행 번호
int no = 0; // 분수 순서
int top = 0, bottom = 0; // 각각 분자, 분모
// x번째 분수 찾았는지 여부 표시
boolean bool = true; // true: 아직 못찾음, false: 찾음
while(bool) { // 아직 찾으려는 분수 발견 못했다면
if(line % 2 == 1) { // 홀수 행 일 때(분자↓, 분모↑)
bottom = 0; // 분모 초기화
for(top=line; top>=1; top--) { // 분자는 감소
bottom++; // 분모는 증가
no++; // 몇 번째 분수인지 표시
if(no == x) { // 현재 분수가 x번째 분수라면
bool = false; // 분수를 찾았음을 표시하고
break; // 루프 종료
}
} // -------- for문 끝
} // ----------- if문 끝
else { // 짝수 행 일 때(분자↑, 분모↓)
bottom = line+1; // 분모 초기화
for(top=1; top<=line; top++) { // 분자는 증가
bottom--; // 분모는 감소
no++;
if(no == x) {
bool = false;
break;
}
} // -------- for문 끝
} // ----------- if문 끝
line++; // 한 행 종료하면 행 증가
} // --------------- while문 끝
System.out.println(top + "/" + bottom);
}
}