[BOJ] 2292 벌집 (JAVA)

✅ 문제

위의 그림과 같이 육각형으로 이루어진 벌집이 있다. 그림에서 보는 바와 같이 중앙의 방 1부터 시작해서 이웃하는 방에 돌아가면서 1씩 증가하는 번호를 주소로 매길 수 있다.

숫자 N이 주어졌을 때, 벌집의 중앙 1에서 N번 방까지 최소 개수의 방을 지나서 갈 때 몇 개의 방을 지나가는지(시작과 끝을 포함하여)를 계산하는 프로그램을 작성하시오.

예를 들면, 13까지는 3개, 58까지는 5개를 지난다.

✅ 입력

첫째 줄에 N(1 ≤ N ≤ 1,000,000,000)이 주어진다.

✅ 출력

입력으로 주어진 방까지 최소 개수의 방을 지나서 갈 때 몇 개의 방을 지나는지 출력한다.

✅ 예제 1

▼ 입력

13

▼ 출력

3

---

풀이

어떻게 풀어야 하나 고민하다 보니 나름의 규칙이 있다는 것을 발견했다.

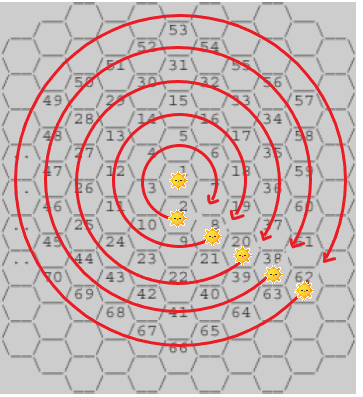
위의 그림을 살펴보면, 중앙부터 시작하여 시계 방향으로 원을 그리며 방을 감싸고 있다는 것을 알 수 있다. 문제에서 요구하는 것은 이동할 때 필요한 방의 최소 개수(이하 roomCnt)이다. 이것을 구하기 위해서는 각 원에 포함되는 방의 개수 및 번호를 알아야 한다.

좀 더 자세하게 풀이해보자면, 1에서 바로 이동할 수 있는 방들의 그룹을 x라고 하고, 여기에는 2, 3, 4, 5, 6, 7 이 있을 수 있다. 예를 들어 1에서 4로 이동한다고 하면, 이 때는 roomCnt가 1과 4 총 2개가 되는 것이다.

그 다음 원(이하 y)으로 이동하기 위해서는 x에 해당하는 방들이 모두 있어야 가능하다. 왜냐고? 문제를 다시 읽어보자.

중앙의 방 1부터 시작해서 이웃하는 방에 돌아가면서 1씩 증가하는 번호를 주소로 매길 수 있다.

즉, x가 완전히 채워진 상태가 아니라면 y로 이동할 수가 없다는 소리다.

y를 이룰 수 있는 방들은 8, 9, 10, ... , 18, 19로, x에서 최소한의 움직임으로 y로 이동하고 싶다면 13 혹은 14로 이동하면 된다. 13으로 이동한다고 하면 roomCnt는 1, 4, 13 총 3개가 된다.

이동하는 방식을 알아냈으니 이젠 규칙을 도출하여 코드를 짜야 한다. 다음 그림을 보자.

각 원의 시작점을 기준으로 방의 최소 개수는 하나씩 증가한다. 1을 제외한 나머지 시작점들은 두 수의 차가 6의 배수 이고, 이 두 수의 차의 차를 구하면 6이 나온다. 두 수의 차의 차는 등차수열이라고 할 수 있으며, 이는 규칙적으로 증가하는 수라는 것이다. 이를 이용하여 규칙을 세워보면 다음과 같다.

1. 방 번호(이하 no)가 1일 경우는 바로 이동할 때 필요한 방의 최소 개수(이하 roomCnt)를 1로, 2부터는 반복문을 통하여 도출한다.
2. 반복문을 실행하며 문두에 다음 원으로 이동시 한 원을 채우는 방의 갯수(이하 moveEndCnt)를 구한 뒤 조건문을 통해 현재까지 이동한 방의 갯수(이하 moveEachCnt)와 moveEndCnt가 같은지 판별한다. 만약 같다면 다음 원으로 이동해야 하므로 roomCnt를 하나 증가시키고 moveEachCnt를 1로 초기화 한다. 같지 않다면 아직 다음 원으로 이동하지 않는다는 뜻이기 때문에 moveEachCnt만 증가시킨다.
   
   

설명이 잘 이해가 가지 않는다면 아래의 코드를 보자. 좀 더 쉽게 이해할 수 있을 것이다.

💻 코드

import java.util.Scanner;

public class Main {
	public static void main(String[] args) {
		Scanner scanner = new Scanner(System.in);
		long no = scanner.nextInt();
		scanner.close();
		
		int roomCnt;	// 거쳐가야하는 최소 방의 개수
		
		if(no == 1)	// 방 번호 1일 경우
			roomCnt = 1;
		else	// 방 번호가 2번부터는
			roomCnt = bee(no);

		System.out.println(roomCnt);
	}
	
	public static int bee(long no) {
		int roomCnt = 2;	// 방 번호가 2부터 시작하기 때문에 방 개수도 2부터
		int moveEachCnt = 1;	// 이동한 방의 갯수 카운트
		int moveEndCnt;	// 한 바퀴를 채우기 위해 필요한 방의 개수
		
		for(long i=2; i<=no; i++) {	// 2번 방부터
			moveEndCnt = 6 * (roomCnt-1) + 1;  // 6 * (cnt-1) → 6, 12, 18, ...
							   // 다음 바퀴를 채워야 하므로 1을 더해줌
			if(moveEachCnt == moveEndCnt) { // 이동한 방의 갯수와 한 바퀴를 채워야 할 방의 갯수가 같다면
				roomCnt++;  // 최소 필요 방 개수 증가
				moveEachCnt = 1;  // 이동한 방의 개수 초기화
			}
			moveEachCnt++;	// 이동한 방의 개수 증가
		}
		
		return roomCnt;
	}
}