[9251] LCS

👉 9251 LCS

[정답 코드]

import sys
input = sys.stdin.readline

def find_longest(memo_max, j):
    longest = 0
    for i in range(j):
        if longest < memo_max[i]: longest = memo_max[i]
    return longest

f_str = input().rstrip()
s_str = input().rstrip()
f_len = len(f_str)
s_len = len(s_str)
matrix = [[0 for col in range(f_len + 1)] for row in range(s_len + 1)]
memo_max = [0] * (f_len + 1)
ans = 0

for i in range(1, s_len + 1):
    for j in range(1, f_len + 1):
        if f_str[j - 1] == s_str[i - 1]:
            longest = find_longest(memo_max, j)
            matrix[i][j] = longest + 1
            if ans < matrix[i][j]: ans = matrix[i][j]
    for j in range(1, f_len + 1):
        if memo_max[j] < matrix[i][j]:
            memo_max[j] = matrix[i][j]
print(ans)

[풀이]

👉 LCS(Longest Common Substring)

알고리즘 수업 때 배웠던 LCS(Longest Common Substring)을 토대로 시작했다. 이는 최장 공통 문자열로, 문제에서 요구하는 부분 문자열이 아닌 한번에 이어져있는 문자열만 가능하다.
pseudocode는 다음과 같다.

if i = 0 or j = 0 
	matrix[i][j] <= 0
else if string_A[i] = string_B[j]
	matrix[i][j] <= matrix[i - 1][j - 1] + 1
else
	matrix[i][j] <= 0

👉 LCS(Longest Common Subsequence)

Longest Common Substring과 다르게 부분 문자열이 가능하다. (문자 사이를 건너뛰는 것이 가능) 그래서 내가 처음 생각한 알고리즘은 다음과 같다.
1. 두 문자열을 한 글자씩 비교한다.
2. 두 문자가 다르다면 0 표시한다.
3. 두 문자가 같다면 matrix[0][0] ~ matrix[i - 1][j - 1] 중 최댓값에 1을 더한 값을 표시한다.
4. 위 과정을 반복한다.

두 문자가 같은 상황이 오면 그 바로 직전의 Longest Common Subsequence에 1을 더해주면 되기 때문에 matrix[i - 1][j - 1]까지의 값들 중 최댓값을 구해야겠다고 생각했다.

하지만 최댓값을 구하는 데 for문을 사용해버리면 시간복잡도가 O(N^4)로 되기 때문에, memoization을 또 사용하였다. 즉, memoization이 최댓값과 matrix에 두번 사용된 것이다.

• 열 길이에 맞게 1차원 배열을 생성한 후, 각 열을 검사한 뒤 열에 해당하는 최댓값을 배열에 저장하였다. 즉, matrix[i - 1][j - 1]까지의 값들 중 최댓값은 memo_max[j - 1] 까지의 값들 중 최댓값이 되는 것이다.
• (오류 해결) 처음엔 각 열을 검사한 뒤가 아닌 한 글자씩 비교할 때마다 최댓값을 갱신하였었다. 이 때문에 matrix[i - 1][j - 1]까지가 아닌 matrix[i][j - 1]까지의 최댓값이 반환되었다.

---

내가 생각한 알고리즘을 더욱 간단하고 편리하게 만든 것이 원래의 LCS(Longest Common Subseqence) Algorithm이다.
pseudocode는 다음과 같다.

if i = 0 or j = 0 
	matrix[i][j] <= 0
else if string_A[i] = string_B[j]
	matrix[i][j] <= matrix[i - 1][j - 1] + 1
else
	matrix[i][j] <= the maximum of matrix[i][j - 1] and matrix[j - 1][i]

✔ matrix[i][j - 1]와 matrix[j - 1][i]

최대 공통 부분수열은 한 글자씩 검사할때마다 계속해서 유지된다. 즉, 검사하기 이전의 값도 최대 공통 부분 수열이라는 것이다. matrix[i][j - 1]와 matrix[j - 1][i]가 현재 문자를 비교하기 직전의 최대 공통 부분 수열이다.

[구현 코드]

import sys
input = sys.stdin.readline

f_str = input().rstrip()
s_str = input().rstrip()
f_len = len(f_str)
s_len = len(s_str)
matrix = [[0 for col in range(f_len + 1)] for row in range(s_len + 1)]

for i in range(1, s_len + 1):
    for j in range(1, f_len + 1):
        if f_str[j - 1] == s_str[i - 1]:
            matrix[i][j] = matrix[i - 1][j - 1] + 1
        elif matrix[i][j - 1] > matrix[i - 1][j]:
            matrix[i][j] = matrix[i][j - 1]
        else:
            matrix[i][j] = matrix[i - 1][j]
print(matrix[s_len][f_len])

최대 공통 부분 수열의 길이 뿐만 아니라, 전체 수열까지 구하고 싶을 때는 원래의 알고리즘 방식이 더 유용할 것 같다. (수열을 역으로 찾아나가는 과정이 단순함) 실제로 시간도 많이 단축된다.

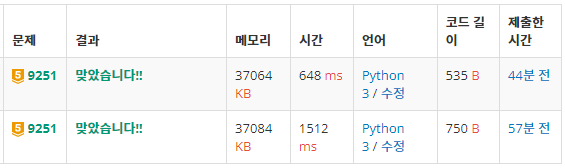
LCS에 대한 설명은 아래 링크를 바탕으로 작성하였다.
LCS 알고리즘

[적용 자료구조 및 알고리즘]

• Dynamic Programming