👉 9663 N-Queen
python으로 풀면 시간초과문제가 발생하기 때문에, C/C++로 푸는 것이 더 용이하다고 한다.(아래의 코드는 pypy로 제출하면 통과된다)
[정답 코드]
import sys
def is_promising(row):
global board
for i in range(row):
if board[i] == board[row] or row - i == abs(board[row] - board[i]):
return False
return True
def n_queen(row):
global board
global ans
if row == len(board):
ans += 1
else:
for i in range(len(board)):
if visited[i]: continue
board[row] = i
if is_promising(row):
visited[i] = True
n_queen(row + 1)
visited[i] = False
n = int(sys.stdin.readline())
board = [-1] * n
visited = [False] * n
ans = 0
n_queen(0)
print(ans)[풀이]
- is_promising 함수는 board의 row행, i열에 queen을 두었을 시 n_queen 조건에 부합하는 지 체크해주는 함수이다. (pruning 과정이다)
- visited는 pruning 하기 전 같은 열에 queen이 있는지 미리 파악하기 위한 장치이다. 즉, visited를 사용함으로써 is_promising 함수의 if문에서
board[i] == board[row]은 없어도 된다.(visited를 사용하지 않을 경우 pypy로 제출해도 시간초과가 발생한다.)
[정리]
처음 작성한 코드는 2차원 배열을 만들어, 위와 똑같은 구조로 검사하는 방식이었다.(당연히 시간 초과) 시간을 줄이는 순차적 방법은 다음과 같다.
1. 2차원 배열을 1차원 배열로 줄인다. n-queen은 정사각형에서만 진행되기 때문에 1차원 배열의 index를 행으로 취급하는 것이다.
2. visited를 만들어 pruning 하기 전 같은 열에 queen이 있는지를 미리 파악한다. (is_promising 함수 호출 횟수가 적어짐)
[적용 자료구조 및 알고리즘]
- Brute Force & Backtracking
[더 나은 아이디어]
위의 정리 2에서 더 나아가 is_promising 함수 호출 횟수를 더 줄이는 방식이 있다. visited는 해당 열에 대해 queen의 중복이 발생하는지의 여부를 파악하는데, 대각선에 대한 것도 같은 방식으로 구현하는 것이다. 즉, is_promising 호출 자체가 필요없다.
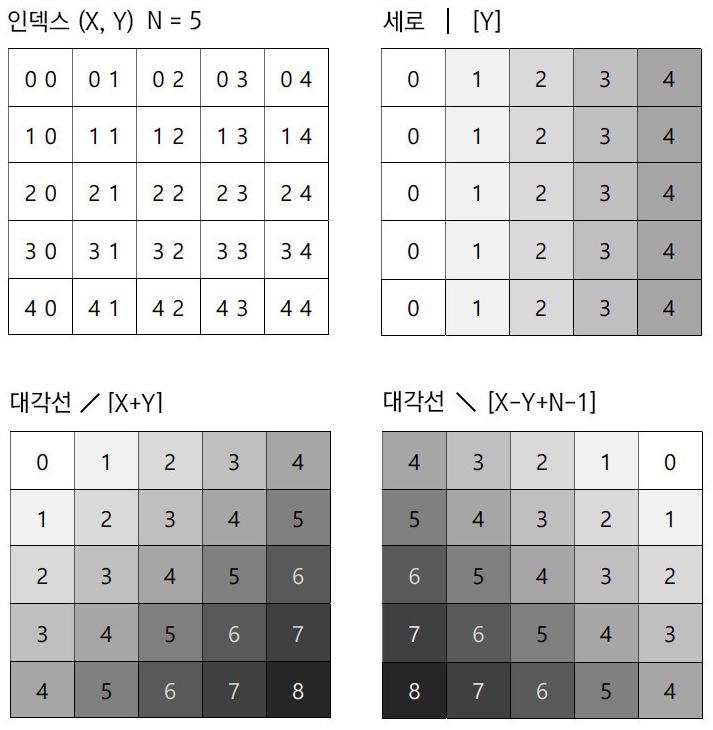
n, ans = int(input()), 0
a, b, c = [False]*n, [False]*(2*n-1), [False]*(2*n-1)
def solve(i):
global ans
if i == n:
ans += 1
return
for j in range(n):
if not (a[j] or b[i+j] or c[i-j+n-1]):
a[j] = b[i+j] = c[i-j+n-1] = True
solve(i+1)
a[j] = b[i+j] = c[i-j+n-1] = False
solve(0)
print(ans)
확실히 시간이 많이 준다.(두 번째 제출 코드는 첫 번째 코드의 is_promising의 if문에서 board[i] == board[row]을 없앤 코드이다.)
N-Queen 에서 자세한 설명과 코드를 볼 수 있다.
