[Statistics] Markov Chain Monte Carlo & Gibbs Sampling

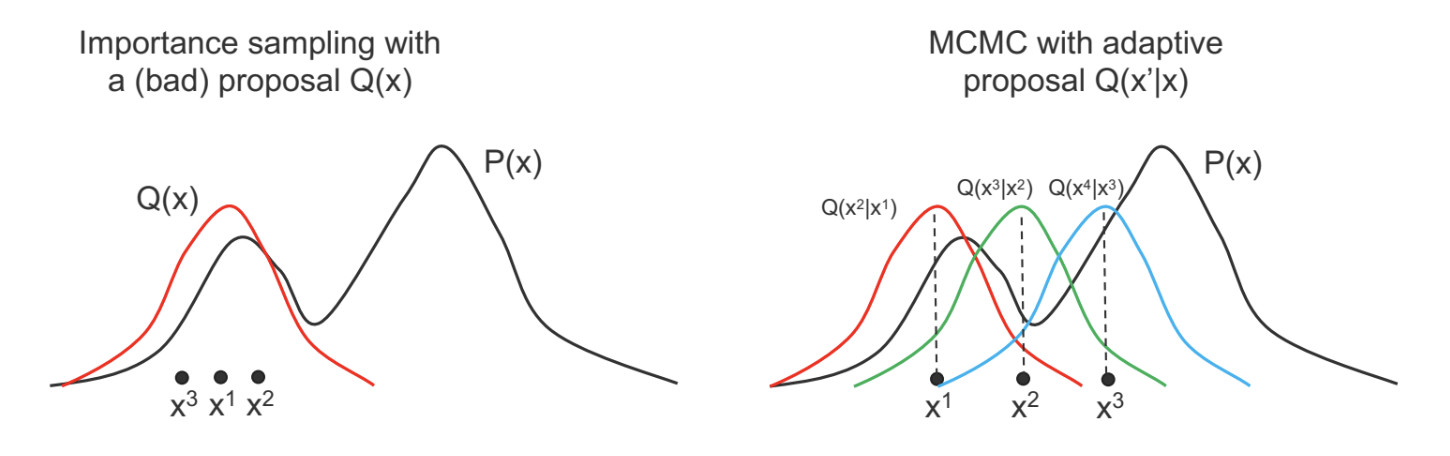
출처 : Lecture 14: Approximate Inference: Markov Chain Monte Carlo

[Statistics] Gibbs Entropy, Gibbs Distribution
해당 글에 이어서 작성. 먼저 Markov Chain Monte Carlo(MCMC)의 개념을 정리하고 Gibbs Sampling에 대해서 설명한다.

1. Markov Chain Monte Carlo(MCMC)

1.1 마르코프 연쇄의 개념

MCMC (Markov Chain Monte Carlo)는 특정 확률 분포 $P(x)$에서 직접 샘플을 생성하기 어려운 경우, 분포를 근사하여 샘플을 생성하는 방법이다.

왜 전체 분포에서 직접 샘플링 하지 않을까? 여러 이유가 있다.

• 우선 다변량, 고차원에서 확률 분포는 직접 샘플링하기 어려운 측면이 있다.
• 전체 분포를 모르고 조건부 분포만을 알고 있을 가능성도 있다.
• Gibbs distribution에서 정규화 상수(Partition Function)를 현실적으로 계산하기 거의 불가능 한 경우도 있다.

이러한 상황에서 MCMC는 유용한 도구가 된다. 한편, MCMC는 2가지 원리에 기초를 두고 있다.

• 마르코프 연쇄 (Markov Chain) : 현재 상태에서 다음 상태로 전이할 확률이 오직 현재 상태에만 의존하는 확률 과정이다.
  $P(X_{t+1} \mid X_t, X_{t-1}, \dots) = P(X_{t+1} \mid X_t)$
• 몬테 카를로 샘플링 (Monte Carlo Sampling) :난수를 생성하여 확률 분포를 근사하거나 수치적 기대값을 추정하는 방식이다.

결국, MCMC는 마르코프 연쇄를 구성하여 그 연쇄가 우리가 원하는 분포에 수렴하도록 설계하고, 충분한 반복 후에 얻은 샘플들을 통해 분포를 근사하는 방법이다.

1.2 마르코프 연쇄의 성질

MCMC가 효과적으로 작동하려면, 사용되는 마르코프 연쇄가 다음 조건들을 만족해야 한다.

• Stationarity (불변 분포) : 시간에 따라 분포가 바뀌지 않는 상태를 가진다. $\pi(x') = \sum_x \pi(x) P(x \to x')$
• Irreducibility (이행성) :어떤 상태에서 시작해도 다른 모든 상태로 도달할 수 있어야 한다.
• Aperiodicity (비주기성) : 일정한 주기로만 상태를 방문하지 않아야 한다.
• Detailed Balance (상세 균형 조건) : 두 상태 사이의 전이 확률이 쌍방향으로 균형을 이루는 경우이다.
  $\pi(x) P(x \to x') = \pi(x') P(x' \to x)$

이러한 조건이 만족되면, 마르코프 연쇄는 시간이 지남에 따라 우리가 원하는 분포 $\pi(x)$로 수렴하게 된다.

1.3 마르코프 연쇄와 Gibbs Sampling의 관계

MCMC는 위의 성질들을 따르는 확률적 샘플링 방법들의 총칭이다. 그중에서도 Gibbs Sampling은 MCMC의 특수한 형태로, 각 변수의 조건부 분포를 사용하여 샘플을 생성하는 방식이다.

즉, 복잡한 전체 결합 분포를 직접 샘플링하지 않고, 각 변수의 조건부 분포에서 순차적으로 샘플링함으로써 전체 분포를 근사한다.

2. Gibbs Sampling

2.1 Gibbs Sampling의 기본 개념

Gibbs Sampling는 조건부 분포를 알고 있는 경우의 MCMC이다. 이를 알기 위해선 다변량 분포에서 조건부 분포를 알아야한다. 그리고 각 조건부 분포에서는 하나의 변수만 샘플링하는데도, 전체 결합 분포의 샘플을 근사할 수 있는 이론적 이유가 필요하다. 이는 마르코프 균형 조건을 만족하고, 이는 마르코프 연쇄 성질을 보장한다.

각 조건부 분포는 하나의 변수만을 샘플링하지만, 전체 결합 분포를 근사할 수 있다. 이론적으로 이는 마르코프 균형 조건(Markov Equilibrium Condition)을 만족하며, 따라서 마르코프 연쇄 성질을 보장한다.

2.2 Gibbs Sampling 알고리즘

• 초기값 $X^{(0)} = (X_1^{(0)}, X_2^{(0)}, ..., X_d^{(0)})$ 설정

• 초기값을 랜덤하게 설정

• 각 변수별 조건부 분포를 기반으로 샘플링

  • 각 변수 $X_i$에 대해 순차적으로 업데이트
  • (예시 : 이변량 정규 분포의 경우)
    $X_1^{(t+1)} \sim P(X_1 \mid X_2^{(t)})$
    $X_2^{(t+1)} \sim P(X_2 \mid X_1^{(t+1)})$

• 충분한 반복 후 수렴한 샘플을 사용하여 전체 분포를 근사