시간 복잡도
빅오표기법
시간 복잡도
: 입력 크기에 대해 어떠한 알고리즘이 실행되는 데 걸리는 시간
주요 로직의 반복 횟수를 중점으로 측정된다.
for (int i = 0; i < 10; i++) {
for (int j = 0; j < n; j++) {
for (int k = 0; k < n; k++) {
if (true) cout << k << '\n';
}
}
}
for (int i = 0; i < n; i++) {
if (true) cout << i << '\n';
}
'입력 크기 n'의 모든 입력에 대한 알고리즘에 필요한 시간이 10n^2+n
위 코드의 시간 복잡도를 빅오 표기법으로 나타내면 이 된다.
-> '가장 영향을 많이 끼치는' 항의 상수 인자를 빼고 나머지 항을 없앰
시간 복잡도의 존재 이유
효율적인 코드로 개선하는 데 쓰이는 척도가 된다.
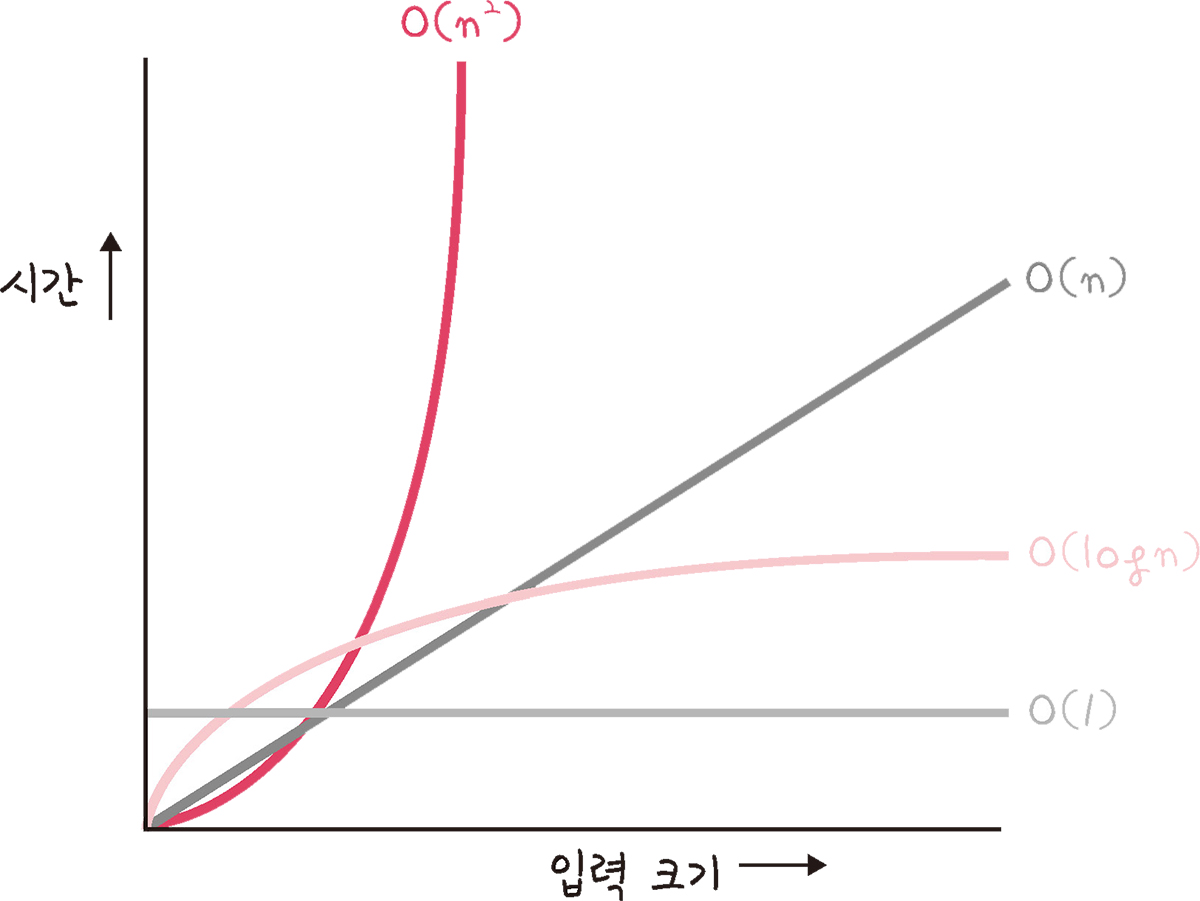보다는 , 보다는 을 지향해야 함
공간 복잡도
공간 복잡도
: 프로그램을 실행시켰을 때 필요로 하는 자원 공간의 양
자료 구조에서의 시간 복잡도
자료 구조를 쓸 때는 시간 복잡도를 잘 생각해야 한다.
자료 구조의 평균 시간 복잡도
| 자료구조 | 접근 | 탐색 | 삽입 | 삭제 |
|---|---|---|---|---|
| 배열(array) | O(1) | O(n) | O(n) | O(n) |
| 스택(stack) | O(n) | O(n) | O(1) | O(1) |
| 큐(queue) | O(n) | O(n) | O(1) | O(1) |
| 이중 연결 리스트(doubly linked list) | O(n) | O(n) | O(1) | O(1) |
| 해시 테이블(hash table) | O(1) | O(1) | O(1) | O(1) |
| 이진 탐색 트리(BST) | O(logn) | O(logn) | O(logn) | O(logn) |
| AVL 트리 | O(logn) | O(logn) | O(logn) | O(logn) |
| 레드 블랙 트리 | O(logn) | O(logn) | O(logn) | O(logn) |
자료 구조의 최악 시간 복잡도
| 자료구조 | 접근 | 탐색 | 삽입 | 삭제 |
|---|---|---|---|---|
| 배열(array) | O(1) | O(n) | O(n) | O(n) |
| 스택(stack) | O(n) | O(n) | O(1) | O(1) |
| 큐(queue) | O(n) | O(n) | O(1) | O(1) |
| 이중 연결 리스트(doubly linked list) | O(n) | O(n) | O(1) | O(1) |
| 해시 테이블(hash table) | O(1) | O(1) | O(1) | O(1) |
| 이진 탐색 트리(BST) | O(n) | O(n) | O(n) | O(n) |
| AVL 트리 | O(logn) | O(logn) | O(logn) | O(logn) |
| 레드 블랙 트리 | O(logn) | O(logn) | O(logn) | O(logn) |
제니벨로그