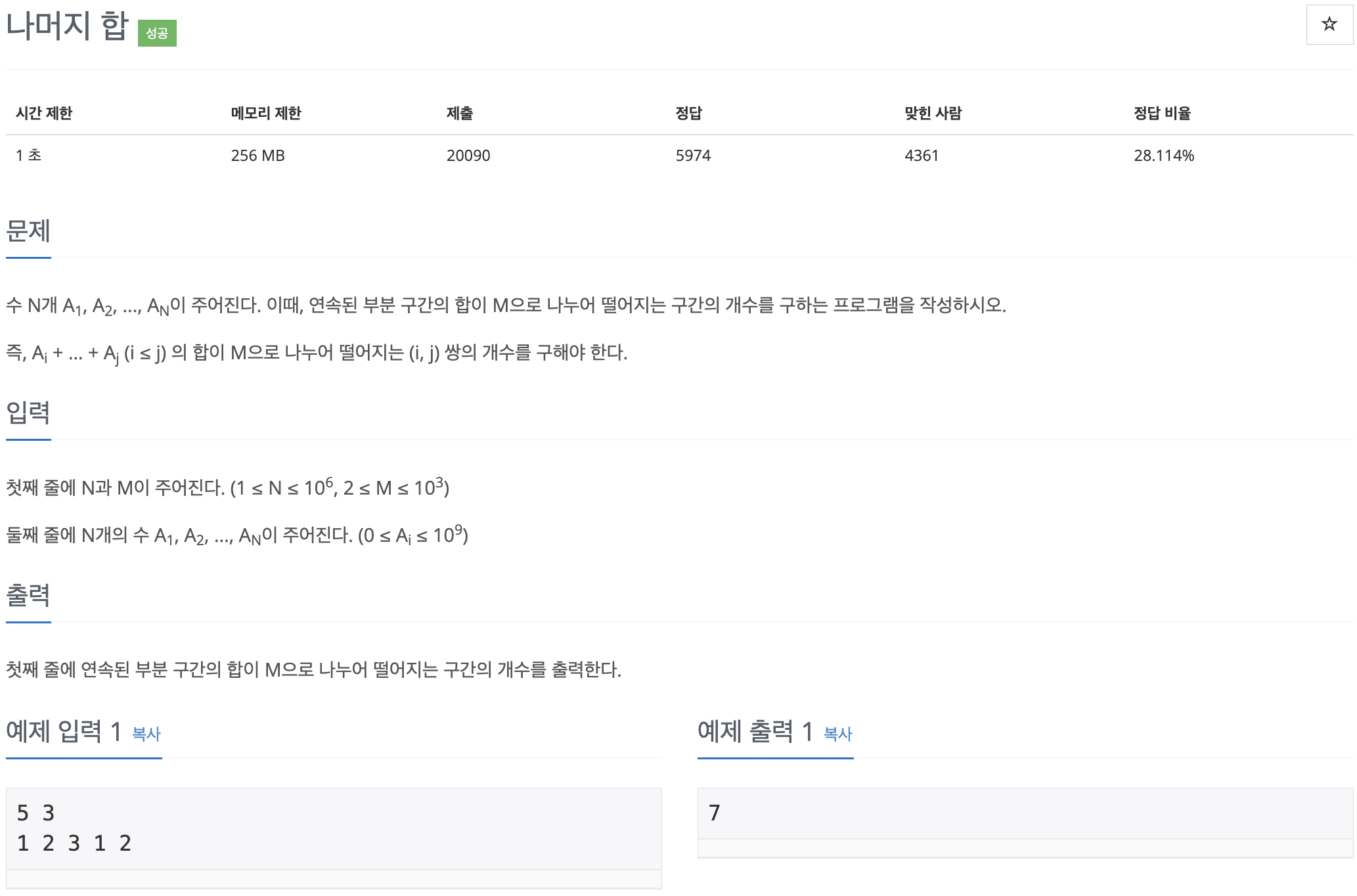
문제
코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.*;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int N = Integer.parseInt(st.nextToken());
int M = Integer.parseInt(st.nextToken());
long[] sumArray = new long[N];
long[] remainderArray = new long[M];
long count = 0;
st = new StringTokenizer(br.readLine());
sumArray[0] = Integer.parseInt(st.nextToken());
for (int i = 1; i < sumArray.length; i++) {
sumArray[i] = sumArray[i - 1] + Integer.parseInt(st.nextToken());
}
for (long value : sumArray) {
int remainder = (int) (value % M);
if (remainder == 0) count++;
remainderArray[remainder]++;
}
for (long value : remainderArray) {
if (value > 1) count += (value * (value - 1)) / 2;
}
System.out.println(count);
}
}리뷰

인생 첫 골드문제이다 😤
이전에 풀었던 구간합 알고리즘을 활용하여 푸는 문제이다.
문제에서 원하는 결과는 무엇을 뜻하는 걸까?
배열의 구간합이 M으로 나누어 떨어지는 i, j쌍의 개수란
1 2 3 1 2 라는 값이 있을 때
어디서부터 어디까지 더하면 3으로 나누어 떨어질까?
1번부터 5번까지라고 가정하면
1번+2번, 1번+2번+3번, 1번+2번+3번+4번+5번,
2번+3번+4번,
3번, 3번+4번+5번,
4번+5번
이렇게 7가지나되는 구간이 나온다.
(골드부터는 문제를 이해하는 것도 일인건가 😞)
여기서 곱셈공식처럼 한 가지 법칙이있다.
각 수의 나머지를 구하고 그 둘을 더해 다시 나머지를 구한 것과
각 수를 더하고 더한 수의 나머지를 구한 값은 같다는 것이다.
식만 봐서는 이해가 안가서 예시를 들어보면
1과 2가 있고 숫자 3으로 이를 나눈다고 생각해보자
1을 3으로 나눈 나머지는 1, 2를 3으로 나눈 나머지는 2이고 이 나머지들의 합은 1 + 2 = 3이다. 이 나머지의 합을 3으로 나눈 나머지는 0이다.
다음 방법인 1과 2를 우선 더하면 3이다. 이를 3으로 나눈 나머지는 0이다.
즉 나머지를 구하고 구하고 더하고 구하는 4번의 계산이 더하고 구하는 2번의 계산으로도 같은 결과를 얻는다.
이러한 특성을 이용하여 푸는게 이번 문제의 핵심이다.
즉 구간합 배열을 주어진 수로 나눈 나머지의 결과값을 저장한 배열을 이용하면 간단하게 문제를 해결할 수 있다.
나누는 수 : 3
1 2 3 1 2 - 입력 배열
1 3 6 7 9 - 구간합 배열
1 0 0 1 0 - 구간합을 주어진 수로 나눈 나머지배열
나머지 배열이 0인 곳은 구간합이 나누어 떨어진다는 것이므로 0의 갯수인 3개가 결과값에 포함된다.
그리고 기존의 구간합 원리를 생각해보면 같은 나머지 값을 가지는 칸의 구간의 나머지는 0이다.
무슨 말이냐면 1이 있는 1번과 4번의 값은 입력 배열에서 1과 1+2+3+1한 값이다 즉 4번에서 1번을 뺀 2 3 1 이 구간의 합을 3으로 나누게되면 0으로 나누어 떨어진다.
같은 나머지 값을 가지고 있다는 것은 두 구간의 사이가 결국 3으로 나누어 떨어지는 수의 차이만큼 벌어져있다는 소리이다.
글로 설명하는데 한계가 있어서 뭔가 확연하게 이해하기 쉬울 수는 없을 것이라 생각되서 이 영상을 추천한다.
나도 이 문제를 이해하는데 도움을 많이 받은 영상이다.
이제 그럼 결과인 7은 어떻게 나오는 것이냐면
나머지 배열의 0의 갯수 3 + 2개의 1에서 한 구간을 뽑는 경우의 수(2C2) + 3개의 0에서 한 구간을 뽑는 경우의 수 (3C2)로 결과값인 7이 도출된다.