[백준] 11660 합 구하기 5 - Java

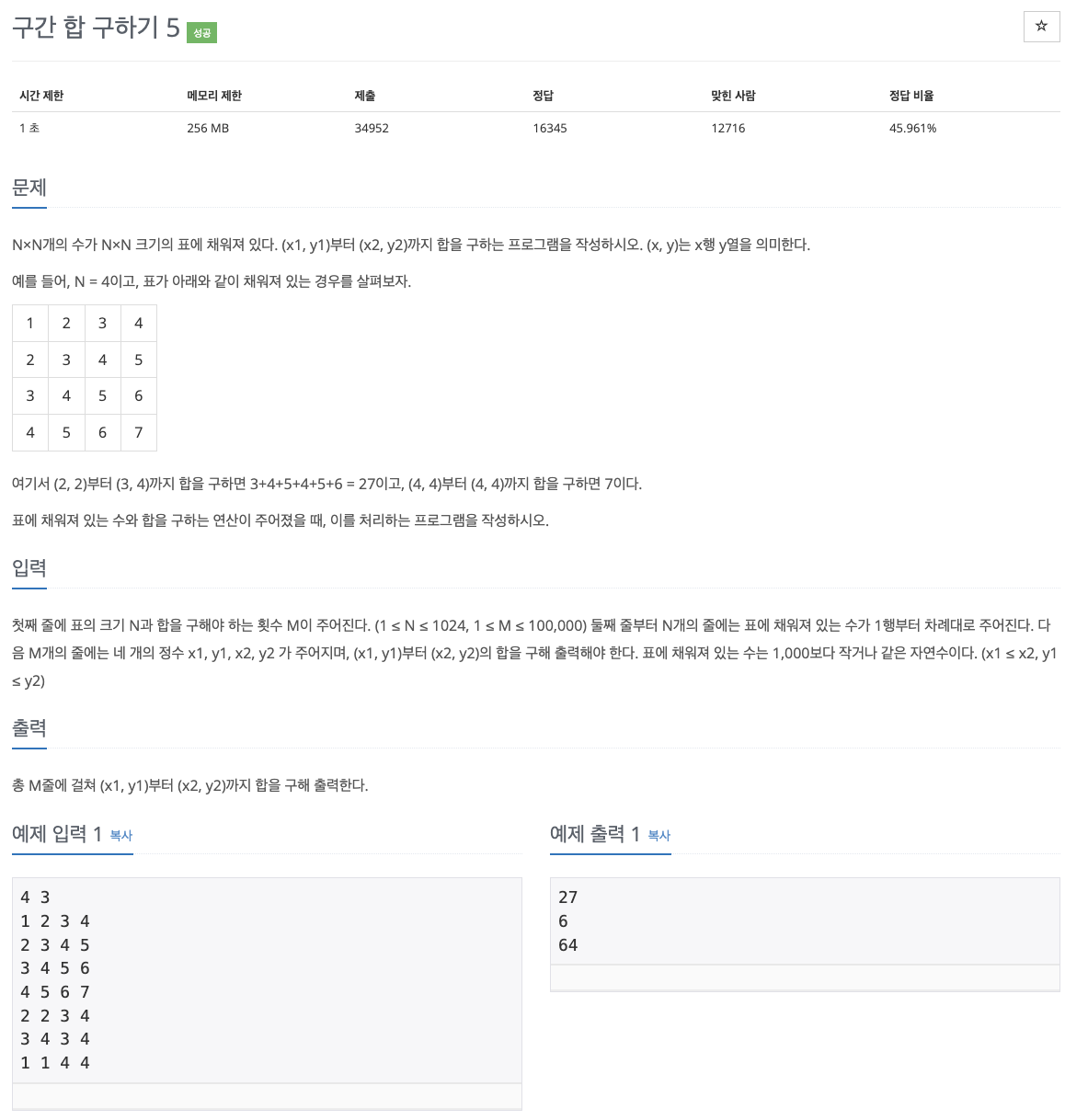
문제

링크

---

코드

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.*;

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());
        int N = Integer.parseInt(st.nextToken());
        int M = Integer.parseInt(st.nextToken());

        int[][] inputArray = new int[N + 1][N + 1];
        for (int i = 1; i < inputArray.length; i++) {
            st = new StringTokenizer(br.readLine());
            for (int j = 1; j < inputArray[i].length; j++) {
                inputArray[i][j] = Integer.parseInt(st.nextToken());
            }
        }

        int[][] sumArray = new int[N + 1][N + 1];
        for (int i = 1; i < sumArray.length; i++) {
            for (int j = 1; j < sumArray[i].length; j++) {
                sumArray[i][j] = sumArray[i][j - 1] + sumArray[i - 1][j] - sumArray[i - 1][j - 1] + inputArray[i][j];
            }
        }

        StringBuilder sb = new StringBuilder();
        for (int i = 0; i < M; i++) {
            st = new StringTokenizer(br.readLine());
            int x1 = Integer.parseInt(st.nextToken());
            int y1 = Integer.parseInt(st.nextToken());
            int x2 = Integer.parseInt(st.nextToken());
            int y2 = Integer.parseInt(st.nextToken());

            sb.append(sumArray[x2][y2] - sumArray[x1 - 1][y2] - sumArray[x2][y1 - 1] + sumArray[x1 -1][y1 - 1])
                    .append("\n");
        }
        br.close();
        System.out.print(sb);
    }
}

---

리뷰

이전에 풀었던 구간합 문제는 1차원배열이고 이번 문제는 2차원배열에서의 구간합 문제이다.

복잡해보이지만 원리는 동일하다.
처음 봤을 때는 이해가 안갔는데 그림으로 이해하는 편이 쉽게 이해할 수 있는 것 같다.

구간합 배열 작성하기

2차원배열의 구간합 배열을 구하기 위해서는

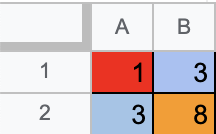
1차원배열에서 이전 인덱스의 구간의 합에 본인 자리에 입력받은 배열의 값을 더해주었듯이 같은 맥락으로 생각하면 된다.

같은 행에서 이전 인덱스의 구간합 값 + 같은 열에서 이전 인덱스의 구간합 값을 더하고
겹치는 부분을 빼주고 본인 자리의 입력받은 배열값을 더해주면 되는 것이다.
sumArray[i][j] = sumArray[i][j - 1] + sumArray[i - 1][j] - sumArray[i - 1][j - 1] + inputArray[i][j];

구간합 배열을 이용한 구간 사이의 합 구하기

이전에 1차원배열에서의 i부터 j구간까지의 합을 구할 때 구간합 배열에서
처음부터 j까지의 구간합 즉 배열[j] 의 값에서 필요없는 처음부터 i - 1구간을 뺐던 것처럼 생각하면 간단하다.

이차원 배열에서는

이 구간의 합을 얻고싶으면

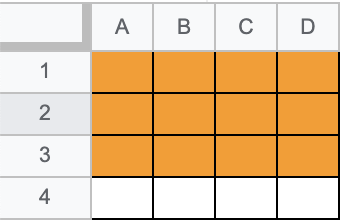
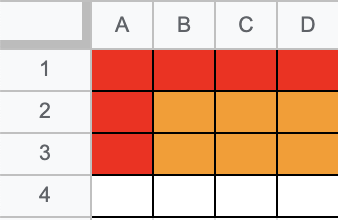
주황색 구간합(3, D) 값에서 빨간색 부분인 구간합(3,A)와 구간합(1,D)를 빼주고 빨간색 부분에서 유일하게 겹치는 구간합(1,A) 부분을 더해주면된다.

이 공식이 코드의
sumArray[x2][y2] - sumArray[x1 - 1][y2] - sumArray[x2][y1 - 1] + sumArray[x1 -1][y1 - 1]
이 부분인 것이다.