[백준] 11659 구간 합 구하기 4 - Java

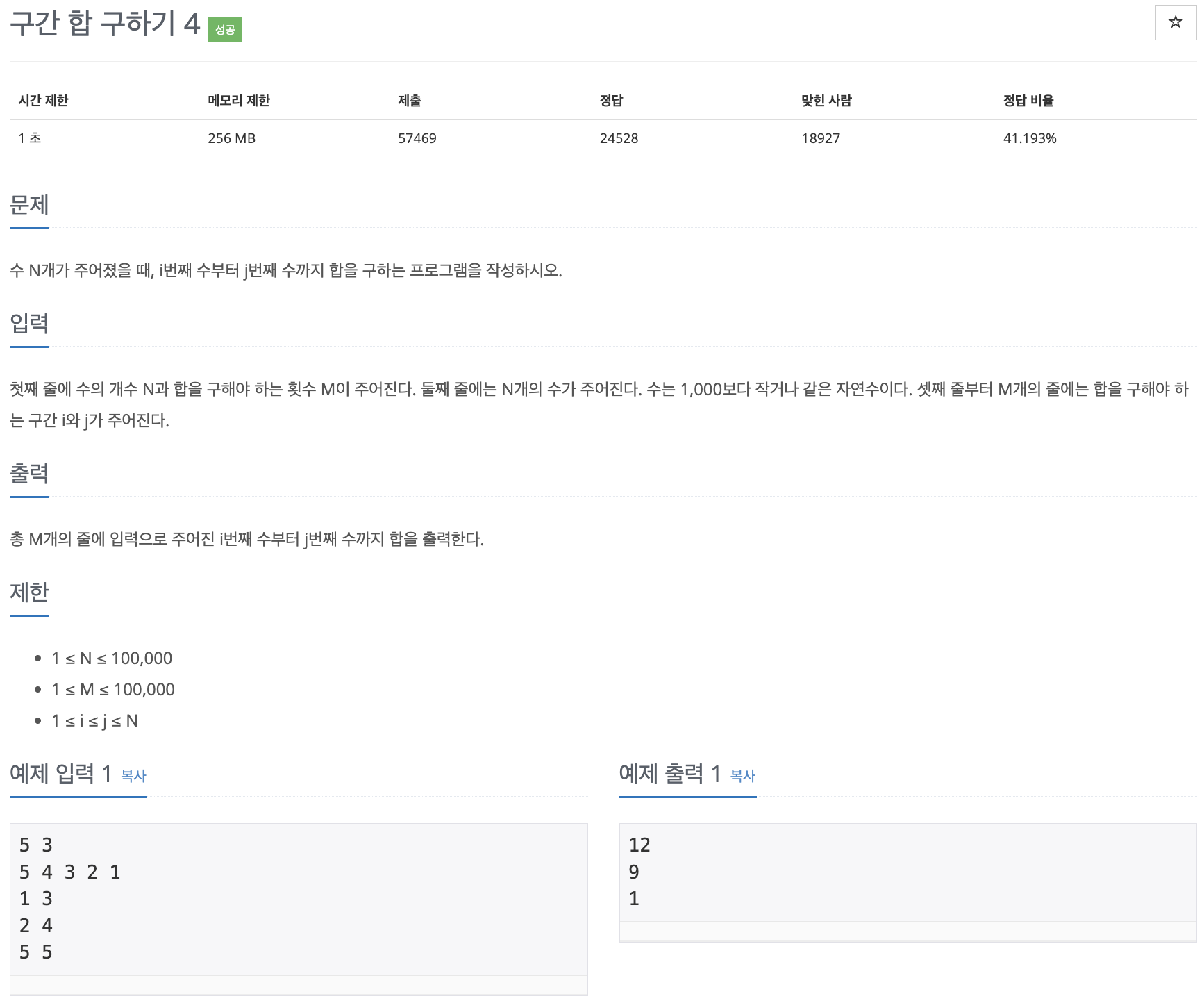
문제

링크

---

코드

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.*;

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());
        int N = Integer.parseInt(st.nextToken());
        int M = Integer.parseInt(st.nextToken());

        int[] sumArray = new int[N + 1];
        st = new StringTokenizer(br.readLine());
        for (int i = 1; i < sumArray.length; i++) {
            sumArray[i] = sumArray[i -1] + Integer.parseInt(st.nextToken());
        }

        StringBuilder sb = new StringBuilder();
        for (int k = 0; k < M; k++) {
            st = new StringTokenizer(br.readLine());
            int i = Integer.parseInt(st.nextToken());
            int j = Integer.parseInt(st.nextToken());
            sb.append(sumArray[j] - sumArray[i - 1]).append("\n");
        }
        br.close();
        System.out.print(sb);
    }
}

---

리뷰

문제를 어느정도 풀고나니 대부분 계산 등을 이용한 구현문제가 대부분이였고 요즘 알고리즘도 하나씩 공부해야 될 것 같아 누적합(구간합) 알고리즘에 대해 공부하며 문제를 풀어보았다.

문제를 얼핏보면 입력받은 수를 배열에 넣어놓고 i부터 j까지 그냥 배열에서 바로 더해서 출력하면 되는게 아닌가 싶지만 알고리즘 문제의 경우 평소에 우리가 빠르게 풀던 반복문을 그냥 돌리는 형태로는 시간 복잡도에 의해 실패가 되는 경우가 많다.

최악의 경우 배열이 100,000의 크기를 가지고 100,000개의 질의가 들어오면 100,000 * 100,000 = 100억
100억건의 연산으로 보통 1억당 1초로보니 100초가 걸려 문제의 조건인 1초를 훨씬 뛰어넘는 시간이다.

그런데 입력받은 배열의 구간별로 합을 저장한 배열을 만들게되면 질의 1건당 O(1)의 연산이 필요해 100,000건으로 여유롭게 시간 제한안에 들어가게된다.
(시간 복잡도 개념이 아직 익숙하지 않아 위의 계산들이 틀릴 수 있다.)

결론은 시간초과를 막으려면 구간합 알고리즘을 사용해야한다는 결론이다.

구간합의 값은 구간합 배열의 이전 인덱스의 값 + 입력받은 배열의 현재 인덱스 값이다. (sumArray[i] = sumArray[i - 1] + array[i])
반복문을 통해 입력받는 동시에 바로 구간합 배열을 만들어주고 입력을 통해 들어온 구간범위에 따른 값을 출력해주면된다.

구간합은 i부터 j의 범위공식은 summArray[j] - sumArray[i - 1]이다.

[0][0][X][X][X] 3부터 5의 구간 범위를 구하고 싶으면
[X][X][X][X][X] 1부터 5의 구간합에서
[X][X][O][O][O] 1부터 2의 구간합을 빼주면 구할 수 있는 것이다.
즉 sumArray[5] - sumArray[2]로 위의 공식과 동일하다.