[Data Structure] 트리, 이진 탐색 트리 Tree, BST

🌟 트리 Tree

정의

노드로 이루어진 자료구조

개념

• 하나의 루트 노드를 갖음

• 0개 이상의 자식 노드를 가짐

• 그 자식 노드 또한 자식 노드를 갖고 이를 반복함

• 노드와 노드를 간선으로 연결

용어

루트 노드(root node): 부모가 없는 노드, 트리는 하나의 루트 노드만을 가짐
단말 노드(leaf node): 자식이 없는 노드, ‘말단 노드’ 또는 ‘잎 노드’
간선(edge): 노드를 연결하는 선 (link, branch)
형제(sibling): 같은 부모를 가지는 노드
노드의 크기(size): 자신을 포함한 모든 자손 노드의 개수
노드의 차수(degree): 하위 트리 개수 / 간선 수 (degree) = 각 노드가 지닌 가지의 수
트리의 차수(degree of tree): 트리의 최대 차수
트리의 높이(height): 루트 노드에서 가장 깊숙히 있는 노드의 깊이

---

🌟 이진 트리

정의

각 노드가 최대 두 개의 자식을 갖는 트리

이진 트리 탐색

배열

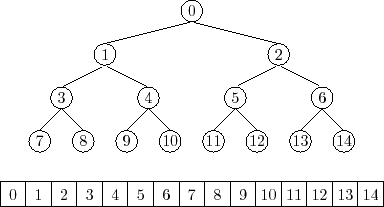
연결 리스트

전위 탐색

현재 노드 -> 왼쪽 간선 -> 오른쪽 간선

배열

void preorder(char *t, int n, int size){	//전위 탐색
	if((n > size> || (t[n] == 0)){
		return;
	}
    print("%c ", t[n]);
    preorder(t, 2*n, size);	// 왼쪽 간선
    preorder(t, 2*n+1, size);	// 오른쪽 간선
}

연결 리스트

preorder(treeNode* root){
	if(root){
    print("%c ", root -> data)
    preorder(root -> left);
    preorder(root -> right);
    }
}

중위 탐색

왼쪽 간선 -> 현재 노드 -> 오른쪽 간선

배열

void inorder(char *t, int n, int size){
	if((n > size) || (t[n] == 0){
    return;
    }
    inorder(t, 2*n, size);	// 왼쪽 간선
    print("%c ", t[n]);
    inorder(t, 2*n+1, size);	// 오른쪽 간선
}

연결 리스트

inorder(treeNode* root){
	if(root){
    inorder(root -> left);
    print("%c ", root -> data);
    inorder(root -> right);
    }
}

후위 탐색

왼쪽 간선 -> 오른쪽 간선 -> 현재 노드

배열

void postorder(char *t, int n, int size){
	if((n > size) || (t[n] == 0)){
		return;
	}
    postorder(t, 2*n, size);
    postorder(t, 2*n+1, size);
    print("%c ", t[n]);
}

연결 리스트

postorder(treeNode* root){
	if(root){
    postorder(root -> left);
    postorder(root -> right);
    }
}

---

🌟 이진 탐색 트리

구성

• 서로 다른 유일한 값

• 왼쪽 서브 트리에 있는 값은 루트의 값보다 작음

• 오른쪽 서브 트리에 있는 값은 루트의 값보다 큼

• 왼쪽 서브 트리, 오른쪽 서브 트리 모두 이진 탐색 트리

이진 탐색

• 루트 노드의 값을 찾고자 하는 값과 비교

• 찾고자 하는 값과 같다면 탐색 완료
  같지 않다면 크기 비교 후 왼쪽 or 오른쪽으로 이동
  

• 값을 찾을 때까지 반복

삽입과 삭제의 원리는 여기서 보는 것이 제일 이해가 잘 된다.

[알고리즘] Binary Search Trees_2편 ( 삽입, 삭제 )
(amuamuamu2.log)

Search

treeNode* searchBST(treeNode* root, char x){
	treeNode *search = root;
    
    if(search == NULL){ 	// 값이 없다면
    	printf("찾는 키가 없습니다");
    	return search;
    }
    else if(x == search -> key){	// 값과 같다면
    return search;
    }
    else if(x < search -> key)	// 값보다 작다면
    	search = searchBST(search -> left, x);
    else if(x > searxh -> key)	// 값보다 크다면
    	search = searchBST(search -> right, x);
}

Insert

treeNode* insertNode(treeNode *p, element x) 
{ 
   treeNode *search = searchBST(p, x);	// 중복 체크
   if (p == NULL){	// root가 없다면
      p = (treeNode*)malloc(sizeof(treeNode));
      p -> key = x;
      p -> left = NULL;
      p -> right = NULL;
      return p;
   }
   
   else if(search != NULL){
      printf("\n이미 같은 키가 있습니다!");
      return ;
   }
   
   else{
      treeNode *newNode = (treeNode *)malloc(sizeof(treeNode));
      newNode -> key = x;
      newNode -> left = NULL;
      newNode -> right = NULL;
      
      treeNode *position = p;
      
      while(1){
         if(x < position -> key){	// 값보다 작고
            if(position -> left == NULL){	// NULL이라면
               position -> left = newNode;
               return ;
            }
            position = position -> left;	// 값이 존재한다면 다시 left
         }
         else{	// 값보다 크고
            if(position -> right == NULL){	// NULL이라면
               position -> right = newNode;	
               return ;
            }
            position = position -> right;	// 값이 존재한다면 right
         }
      }
   }
   
} 

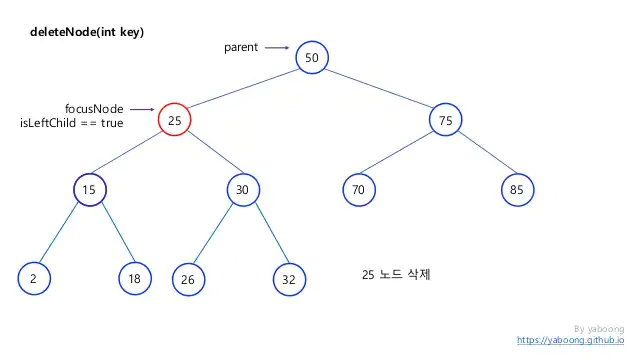
Delete

void deleteNode(treeNode *root, element key ) {
   treeNode *parent, *p, *succ, *succ_parent;
   // 삭제할 노드의 부모 노드, 삭제할 노드, 후보 노드, 후보 노드의 부모 노드
   treeNode *child;
   
   parent = NULL;
   p = root;
   while( (p != NULL) && (p->key != key)){
      parent = p;
      if( key < p -> key ) p = p -> left;
      else p = p -> right;	// 왼쪽 or 오른쪽 결정 
   }
   
   if( p == NULL ){	// 값이 없을 때
      printf("\n 찾는 키가 이진 트리에 없습니다!!");
      return;
   }
   
   else if( (p->left == NULL) && (p->right == NULL) ){	// 단말 노드일 때
      if(parent -> left == p){
         parent -> left = NULL;
         free(p);
      }
      
      else if(parent -> right == p){	// 오른쪽 받으면
         parent -> right = NULL;
         free(p);
      }
   }
   
   else if( (p->left == NULL ) || (p->right == NULL) ){	
   // 왼쪽이나 오른쪽의 값이 없을 때
      if(parent -> left == p){	// 완쪽인지 확인
         if(p -> left != NULL){
            parent -> left = p -> left;
            free(p);
         }
         else if(p -> right != NULL){
            parent -> left = p -> right;
            free(p);
         }
      }
      
      else if(parent -> right == p){	//
         if(p -> left != NULL){
            parent -> right = p -> left;
            free(p);
         }
         else if(p -> right != NULL){
            parent -> right = p -> right;
            free(p);
         }
      }
   }
   else{
      succ_parent = p;
      succ = p -> left;
      
      while(succ -> right != NULL){
         succ_parent = succ;
         succ = succ -> right;
      }   
      
      p -> key = succ -> key;
      if(succ_parent -> left == succ){
         succ_parent -> left = succ -> left;
      
      }
      else if(succ_parent -> right == succ){
         succ_parent -> right = succ -> left;
      }
      p = succ;
   }
   free(p);
   return;
      
}

---

당신의 시간이 헛되지 않는 글이 되겠습니다.
I'll write something that won't waste your time.