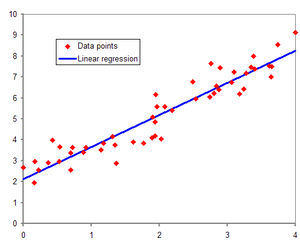
선형 회귀 Linear Regresstion 완벽 정복
경사 하강법
경사하강법(Gradient Descent)은 기계학습에서 가장 일반적으로 사용되는 최적화 알고리즘 중 하나
손실 함수(Loss Function)를 최소화하는 모델의 파라미터를 찾기 위해 사용
경사하강법은 기본적으로 현재 파라미터 값에서 손실 함수의 기울기(Gradient)를 계산하여
파라미터 값을 계산하는 방식으로 동작
이때 기울기의 반대 방향으로 일정 크기의 스텝(Step)을 내딛어 파라미터 값을 업데이트
아래 이미지는 경사하강법이 어떻게 동작하는지를 시각화한 것
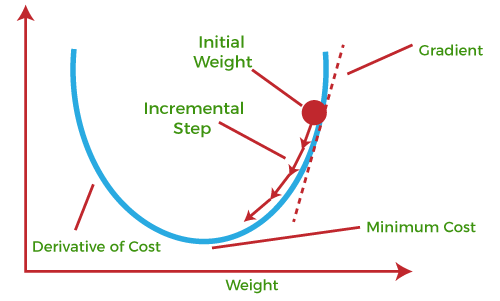
위 그림에서는 파란색 선이 손실 함수의 그래프를 나타내고 있음
경사하강법은 기울기(Gradient)를 계산하여 파라미터 값을 업데이트하는 방식으로 동작
기울기가 양수이면 파라미터 값을 감소시켜 손실 함수의 값을 축소
그 반대의 경우, 즉 기울기가 음수일 때는 파라미터 값을 증가시켜 손실 함수의 값을 축소
위 그림에서 빨간색 화살표가 나타내는 것은 파라미터 값을 업데이트하는 방향
파라미터 값이 업데이트될 때마다, 새로운 파라미터 값에 대응하는 손실 함수의 값이 축소
이와 같은 방식으로 경사하강법은 주어진 손실 함수를 최소화하는 모델의 파라미터를 찾음
선형회귀(Linear Regression)
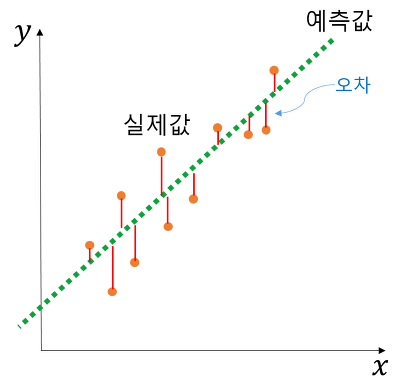
주어진 데이터 셋에서 독립 변수(X)와 종속 변수(Y) 간의 선형 관계를 모델링하는 기법입니다.
선형회귀 모델은 주어진 데이터를 가장 잘 설명할 수 있는 최적의 직선을 찾는 과정에서 오차를 최소화하는 방식으로 동작합니다. 일반적으로, 최소 제곱법(Least Squares Method)이라는 방법을 사용하여 오차를 계산합니다. 이 방법은 오차의 합을 최소화하는 방식으로 선형 회귀 모델을 학습합니다.
선형회귀 모델은 각 독립 변수에 대한 계수와 상수항으로 이루어진 모델입니다. 일반적으로, 선형 회귀 모델은 Y = b0 + b1X1 + b2X2 + ... + bnXn과 같은 형태로 표현됩니다. 여기서 b0는 상수항을 나타내며, b1, b2, ..., bn은 각 독립 변수(X1, X2, ..., Xn)에 대한 계수를 나타냅니다.
선형회귀 모델은 회귀 분석(Regression Analysis)의 한 종류로, 예측 모델링, 통계적 분석, 경제학, 자연 과학, 의학 등 다양한 분야에서 사용됩니다.
로지스틱 회귀(Logistic regression)
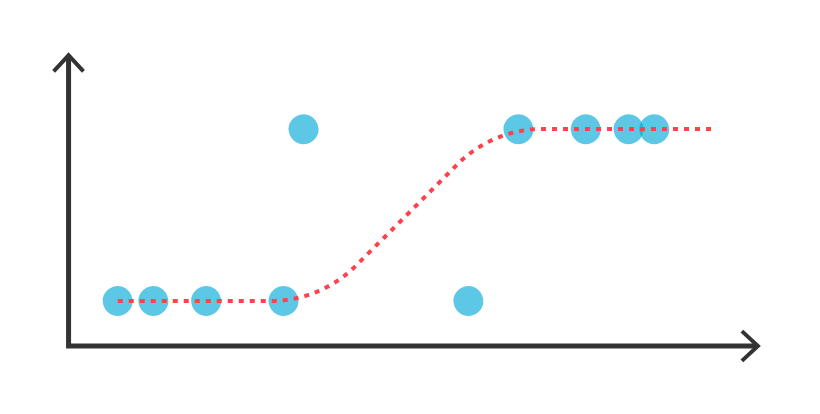
로지스틱 회귀는 이진 분류 문제에서 매우 흔히 사용되는 알고리즘입니다. 로지스틱 회귀는 선형 회귀 모델을 확장한 모델로, 입력값을 선형적으로 결합한 후, 시그모이드 함수를 사용해 0과 1 사이의 값으로 변환하여 이진 분류를 수행합니다.
TensorFlow를 사용한 로지스틱 회귀 모델 구현 코드는 다음과 같습니다.
import tensorflow as tf
import numpy as np
# 학습 데이터
train_x = np.array([[1., 2.], [2., 3.], [3., 1.], [4., 3.], [5., 3.], [6., 2.]])
train_y = np.array([[0.], [0.], [0.], [1.], [1.], [1.]])
# 입력값과 출력값을 담을 placeholder
x = tf.placeholder(tf.float32, [None, 2])
y = tf.placeholder(tf.float32, [None, 1])
# 가중치와 편향 변수 선언
W = tf.Variable(tf.zeros([2, 1]))
b = tf.Variable(tf.zeros([1]))
# 시그모이드 함수 정의
y_pred = tf.sigmoid(tf.matmul(x, W) + b)
# 비용 함수 정의
cost = tf.reduce_mean(-y * tf.log(y_pred) - (1 - y) * tf.log(1 - y_pred))
# 경사 하강법 최적화 함수 정의
learning_rate = 0.01
optimizer = tf.train.GradientDescentOptimizer(learning_rate).minimize(cost)
# 세션 시작
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
# 학습 수행
for i in range(1000):
_, c = sess.run([optimizer, cost], feed_dict={x: train_x, y: train_y})
if i % 100 == 0:
print("Epoch:", '%04d' % (i+1), "cost=", "{:.9f}".format(c))
# 테스트 데이터에 대한 예측 수행
test_x = np.array([[1., 5.], [2., 6.], [3., 3.]])
test_y = sess.run(y_pred, feed_dict={x: test_x})
print("Predictions:", test_y)위 코드에서는 학습 데이터를 train_x와 train_y로 정의하고, 입력값과 출력값을 담을 x와 y placeholder를 정의합니다. 가중치와 편향 변수는 W와 b로 선언하고, 시그모이드 함수는 tf.sigmoid(tf.matmul(x, W) + b)로 정의합니다. 비용 함수는 로지스틱 회귀의 목적 함수인 로그 손실 함수(cost = tf.reduce_mean(-y * tf.log(y_pred) - (1 - y) * tf.log(1 - y_pred)))를 사용합니다. 마지막으로, 경사 하강법 최적화 함수를 정의하고, 학습을 수행합니다.
테스트 데이터에 대한 예측은 test_x를 입력값으로 하여, sess.run(y_pred, feed_dict={x: test_x}) 코드를 실행하면 됩니다.