SW역량테스트 A형 대비 알고리즘 정리

Yumi Kim·2025년 2월 15일

Java 알고리즘

목록 보기

12/18

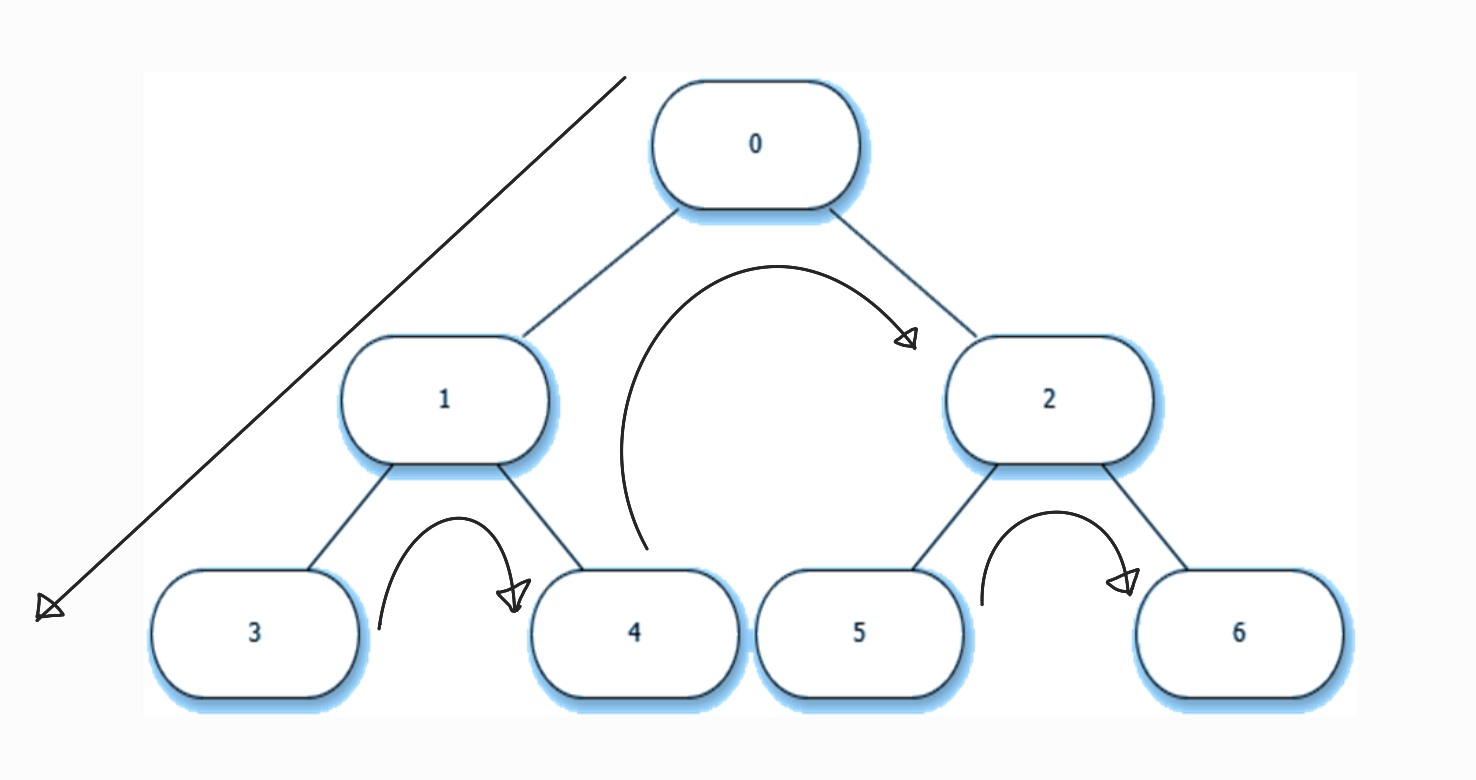
DFS (Depth First Search, 깊이 우선 탐색)

동작 원리 : 스택 (LIFO) or 재귀 함수
활용: 모든 노드를 방문하고 싶을 떄
BFS와 비교 : BFS보다 구현이 간단하지만 검색 속도는 느림
특징 : 미로 탐색 시 더 이상 갈 수 없는 길이면 다시 가장 가까운 갈림길로 돌아와 (백트래킹) 다른 방향으로 다시 탐색을 진행한다.

[수행과정]
1. 탐색 시작 노드를 스택에 삽입 + 방문처리
2. if (스택의 최상단 노드에 방문하지 않은 인접한 노드가 하나라도 있으면), 그 노드를 스택에 삽입 + 방문처리 
 else, 스택에서 최상단 노드를 꺼낸다. 
3. 2번을 반복

public static boolean[] visited = new boolean[그래프 크기];
public static ArrayList<ArrayList<Integer>> graph = new ArrayList<ArrayList<Integer>>();
    
    // dfs
    public static void dfs(int x) {
        // 현재 노드를 방문 처리
        visited[x] = true;
        
        // 현재 노드와 인접한 다른 노드를 재귀적으로 방문
        for (int i = 0; i < graph.get(x).size(); i++) {
            int y = graph.get(x).get(i);
            if (!visited[y]) dfs(y);
        }
    }
    
    // main
    public static void main(String[] args) {
        // 그래프 초기화
        for (int i = 0; i < 9; i++) {
            graph.add(new ArrayList<Integer>());
        }

        // 노드 1에 연결된 노드 정보 저장 
        graph.get(1).add(2);
        graph.get(1).add(3);
        graph.get(1).add(8);
        ... 
        ...
        dfs(1);
     }

BFS (Breadth First Search, 넓이 우선 탐색)

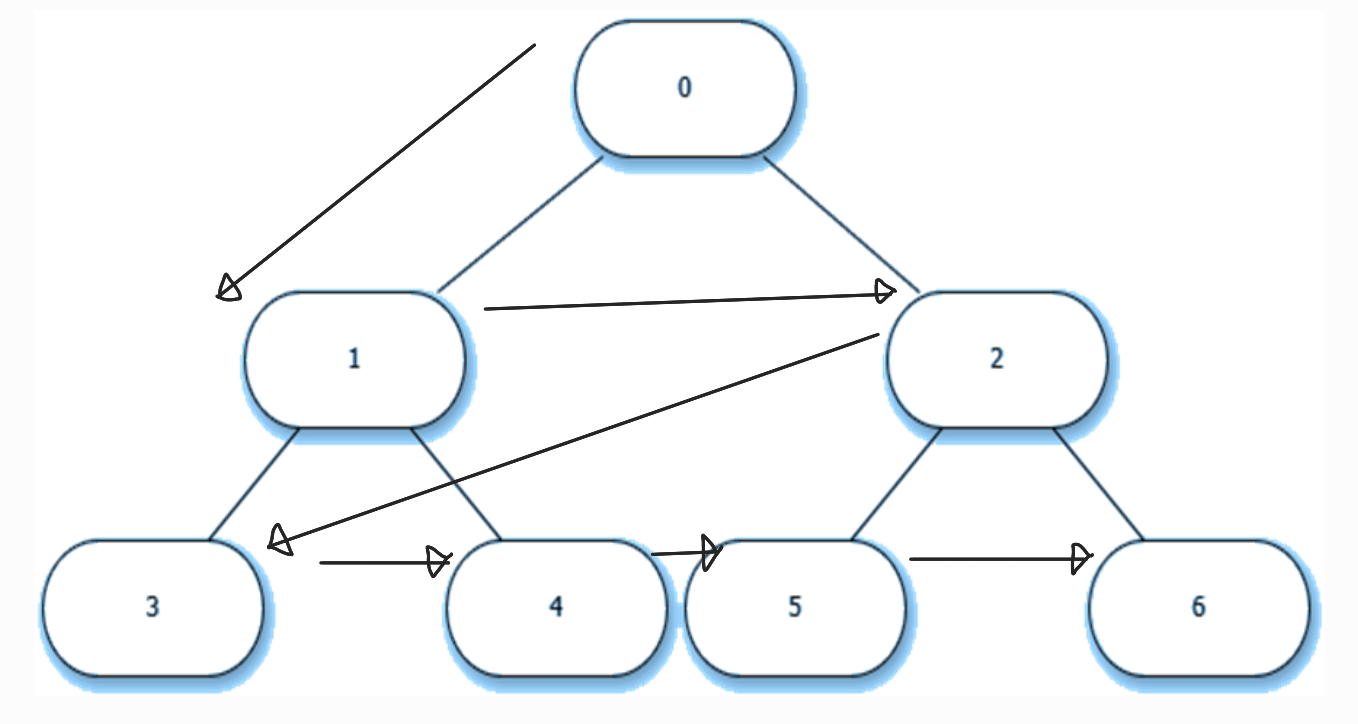
동작 원리 : 큐 (FIFO)
활용 : 두 노드 사이의 최단 경로를 찾을 때
특징 : 가까운 노드부터 우선적으로 탐색한다.

[수행과정]
1. 탐색 시작 노드를 큐에 삽입 + 방문처리
2. 큐에서 노드를 꺼낸 다음, 해당 노드와 인접한 노드 중에서 방문하지 않은 노드를 모두 큐에 삽입 + 방문처리 
 else, 스택에서 최상단 노드를 꺼낸다. 
3. 2번을 반복

public static boolean[] visited = new boolean[그래프 크기];
public static ArrayList<ArrayList<Integer>> graph = new ArrayList<ArrayList<Integer>>();
    
    // bfs
    public static void bfs(int start) {
        Queue<Integer> q = new LinkedList<>();
        q.offer(start);
        
        // 현재 노드를 방문 처리
        visited[start] = true;
        
        // 큐가 빌 때까지 반복
        while(!q.isEmpty()) {
            // 큐에서 하나의 원소를 선택
            int x = q.poll();
            // 해당 원소와 인접한, 아직 방문하지 않은 원소들을 큐에 삽입
            for(int i = 0; i < graph.get(x).size(); i++) {
                int y = graph.get(x).get(i);
                if(!visited[y]) {
                    q.offer(y);
                    visited[y] = true;
                }
            }
        }
    }

DP (Dynamic Programming, 동적 계획법)

: 큰 문제를 작은 문제로 나누어서 푸는 알고리즘 기법.

작은 문제의 답을 별도의 메모리 영역에 저장하고, 추후 재사용 (=Memoization)
작동 원리 : 배열 or 해시 테이블 사용하여 구현
활용 :
1. 최적 부분 구조(Optimal Substructure) :
  큰 문제를 작은 문제로 나누고, 작은 문제의 답을 모아서 큰 문제를 해결
2. 중복되는 부분 문제(Overlapping Subproblem) :
  동일한 작은 문제를 반복적으로 해결
장점 : 단순 재귀 함수보다 높은 효율을 갖는다.

구현 방법 :

Top-Down (재귀) : 큰 문제를 작은 문제로 나눔 -> 작은 문제를 해결

스택 오버플로우 발생 가능성 있음..
분할정복(Divide and Conquer)과 유사한 방식. BUT, 중복되는 작은 문제들을 한번만 푼다는 점에서 차이가 있음.

int dp[] = new int[100];

public int fibonacci(int n) {
    if (n <= 1) return n;

    if (dp[n] != 0) { // dp 배열을 Memoization용으로 사용 
        return dp[n];
    }

    dp[n] = fibonacci(n - 1) + fibonacci(n - 2); // 재귀
    return dp[n];
    }
}

Bottom-Up (반복문) : 크기가 작은 문제부터 씀 -> 문제의 크기를 조금씩 크게 만들면서 해결 -> 작은 문제를 해결하면서 큰 문제를 해결

초기값 설정 필요, 작은 문제들의 결과값을 임시저장할 공간 필요..

int dp[100];
public int fibonacci(int n) {
    dp[0] = 0;
    dp[1] = 1;
    for (int i = 2; i <= n; i++) { // Memoization
        dp[i] = dp[i - 1] + dp[i - 2];
    }
    return dp[n];
}

Backtracking (백트래킹)

: 가능한 모든 경우의 수를 탐색하여 정답을 찾아내는 기법 (DFS의 한 형태)
-> Brute-Force 기법과 달리, 탐색하던 경로에 해가 절대로 없는 상황일 때 탐색을 중지하고 그 이전 경로로 돌아가 다른 경우를 탐색한다. (⨫ 가지치기)
-> 즉, 모든 가능한 경우의 수에서 특정한 조건을 만족하는 경우만 살펴본다..!

작동 원리 : 재귀
활용 :
- 완전탐색을 통해 최적비용/최적경로 탐색
- 순열/조합 생성
- 각 조건에서 선택할 수 있는 경우의 수가 정해져 있는 경우

[코드 구조]
public static void backtrack(상태) : // 1. 문제= 트리구조 & 각 노드=문제의 상태
     if 특정한 조건을 만족하면 : // [탈출 조건]
          해답을 저장 혹은 출력함
          return;
          
     for 가능한 모든 경우의 수 in 현재 상태 : // [경로 탐색]
         if 선택지가 유망하지 않으면, // 2. 가지치기 (값의 유망성을 판단) 
               continue
               
         선택지를 적용 // 값 변경
         backtrack(새로운 상태) // 3. 재귀
         선택지 되돌리기 // 퇴각 검색을 위해 값 원복

Yumi Kim