📖 Pattern Matching

📌 고지식한 패턴 검색 알고리즘 (브루트 포스)

✅ 고지식한 알고리즘 (Brute Force)

• 본 문자열을 처음부터 끝까지 차례대로 순회하면서 패턴 내의 문자들을 일일이 비교하는 방식으로 동작

• 시간 복잡도 : O(N * M)

• N : 문자열 길이, M : 패턴 길이

// p[] : 찾을 패턴 - iss
// t[] : 전체 텍스트 - This iss a book
// M : 찾을 패턴의 길이
// N : 전체 텍스트의 길이
// i : t의 인덱스
// j : p의 인덱스

BruteForce(char[] p, char[] t) {
	i <- 0 j <- 0
    
    while(j<M && i<N) {
    	if(t[i] != p[j]) {
        	i <- i-j;
            j <- -1;
        }
        
        i <- i+1, i <- j+1
    }
    
    if(j == M)
    	return i-M;
    else
    	return -1;
}

✅ 고지식한 패턴 검색 알고리즘의 시간 복잡도

• 최악의 경우 텍스트의 모든 위치에서 패턴을 비교해야 하므로 O(M * N)

• 어떻게 하면 줄일 수 있을까?

📌 KMP 알고리즘

✅ KMP Algorithm

• Knuth, Morris, Pratt의 앞 글자

• 불일치가 발생한 텍스트 문자열의 앞부분에 어떤 문자가 있는지를 미리 알고 있다는 것을 활용

  • 불일치가 발생한 앞 부분에 대하여 다시 비교하지 않고 매칭 수행

• 시간 복잡도 O(N+M)

✅ 접두사 / 접미사

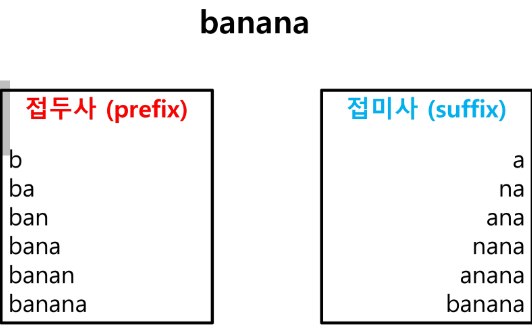
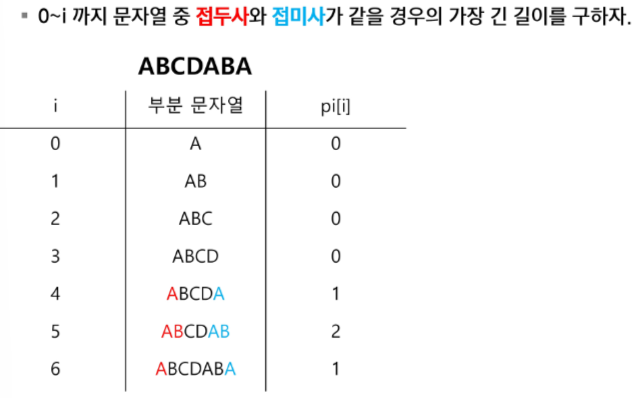
✅ KMP 알고리즘 pi 배열 pseudo code

• pi 배열은 단순하게 구하면 O(m^3)

• 패턴이 크다면 시간이 오래 걸리므로 O(m)의 시간 복잡도로 pi 배열을 구할 수 있다.

static int[] getPi(String pattern) {
	int[] pi = new int[pattern.length()]; // jump 위치 저장
    char[] pt = pattern.toCharArray(); // 문자 배열
    
    int j = 0;
    
    for(int i=1; i<pattern.length(); i++) {
    	while(j>0 && pt[i] != pt[j])   // 최대한 점프
        	j = pi[j-1];
        
        if(p[i] == p[j])
        	pi[i] = ++j;
    }
    
    return pi;
}

✅ KMP 알고리즘 pseudo code

static void KMP(String text, String pattern) {
	int[] pi = getPi(pattern);
    char[] org = text.toCharArray();
    char[] pt = pattern.toCharArray();
    
    int j=0;
    
    for(int i=0; i<text.length(); i++) {
    	while(j>0 && org[i] != pt[j])
        	j = pi[j-1];
         
        if(org[i] == pt[j]) {
        	if(j == pattern.length()-1)
            	j = table[j];
            else
            	j++;
        }
    }
}

📌 카프-라빈 알고리즘

✅ Rabin-Karp

• 문자열 검색을 위해 해시 값 함수 이용

• 패턴의 해시 값과 본문 안에 있는 하위 문자열의 해시 값 만을 비교

• 최악의 시간 복잡도는 O(M * N)이지만, 평균적으로는 선형에 가까운 빠른 속도를 가짐.

✅ 동작 과정

1. 패턴의 해시 값을 계산

2. text에서 패턴의 길이 만큼 잘라서 해시 값 계산

3. 해시 값을 비교하여 패턴의 유무 판단
   3-1> 다음 글자부터는 주어진 해시 값에서 2(해시값 - 첫글자 2^(패턴길이-1) + 다음글자)
   3-2> 패턴의 해시값과 text의 해시 값이 같다면 정확히 일치하는지 두 문자열 비교

4. text 길이 - pattern 길이 만큼 반복하고 종료

✅ Rabin-Karp pseudo code

Rabin_Karp(String text, String pattern) {
	tHash <- Hashing(text[0:패턴길이])
    pHash <- Hashing(pattern)
    
    if(tHash == pHash)
    	check();
        
    for(int i=1; i<text길이-pattern길이+1; i++) {
    	tHash = 2*(tHash-text[i-1]*2^(패턴길이-1)) + text[i]
        
        if(tHash == pHash)
        	check();
            
        // 경우에 따라 Hash 값을 mod 연산하기도 함.
    }
}

Hashing(String str) {
	result = 0;
    
    for(int i=0; i<str.length(); i++) {
    	result *= 2
        result += str.charAt(i)
    }
    
    return result
}

📌 보이어-무어 알고리즘

✅ Boyer-Moore

• 오른쪽에서 왼쪽으로 비교

• 대부분의 상용 소프트웨어에서 채택

• 패턴에 오른쪽 끝에 있는 문자가 불일치 하고, 이 문자가 패턴 내에 존재하지 않으면 이동 거리가 패턴 길이 만큼 씩이나 된다.

✅ 동작 과정

1. 점프 테이블 생성

2. 패턴의 오른쪽 끝부터 비교
   2-1> 글자가 같을 때 왼쪽으로 이동하면서 비교
   2-2> 글자가 다르면서 패턴 내에 글자가 있을 때는 그만큼 점프
   2-3> 글자가 다르면서 패턴 내의 글자가 없을 때는 패턴 길이 만큼 점프

3. 문자열의 끝까지 가면서 비교

✅ Boyer-Moore pseudo code

Boyer-Moore(String text, String pattern) {
	skip_table 생성
    
    j <- 패턴길이-1
    
    for i to text길이 - 패턴길이
    	flag = true
        
        for j to 0
        	if (text[i+j] != pattern[j])
            	flag = false
                
                if(text[i+j] in skip_table)
                	해당 칸 만큼 점프
                else
                	패턴 길이만큼 점프
                    
        if(flag)
        	"해당 패턴 발견!!"
            return true;
            
   return false;
}