📖 Dynamic Programming
📌 피보나치 수열
✅ 피보나치 수를 구하는 재귀함수
fibo(n)
IF n < 2 : RETURN n
ELSE : RETURN fibo(n-1) + fibo(n-2)-
얼마나 중복되었을까?
-
중복을 어떻게 피할 수 있을까?
📌 Memoization
✅ 메모이제이션
-
컴퓨터 프로그램을 실행할 때, 이전에 계산한 값을 메모리에 저장해서 매번 다시 계산하지 않도록 하여 전체적인 실행속도를 빠르게 하는 기술
-
동적 계획법의 핵심이 되는 기술
✅ 메모이제이션 - 피보나치 수
// memo를 위한 배열을 할당하고, 모두 0으로 초기화
// memo[0]을 0으로 memo[1]는 1로 초기화
fibo(n)
IF n>2 AND memo[n] = 0
memo[n] <- fibo(n-1) + fibo(n-2)
RETURN memo[n]✅ 메모이제이션의 구조
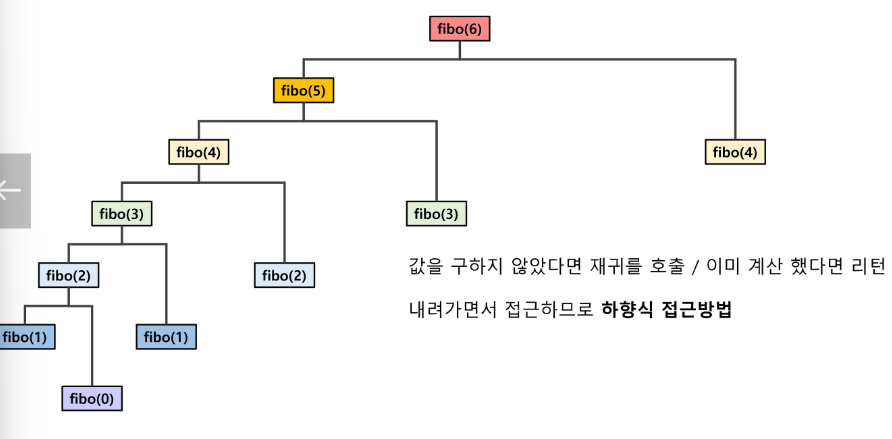
-
값을 구하지 않았다면 재귀 호출/ 이미 계산 했다면 리턴
-
내려가면서 접근하므로 하향식 접근방법
-
추가적인 메모리 공간 필요
-
재귀 함수 호출로 인한 시스템 호출 스택 사용
- -> 실행 속도 저하 또는 Overflow 발생 가능성 있음.
📌 동적 계획 알고리즘
✅ 동적 계획 알고리즘
-
동적 계획 (Dynamic Programming) 알고리즘은 그리디 알고리즘과 같이 최적화 문제를 해결하는 알고리즘
-
최적화 문제 : 최적(최대값이나 최소값) 값을 구하는 문제
- 해당 문제에 여러 해 존재 할 수 있다.
- 특정 최적해를 구하는 것이 아니라, 어떤 최적해를 구하는 것
-
동적 계획 알고리즘은 먼저 작은 부분 문제들의 해들을 구하고, 이들을 이용하여 보다 큰 크기의 부분 문제들을 해결하여, 최종적으로 원래 주어진 문제를 해결하는 알고리즘 설계 기법
✅ 동적 계획법 적용 요건
-
중복 부분문제 구조 (Overlapping subproblems)
-
최적 부분문제 구조 (Optimal substructure)
✅ 중복 부분문제 구조 (Overlapping subproblems)
- DP는 큰 문제를 이루는 작은 문제들을 먼저 해결하고, 작은 문제들의 최적 해(Optimal Solution)을 이용하여 순환적으로 큰 문제를 해결한다.
- 순환적인 관계 (recurrence relation)를 명시적으로 표현하기 위해 동적 계획법에서는 일반적으로 수학적 도구인 점화식을 사용
- DP는 문제의 순환적인 성질 때문에 이전에 계산되어졌던 작은 문제의 해가 다른 어딘가에서 필요하게 되는데, 이를 위해 DP에서는 이미 해결된 작은 문제들의 해들을 어떤 저장 공간(Table)에 저장하게 된다.
- 이렇게 저장된 해들이 다시 필요할 때마다 해를 얻기 위해 다시 문제를 재계산하지 않는다.
- table의 참조를 통해서 중복된 계산을 피한다.
✅ 최적 부분문제 구조 (Optimal substructure)
-
동적 계획법이 최적화에 대한 어느 문제에나 적용되는 것은 아니다.
-
주어진 문제가 최적화의 원칙 (Principle of Optimality)을 만족해야만 동적 계획법을 효율적으로 적용
-
최적화의 원칙이란 어떤 문제에 대한 해가 최적일 때, 그 해를 구성하는 작은 문제들의 해 역시 최적이어야 한다는 것
-
동적 계획법의 방법 자체가 큰 문제의 최적 해를 작은 문제의 최적해들을 이용하여 구하기 때문에 만약 큰 문제의 최적해가 작은 문제들의 최적해들로 구성되지 않는다면 이 문제는 동적 계획법 적용 불가능
-
최적의 원칙이 적용되지 않는 예시 : 최장경로(Longest Path)
✅ 분할 정복과 동적 계획법 비교
- 분할 정복
- 연관 없는 부분 문제로 분할
- 부분문제를 재귀적으로 해결
- 부분문제의 해를 결합
- ex> 병합정렬 / 퀵정렬
- DP
- 부분 문제들이 연관이 없으면 적용 불가능 (즉, 부분 문제들은 더 작은 부분 문제들을 공유)
- 모든 부분 문제를 한번만 계산하고, 결과를 저장하고 재사용(분할 정복은 같은 부분문제가 나타날 경우 다시 계산)
-
DP에는 부분 문제들 사이 의존적 관계 존재
- 이러한 관계는 문제에 따라 다르고 대부분 뚜렷이 보이지 않아 함축적인 순서(Implicit order)라고 한다.
-
분할 정복은 하향식 방법
-
DP는 상향식 방법
✅ 3단계 DP 적용 접근 방법
- 최적해 구조의 특성을 파악하라
- 문제를 부분 문제로 나눈다.
- 최적해의 값을 재귀적으로 정의하라
- 부분 문제의 최적해 값에 기반하여 문제의 최적해 값을 정의
- 상향식 방법으로 최적해의 값을 계산하라
- 가장 작은 부분 문제부터 해를 구한 뒤 테이블에 저장한다.
- 테이블에 저장되어 있는 부분 문제의 해를 이용하여 점차적으로 상위 부분 문제의 최적해를 구한다. (상향식 방법)
✅ 피보나치 수 DP 적용
- 피보나치 수는 부분 문제의 답으로부터 본 문제의 답을 얻을 수 있으므로, 최적 부분구조로 이루어져 있다.
-
문제를 부분 문제로 분할
-
점화식으로 정의
-
가장 작은 부분 문제부터 해를 구한다.
- 그 결과는 테이블에 저장하고, 테이블에 저장된 부분 문제의 해를 이용하여 상위 문제의 해를 구한다.
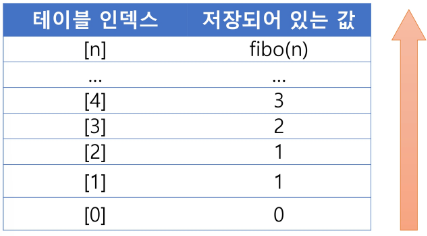
fibo_dp(n)
f[0] <- 0
f[1] <- 1
FOR i in 2 -> n
f[i] <- f[i-1] + f[i-2]
RETURN f[n]-
작은 문제부터 큰 문제까지 올라가면서 해결
-
상향식 접근 방법
✅ 피보나치 수 DP 적용 - 알고리즘 분석
- DP 알고리즘이 수행속도가 더 빠르다.
- 재귀 알고리즘과 달리 중복 계산이 없다.
- 반복문을사용하기에 함수 호출이 발생하지 않는다.
- fibo_dp[0]부터 fibo_dp[n]까지 한번씩만 계산한다.

