📖 Start

📌 자료구조 복습

✅ 자료구조

• 배열 (1차원, 다차원)

• 문자열

• 스택

• 큐

• 연결리스트

• 트리

📌 복잡도 분석

✅ 알고리즘의 효율

• 공간적 효율성과 시간적 효율성
  • 공간적 효율성은 연산량 대비 얼마나 적은 메모리 공간을 요구하는 가
  • 시간적 효율성은 연산량 대비 얼마나 적은 시간을 요구하는 가
  • 효율성을 뒤집어 표현하면 복잡도(Complexity)가 된다.
  • 복잡도가 높을수록 효율성은 저하된다.
• 시간적 복잡도 분석

  • 하드웨어 환경에 따라 처리 시간이 달라진다.

  • 소프트웨어 환경에 따라 처리시간이 달라진다.

    • 프로그램 언어 종류, 운영체제 종류, 컴파일러 종류

  • 이러한 환경적 차이로 인해 정확한 분석이 어렵다.

✅ 복잡도의 점근적 표기

• 시간 (또는 공간)복잡도는 입력 크기에 대한 함수로 표기하는데, 이 함수는 주로 여러 개의 항을 가지는 다항식이다.

• 이를 단순한 함수로 표현하기 위해 점근적 표기(Asymptotic Notation)를 사용한다.

• 입력 크기 n이 무한대로 커질 때으 ㅣ복잡도를 간단히 표현하기 위해 사용하는 표기법

  • O(Big-Oh) 표기
  • Big-Omega 표기
  • Big-Theta 표기

✅ O(Big-Oh) 표기

• O-표기는 복잡도의 점근적 상한을 나타낸다.

• ex> f(n) = 2n^2 - 7n + 4 => f(n)의 O 표기 : O(n^2)

✅ 자주 사용하는 O-표기

• O(1) : 상수 시간 (Constant time)

• O(log n) : 로그(대수) 시간 (Logarithmic time)

• O(n) : 선형 시간(Linear time)

• O(nlogn) : 로그 선형 시간 (Log-linear time)

• O(n^2) : 제곱 시간 (Quadratic time)

• O(n^3) : 세제곱 시간 (Cubit time)

• O(2^n) : 지수 시간 (Exponential time)

✅ 왜 효율적인 알고리즘이 필요한가

• 값 비싼 H/W의 기술 개발보다 효율적인 알고리즘 개발이 훨씬 더 경제적이다.

📌 진수

✅ 진법

• 수를 셀 때, 자릿수가 올라가는 단위를 기준으로 하는 셈법의 총칭

• 일반적으로 10진법

• 시계는 12진법 / 60진법

• 컴퓨터는 2진법

✅ 10진수 -> 타 진수로 변환

• 원하는 타진법의 수로 나눈 뒤 나머지를 거꾸로 읽는다.

• ex> (149)10 = (10010101)2 = (225)8 = (95)16

✅ 컴퓨터에서의 음의 정수 표현 방법

• 부호 비트 (최상위 비트 : 양수 -> 0, 음수 -> 1)

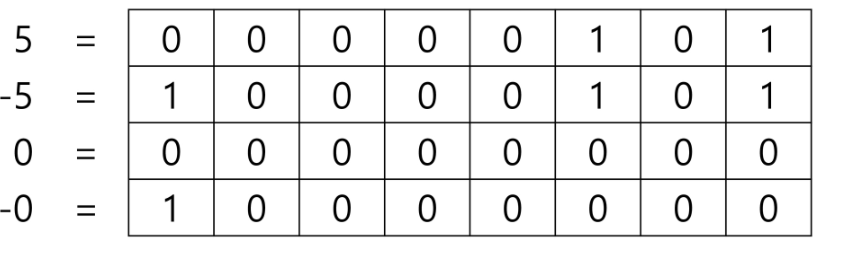
• 근데 위 사진에 의하면 0의 결과가 두개네?

• 1의 보수 : 부호와 절대값으로 표현된 값을 부호 비트를 제외한 나머지 비트들을 0은 1로, 1으 0으로 변환한다.

• 2의 보수 : 1의 보수 방법으로 표현된 값의 최하위 비트에 1을 더한다.

• 그래서 컴터는 2의 보수 사용. 왜일까? 1의보수 왜 안쓸까?

📌 실수

✅ 2진 실수를 10진수로 변환하는 방법

✅ 실수의 표현

• 컴퓨터는 실수를 표현하기 위해 고정 소수점(Fixed Point), 부동 소수점(Floating Point) 표기법을 사용한다.

• 고정 소수점 방식

• 부동 소수점 표기 방법은 소수점의 위치를 고정시켜 표현하는 방식이다.
  • 소수점의 위치를 왼쪽의 가장 유효한 숫자 다음으로 고정시키고 밑수의 지수 승을 표현

위 사진의 0010011 : 가수부, 3 : 지수부

✅ 실수를 저장하기 위한 형식

• 단정도 실수 (32bit) - float
• 배정도 실수 (64bit) - double

• 가수부(mantissa) : 실수의 유효 자릿수들을 부호화된 고정 소수점으로 표현한 것

• 지수부(exponent) : 실제 소수점의 위치를 지수 승으로 표현한 것

📌 비트연산자

✅ 비트연산자