📖 Tree 2

📌 수식 트리

✅ 수식 트리

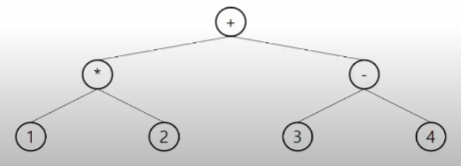
• 수식을 표현하는 이진 트리

• 수식 이진 트리(Expression Binary Tree)라고 부르기도 함

• 연산자는 루트 노드이거나 가지 노드(internal node)

• 피연산자는 모두 잎 노드(leaf node / external node)

• 연산은 아래에서 위로

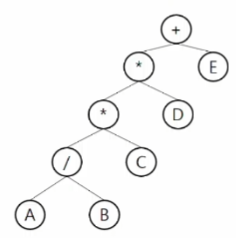
✅ 수식 트리의 순회

• 중위 순회 : A / B C D + E

• 후위 순회 : A B / C D E +

• 전위 순회 : + * * / A B C D E

📌 힙

✅ 힙 (Heap)

• 완전 이진 트리(사실상 배열이랑 같음 얘는)에 있는 노드 중 키 값이 가장 큰 노드나 키 값이 가장 작은 노드를 찾기 위해 만든 자료구조

• 힙에서 Root : 최대값 혹은 최소값

• 최대 힙 (max heap)

  • 키 값이 가장 큰 노드를 찾기 위한 완전 이진 트리
  • 부모 노드의 키 값 >= 자식 노드의 키 값
  • 루트 노드 : 키 값이 가장 큰 노드 (최대값)

• 최소 힙 (min heap)

  • 키 값이 가장 작은 노드를 찾기 위한 완전 이진 트리
  • 부모 노드의 키 값 <= 자식 노드의 키 값
  • 루트 노드 : 키 값이 가장 작은 노드 (최소값)

✅ 힙을 찾는 법

• 최대 힙 찾기

1. 완전 이진 트리인가?

2. 부모 >= 자식 (자식은 최대 2개) - leaf node는 비교할 필요 없음. 자식이 없잖아
   ex> 노드가 총 9개일 때 4개만 조사
   ex> 노드가 총 10개일 때 5개만 조사
   => 총 노드 개수 / 2 만큼만 조사하면 됨. (leaf node는 조사 필요 x)

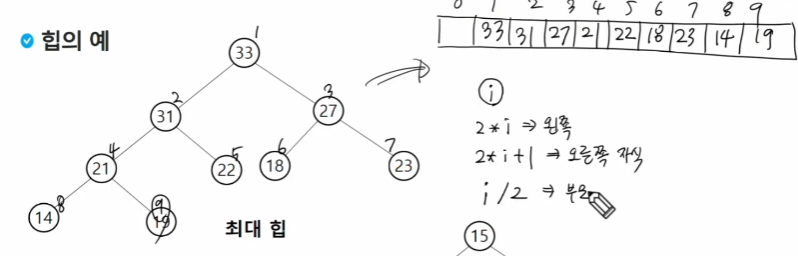
리프노드는 배열 뒤쪽에 다 있다

✅ 힙 삽입

• 시간 복잡도 : O(logN)

1. 17 삽입 - 삽입해도 교환할 필요 없다. (최대 힙 만족)

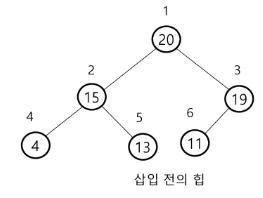
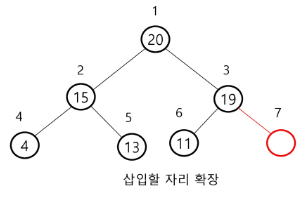
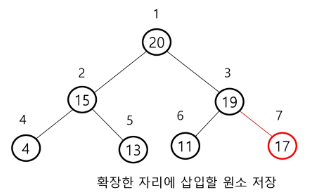
2. 23 삽입 - 교환 두번 (노드 7개 => 교환 2회, 만약 노드 15개 => 교환 3회 ==> logN)

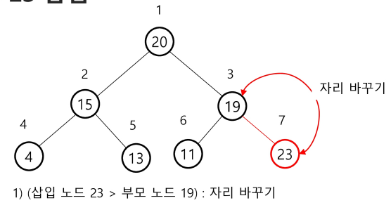
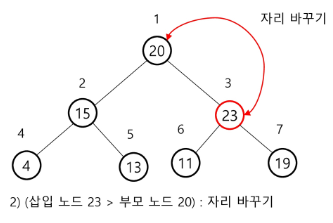
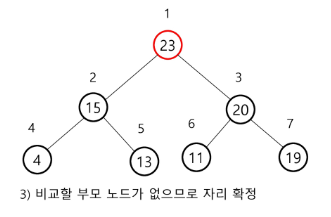
• 삽입한 곳에서 2로 나눈 위치(부모노드)와 비교해서 교환. 루트까지 비교 할때까지 반복.

✅ 힙 삭제

• 힙에서는 루트 노드의 원소만을 삭제할 수 있다. => 정렬하기 편할거같은데,,?
  • Priority Queue : 힙으로 만들어짐.
    
  • 루트 노드의 원소를 삭제하여 반환
  • 힙의 종류에 따라 최대 또는 최소 구할 수 있음

✅ 최대 힙에서의 삭제 예시

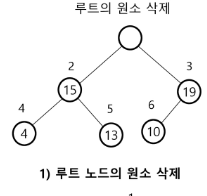
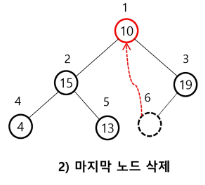
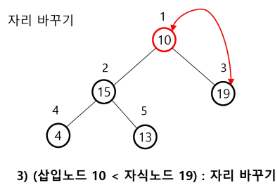
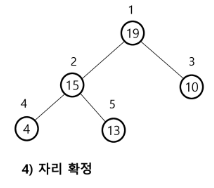
✅ 힙의 활용 1 - 우선 순위 큐 (Priority Queue)

• 우선순위 큐를 구현하는 가장 효율적인 방법 : 힙 활용

  • 노드 추가/삭제 : O(logN)
  • 최대/최소 : O(1)
  • 완전 정렬보다 관리 비용이 적다.

• 부모/자식 노드를 O(1) 연산으로 손쉽게 구할 수 있다.

• n 위치의 노드의 자식은 2*n, 2*n +1

• 완전 이진 트리의 특성에 의해 추가/삭제를 자료의 시작과 끝 인덱스를 활용하여 손쉽게 할 수 있다.

✅ 힙의 활용 2 - 힙 정렬

• 시간 복잡도 : O(Nlog N)
  • N개의 삽입연산 / N개의 삭제 연산
  • 한번 삽입/삭제 연산은 O(logN)
• 정렬 과정

1. 하나의 값을 힙에 삽입(반복)
2. 힙에서 순차적으로 값을 하나씩 제거