📖 그래프 최소 비용 1
📌 서로소 집합 (Disjoint Sets)
✅ 서로소 집합 (상호배타 집합)
- 서로소 또는 상호배타 집합들은 서로 중복 포함된 원소가 없는 집합들
- 교집합이 없다
- 집합에 속한 하나의 특정 멤버를 통해 각 집합들을 구분한다.
- 이를 대표자(representative) 라고 한다.
-
상호배타 집합을 표현하는 방법
- 연결 리스트
- 트리
-
상호배타 집합 연산
- Make-Set(x) : 집합 생성 - x라고 하는 원소를 대표자로 하는 x 집합 생성
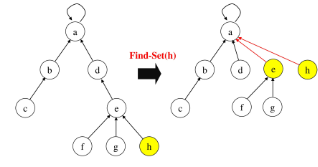
- Find-Set(x) : x 집합의 대표자 가져와
- Union(x, y) : 두 집합을 하나의 그룹으로 만든다.
✅ 상호 배타 집합 표현 - 연결리스트
-
같은 집합의 원소들은 하나의 연결리스트로 관리한다.
-
연결리스트의 맨 앞의 원소를 집합의 대표 원소로 삼는다.
-
각 원소는 집합의 대표원소를 가리키는 링크를 갖는다.
✅ 상호 배타 집합 표현 - 트리
-
하나의 집합(a disjoint set)을 하나의 트리로 표현한다.
-
자식 노드가 부모 노드를 가리키며 루트 노드가 대표자가 된다.
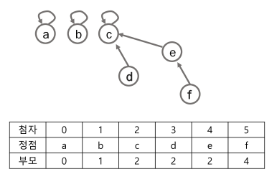
✅ 상호배타 집합 연산
- Make-Set(x) : 유일한 멤버 x를 포함하는 새로운 집합을 생성하는 연산
Make-Set(x)
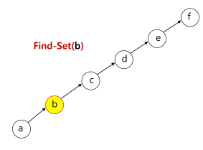
p[x] <- x- Find-Set(x) : x를 포함하는 집합을 찾는 연산
Find-Set(x)
IF x == p[x] : RETURN x
ELSE : RETURN Find-Set(p[x])- Union(x, y) : x와 y를 포함하는 두 집합을 통합하는 연산
- x라는 집합에 y가 들어가는 것임
Union(x, y)
p[Find-Set(y)] <- Find-Set(x)✅ 문제점
-
균형있게 만들었다면 좋았을텐데..
-
편향 트리가 될 수 있을 것 같은데?
✅ 연산 효율을 높이는 방법
-
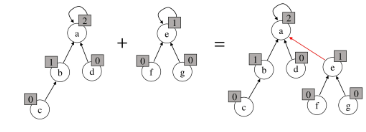
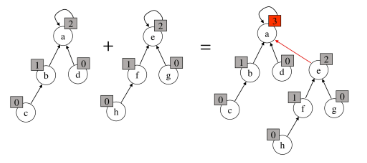
Rank를 이용한 Union
- 각 노드는 자신을 루트로 하는 subtree의 높이를 랭크(rank)라는 이름으로 저장한다.
- 두 집합을 합칠 때 rank가 낮은 집합을 rank가 높은 집합에 붙인다.
-
Path compression
- Find-Set을 행하는 과정에서 만나는 모든 노드들이 직접 root를 가리키도록 포인터를 바꿔준다.
✅ Make-Set 연산
- 유일한 멤버 x를 포함하는 새로운 집합을 생성하는 연산
// p[x] : 노드 x의 부모 저장
// rank[x] : 루트 노드가 x인 트리의 랭크 값 저장
Make-Set(x)
p[x] <- x
rank[x] <- 0✅ Find-Set 연산
- x를 포함하는 집합을 찾는 오퍼레이션
Find-Set(x)
IF x != p[x] : // x가 루트가 아닌 경우
p[x] <- Find-Set(p[x])
RETURN p[x]- Find-Set 연산은 특정 노드에서 루트까지의 경로를 찾아 가면서 노드의 부모 정보를 갱신한다.
✅ Union 연산
- Union(x, y) : x와 y를 포함하는 두 집합을 통합하는 오퍼레이션
Union(x, y)
Link(Find_Set(x), Find_Set(y))Link(x, y)
IF rank[x] > rank[y] : // rank는 트리의 높이
p[y] <- x
ELSE
p[x] <- y
IF rank[x] == rank[y] :
rank[y]++📌 최소 비용 신장 트리
✅ 최소 신장 트리 (MST, Minimum Spanning Tree)
-
신장 트리 : 그래프의 모든 정점과 간선의 부분집합으로 구성되는 트리
-
최소 신장 트리 : 신장 트리 중, 사용된 간선들의 가중치의 합이 최소인 트리
-
특징
- 무방향 가중치 그래프
- 그래프의 가중치의 합이 최소
- N개의 정점을 가지는 그래프에 대해 반드시 (N-1)개의 간선을 사용해야 한다.
- 사이클 포함 X
-
사용 이유
- 도로망, 통신망, 유통망 등 여러 분야에서 비용을 최소로 해야 이익을 볼 수 있다.
-
대표적인 방법
- Kruskal
- Prim
📌 크루스칼 알고리즘
✅ KRUSKAL 알고리즘
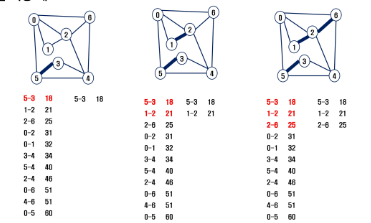
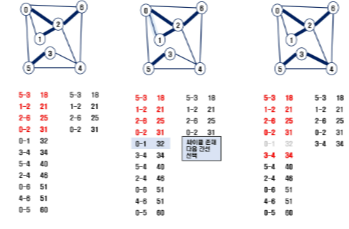
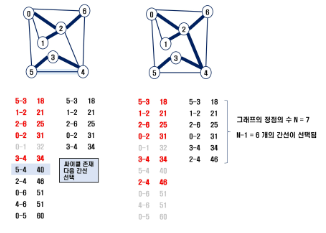
- 간선을 하나씩 선택해서 MST를 찾는 알고리즘
1) 최초, 모든 간선을 가중치에 따라 오름차순 정렬
2) 가중치가 가장 낮은 간선부터 선택하면서 트리 증가
- 사이클이 존재하면 다음으로 가중치가 낮은 간선 선택
3) n-1개의 간선이 선택될 때 까지 2를 반복
✅ 알고리즘
MST-KRUSKAL(G, w)
A <- 0 // 0 : 공잡헙
FOR vertex v in G.V // G.V : 그래프의 정점 집합
Make_Set(v) // G.E : 그래프의 간선 집합
G.E에 포함된 간선들을 가중치 w에 의해 정렬
FOR 가중치가 가장 낮은 간선 (u, v) G.E 선택 (n-1개)
IF Find_Set(u) != Find_Set(v)
A <- A U {(u, v)};
Union(u, v);
RETURN A
