📖 그래프 최소 비용 2
📌 프림 알고리즘
✅ 프림 알고리즘 (Prim)
- 하나의 정점에서 연결된 간선들 중 하나씩 선택하면서 MST를 만들어 가는 방식
1) 임의 정점을 하나 선택해서 시작
2) 선택한 정점과 인접하는 정점들 중 최소 비용의 간선이 존재하는 정점을 선택
3) 모든 정점이 선택될 때 까지 1, 2 과정 반복
- 서로소인 2개의 집합 (2 disjoint-sets) 정보를 유지
- 트리 정점들 (tree vertices) - MST를 만들기 위해 선택된 정점들
- 비트리 정점들 (nontree vertices) - 선택 되지 않은 정점들
✅ 프림 알고리즘 적용 예시
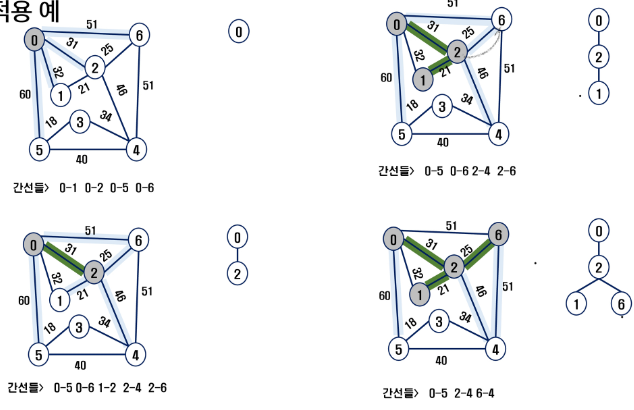
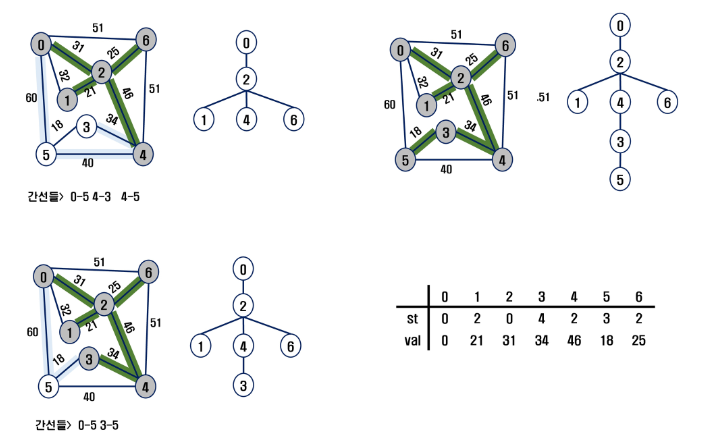
✅ 프림 알고리즘 pseudo code
MST_PRIM(G, r) // G : 그래프, r : 시작 정점
FOR u in G.V
u.key <- INF // u.key : u에 연결된 간선 중 최소 가중치
u.pi <- NULL // u.pi : 트리에서 u의 부모
r.key <- 0
Q <- G.V // 우선순위 Q에 모든 정점 삽입
WHILE Q != 0 // 빈 Q가 아닐동안 반복
u <- Extract_MIN(Q) // key 값이 가장 작은 정점 가져오기
FOR v in G.Adj[u] // u의 인접 정점들
IF v ( Q AND w(u, v) < v.key // Q에 있는 v의 key값 갱신
v.pi <- u
v.key <- w(u, v)📌 다익스트라 알고리즘
✅ 최단 경로
-
최단 경로 정의 : 간선의 가중치가 있는 그래프에서 두 정점 사이의 경로들 중에 간선의 가중치의 합이 최소인 경로
-
하나의 시작 정점에서 끝 정점까지의 최단 경로
- 다익스트라(Dijkstra) 알고리즘 (음의 가중치 허용 X)
- 벨만-포드(Bellman-Ford) 알고리즘 (음의 가중치 허용 O)
-
모든 정점들에 대한 최단 경로
- 플로이드-워샬(Floyd-Warshall) 알고리즘
✅ 다익스트라 알고리즘
-
시작 정점에서 거리가 최소인 정점을 선택해 나가면서 최단 경로를 구하는 방식
-
탐욕 기법을 사용한 알고리즘으로 MST의 프림 알고리즘과 유사
-
시작 정점(s)에서 끝 정점(t)까지의 최단 경로에 정점 x가 존재
-
이 때, 최단 경로는 s에서 x까지의 최단 경로와 x에서 t까지의 최단 경로로 구성된다.
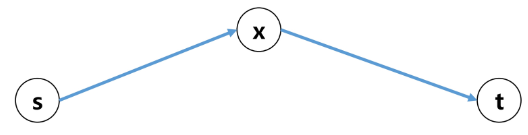
- s->t까지의 최단 경로 = s->x까지 최단 경로 + x->t까지 최단 경로
✅ 다익스트라 알고리즘 동작 과정
-
시작 정점을 입력 받는다.
-
거리를 저장할 D 배열을 INF로 초기화한 후, 시작점에서 갈 수 있는 곳의 값은 바꿔 놓는다.
-
아직 방문하지 않은 점들이 가지고 있는 거리 값과 현재 정점에서 방문하지 않은 정점까지의 가중치의 합이 작다면 변경하여 적는다.
-
모든 정점을 방문할 때까지 반복
✅ 다익스트라 알고리즘 pseudo code
// G : 그래프, r : 시작 정점, S : 선택된 정점 집합
// D : 출발점에서 각 정점까지 최단 경로 가중치 합 저장
// P : 최단 경로 트리 저장, ADJ(u) 정점 u의 인접 정점 집합
Dijkstra(G, r)
S <- ?
FOR ALL v ( V
D[v] <- INF
P[v] <- NULL
D[r] <- 0
WHILE S != V
D[u]가 최소의 정점 u ( V - S를 선택
S <- S U {u}
FOR ALL v ( ADJ(u)
IF v ( V - S AND D[v] > D[u] + weight(u, v)
D[v] = D[u] + weight(u, v)
P[v] = u✅ 음의 가중치
- 음의 가중치가 있다면 Dijkstra 알고리즘은 사용하면 안된다.

