백준 1912번

연속합

문제

n개의 정수로 이루어진 임의의 수열이 주어진다. 우리는 이 중 연속된 몇 개의 수를 선택해서 구할 수 있는 합 중 가장 큰 합을 구하려고 한다. 단, 수는 한 개 이상 선택해야 한다.

예를 들어서 10, -4, 3, 1, 5, 6, -35, 12, 21, -1 이라는 수열이 주어졌다고 하자. 여기서 정답은 12+21인 33이 정답이 된다.

입력

첫째 줄에 정수 n(1 ≤ n ≤ 100,000)이 주어지고 둘째 줄에는 n개의 정수로 이루어진 수열이 주어진다. 수는 -1,000보다 크거나 같고, 1,000보다 작거나 같은 정수이다.

출력

첫째 줄에 답을 출력한다.

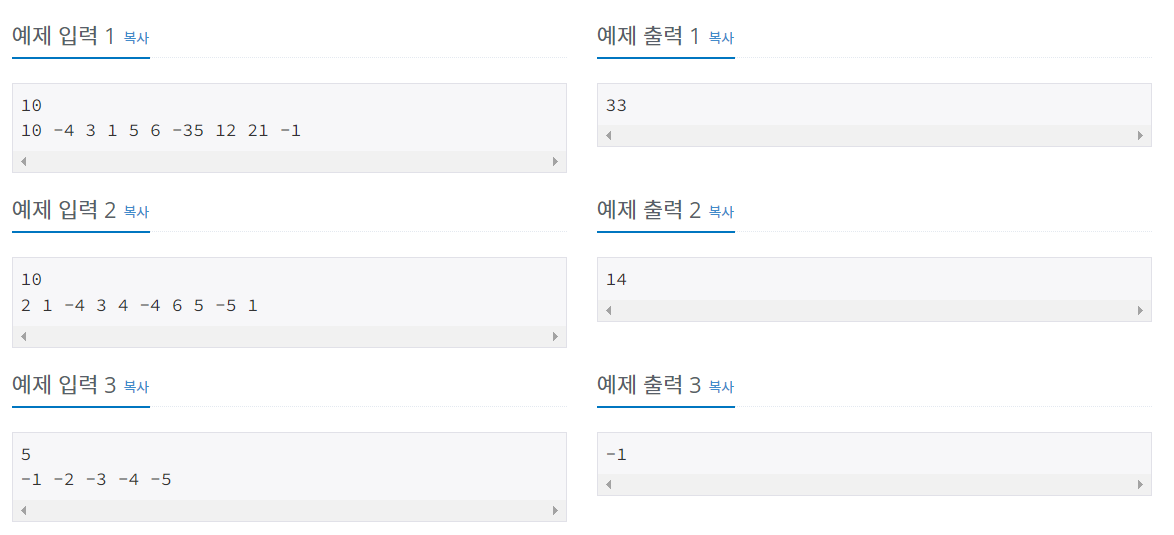
예제

알고리즘 분류

• DP

코드

import java.util.*;
import java.io.*;

public class Main {
	static Integer dp[];
	static int arr[];
	static int max;
	
	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		
		int N = Integer.parseInt(br.readLine());
		
		arr = new int[N];
		dp = new Integer[N];
		
		StringTokenizer st = new StringTokenizer(br.readLine(), " ");
		
		for(int i=0; i<N; i++)
			arr[i] = Integer.parseInt(st.nextToken());
		
		dp[0] = arr[0];
		max = arr[0];
		
		DP(N-1);
		
		System.out.println(max);
	}
	
	static int DP(int N) {
		if(dp[N] == null) {
			dp[N] = Math.max(DP(N-1) + arr[N], arr[N]);
			max = Math.max(dp[N], max);
		}
		
		return dp[N];
	}
}

풀이

Dynamic Programming을 재귀를 활용하는 Top-Down 방식으로 해결한다.
중복을 고려하지 않아도 된다.