백준 1149번

RGB거리

문제

RGB거리에는 집이 N개 있다. 거리는 선분으로 나타낼 수 있고, 1번 집부터 N번 집이 순서대로 있다.

집은 빨강, 초록, 파랑 중 하나의 색으로 칠해야 한다. 각각의 집을 빨강, 초록, 파랑으로 칠하는 비용이 주어졌을 때, 아래 규칙을 만족하면서 모든 집을 칠하는 비용의 최솟값을 구해보자.

• 1번 집의 색은 2번 집의 색과 같지 않아야 한다.
• N번 집의 색은 N-1번 집의 색과 같지 않아야 한다.
• i(2 ≤ i ≤ N-1)번 집의 색은 i-1번, i+1번 집의 색과 같지 않아야 한다.

입력

첫째 줄에 집의 수 N(2 ≤ N ≤ 1,000)이 주어진다. 둘째 줄부터 N개의 줄에는 각 집을 빨강, 초록, 파랑으로 칠하는 비용이 1번 집부터 한 줄에 하나씩 주어진다. 집을 칠하는 비용은 1,000보다 작거나 같은 자연수이다.

출력

첫째 줄에 모든 집을 칠하는 비용의 최솟값을 출력한다.

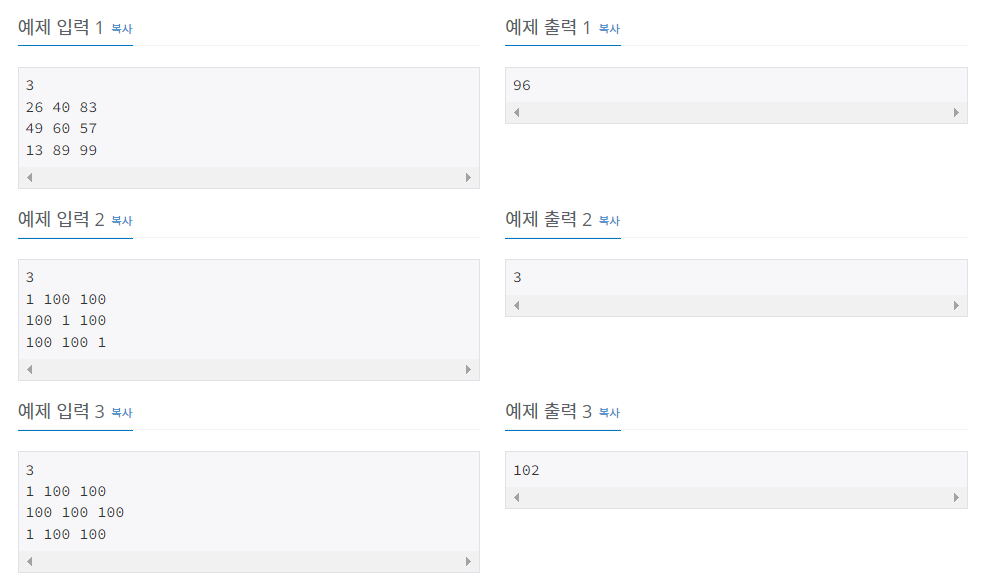
예제

알고리즘 분류

• 다이나믹 프로그래밍

코드

import java.util.*;
import java.io.*;

public class Main {
	static final int Red = 0;
	static final int Green = 1;
	static final int Blue = 2;
	
	static int Price[][];
	static int DP[][];
	
	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		
		int N = Integer.parseInt(br.readLine());
		
		Price = new int[N][3];
		DP = new int[N][3];
		
		StringTokenizer st;
		
		for(int i=0; i<N; i++) {
			st = new StringTokenizer(br.readLine(), " ");
			
			Price[i][Red] = Integer.parseInt(st.nextToken());
			Price[i][Green] = Integer.parseInt(st.nextToken());
			Price[i][Blue] = Integer.parseInt(st.nextToken());
		}
		
		DP[0][Red] = Price[0][Red];
		DP[0][Green] = Price[0][Green];
		DP[0][Blue] = Price[0][Blue];
		
		System.out.println(Math.min(Func(N-1, Red), Math.min(Func(N-1, Green), Func(N-1, Blue))));
	}
	
	public static int Func(int N, int color) {
		if(DP[N][color] == 0) {
			switch(color) {
				case Red:
					DP[N][Red] = Math.min(Func(N-1, Green), Func(N-1, Blue)) + Price[N][Red];
					break;
				case Green:
					DP[N][Green] = Math.min(Func(N-1, Blue), Func(N-1, Red)) + Price[N][Green];
					break;
				case Blue:
					DP[N][Blue] = Math.min(Func(N-1, Red), Func(N-1, Green)) + Price[N][Blue];
					break;
			}
		}
		
		return DP[N][color];
	}
}

풀이

DP 유형 문제는 역시 규칙을 잘 찾아 점화식을 잘 세우는 것이 중요하다.
단순히 매집마다 최솟값을 고르면 모두 합해봤을 때 당연히 틀린다.
Math.min() 함수를 활용하여 점화식을 구성한다.

Red = 0, Green = 1, Blue = 2라고 하면,

Red일 때 Price[N][0] = Math.min(Price[N-1][1], Price[N-1][2]) + Price[N][0]
Green일 때 Price[N][1] = Math.min(Price[N-1][2], Price[N-1][0]) + Price[N][1]
Blue일 때 Price[N][2] = Math.min(Price[N-1][0], Price[N-1][1]) + Price[N][2]
임을 알 수 있다.