백준 1920번

수 찾기

문제

N개의 정수 A[1], A[2], …, A[N]이 주어져 있을 때, 이 안에 X라는 정수가 존재하는지 알아내는 프로그램을 작성하시오.

입력

첫째 줄에 자연수 N(1 ≤ N ≤ 100,000)이 주어진다. 다음 줄에는 N개의 정수 A[1], A[2], …, A[N]이 주어진다. 다음 줄에는 M(1 ≤ M ≤ 100,000)이 주어진다. 다음 줄에는 M개의 수들이 주어지는데, 이 수들이 A안에 존재하는지 알아내면 된다. 모든 정수의 범위는 -231 보다 크거나 같고 231보다 작다.

출력

M개의 줄에 답을 출력한다. 존재하면 1을, 존재하지 않으면 0을 출력한다.

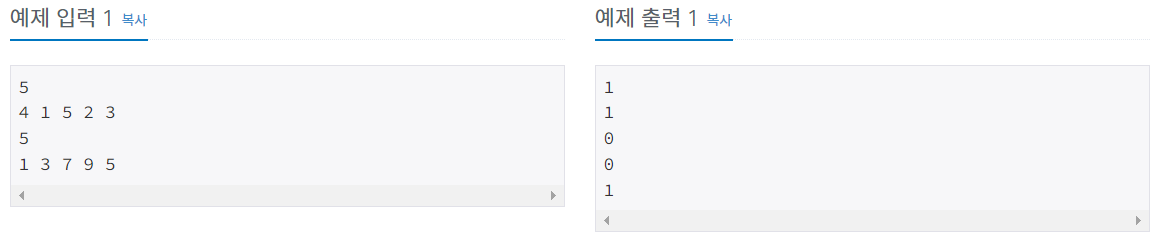
예제

코드

import java.util.*;
import java.io.*;

public class Main {
	public static int arr[];
	
	public static void main(String[] args) throws IOException{
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		
		int N = Integer.parseInt(br.readLine());
		arr = new int[N];
		
		StringTokenizer st = new StringTokenizer(br.readLine(), " ");
		
		for(int i = 0; i < N; i++) {
			arr[i] = Integer.parseInt(st.nextToken());
		}
		
		Arrays.sort(arr);
		
		int M = Integer.parseInt(br.readLine());
		st = new StringTokenizer(br.readLine(), " ");
		StringBuilder sb = new StringBuilder();
	
		for(int i = 0; i < M; i++) {
			if(BinarySearch(Integer.parseInt(st.nextToken())) >= 0) 
				sb.append(1).append('\n');
			else 
				sb.append(0).append('\n');
		}
		System.out.println(sb);
	}

	public static int BinarySearch(int key) {
		int first = 0;					
		int last = arr.length - 1;	
 
		while(first <= last) {
			int center = (first + last) / 2;	
 
			if(key < arr[center]) 
				last = center - 1;
			
			else if(key > arr[center]) 
				first = center + 1;
			
			else 
				return center;
		}
		return -1;
	}
}

풀이

이 문제는 이분 탐색(Binary Search) 알고리즘을 활용하여 문제를 해결한다.
이 문제에서의 포인트는 '수가 존재하는지'만 알아내면 되기 때문에 중복 원소에 대한 고려는 하지 않고 구현한다.
또한 이분 탐색을 하기 위해서는 배열이 반드시 정렬 되어있어야 한다.

이분(진) 탐색의 방법
1. 탐색 범위내의 배열의 중간 인덱스를 구한다.
2. 중간 인덱스의 값과 key값을 비교한다.
3. 값이 중간 값보다 작다면 왼쪽 부분을, 값이 중간 보다 크다면 오른쪽 부분을 탐색하고, 같다면 해당 인덱스를 반환하고 종료한다.

결과

• 찾으려는 값을 찾았을 경우
• 찾으려는 값이 없을 경우

탐색 범위의 왼쪽 끝과 오른쪽 끝이 같은 경우까지 탐색을 했는데 그 값이 key값과 같지 않을 경우 해당 배열에는 key값이 존재하지 않는다는 의미다.

이진 트리 형태의 경우는 거의 대다수가 O(logN)의 시간 복잡도를 갖는다.