백준 2579번
계단 오르기
문제
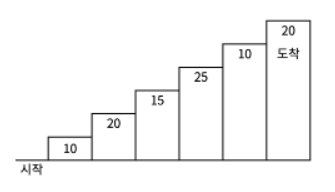
계단 오르기 게임은 계단 아래 시작점부터 계단 꼭대기에 위치한 도착점까지 가는 게임이다. <그림 1>과 같이 각각의 계단에는 일정한 점수가 쓰여 있는데 계단을 밟으면 그 계단에 쓰여 있는 점수를 얻게 된다.
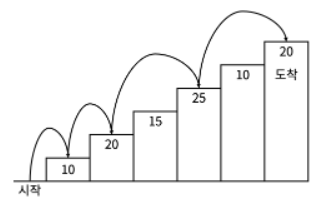
<그림 1>예를 들어 <그림 2>와 같이 시작점에서부터 첫 번째, 두 번째, 네 번째, 여섯 번째 계단을 밟아 도착점에 도달하면 총 점수는 10 + 20 + 25 + 20 = 75점이 된다.
<그림 2>계단 오르는 데는 다음과 같은 규칙이 있다.
- 계단은 한 번에 한 계단씩 또는 두 계단씩 오를 수 있다. 즉, 한 계단을 밟으면서 이어서 다음 계단이나, 다음 다음 계단으로 오를 수 있다.
- 연속된 세 개의 계단을 모두 밟아서는 안 된다. 단, 시작점은 계단에 포함되지 않는다.
- 마지막 도착 계단은 반드시 밟아야 한다.
따라서 첫 번째 계단을 밟고 이어 두 번째 계단이나, 세 번째 계단으로 오를 수 있다. 하지만, 첫 번째 계단을 밟고 이어 네 번째 계단으로 올라가거나, 첫 번째, 두 번째, 세 번째 계단을 연속해서 모두 밟을 수는 없다.
각 계단에 쓰여 있는 점수가 주어질 때 이 게임에서 얻을 수 있는 총 점수의 최댓값을 구하는 프로그램을 작성하시오.
입력
입력의 첫째 줄에 계단의 개수가 주어진다.
둘째 줄부터 한 줄에 하나씩 제일 아래에 놓인 계단부터 순서대로 각 계단에 쓰여 있는 점수가 주어진다. 계단의 개수는 300이하의 자연수이고, 계단에 쓰여 있는 점수는 10,000이하의 자연수이다.
출력
첫째 줄에 계단 오르기 게임에서 얻을 수 있는 총 점수의 최댓값을 출력한다.
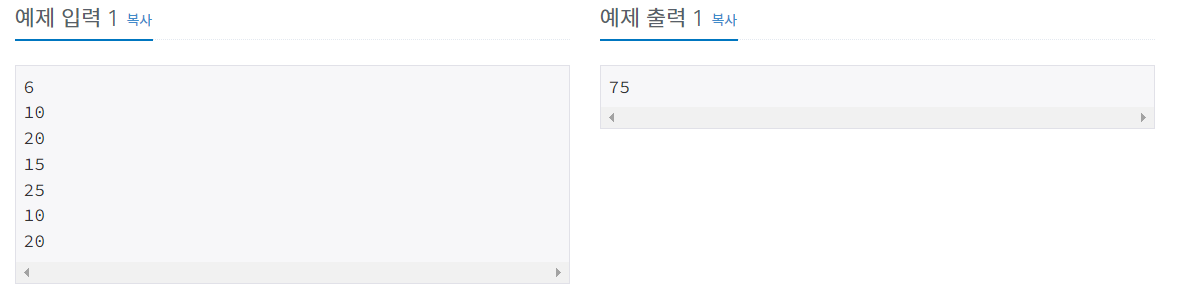
예제
알고리즘 분류
- 다이나믹 프로그래밍
코드
import java.io.*;
public class Main {
static Integer dp[];
static int arr[];
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(br.readLine());
dp = new Integer[N+1];
arr = new int[N+1];
for(int i=1; i<=N; i++)
arr[i] = Integer.parseInt(br.readLine());
dp[0] = arr[0];
dp[1] = arr[1];
if(N>=2)
dp[2] = arr[1] + arr[2];
System.out.println(stairFunc(N));
}
public static int stairFunc(int N) {
if(dp[N] == null)
dp[N] = Math.max(stairFunc(N-2), stairFunc(N-3) + arr[N-1]) + arr[N];
return dp[N];
}
}풀이
이 문제의 경우, DP (Dyamic Programming)으로 해결한다.
DP 해결 법에는, Top-Down 방식과 Bottom-Up 두가지 방법이 모두 적용 될 수 있는데, 주로 Top-Down 방식은 재귀가 사용되고, Bottom-Up 방식은 반복문아 사용된다.
위 문제에서는, 재귀가 사용된 Top-Down 방식의 DP를 활용했다.우선, null 검사를 위해 dp 배열은 int가 아닌, 래퍼 클래스인 Integer 형식으로 정의하였다.
if(N>=2)
dp[2] = arr[1] + arr[2];위 코드는 N이 만약 2가 입력됬을 때, 아래 점화식의 N-3에서 에러를 일으킬 것이므로 추가로 작성한 조건이다.
dp[N] = Math.max(stairFunc(N-2), stairFunc(N-3) + arr[N-1]) + arr[N];위 코드가 점화식으로, 이번 과제의 규칙과 같은 것이다.
1칸 갔다가 두번 뛰어서 3칸 간 경우와 2칸만 간 경우 둘 중 최댓값을 구해주는 방식이다.
이 때, N-1의 경우 stairFunc(N-1)을 더한 것이 아닌, arr[N-1]을 직접 더했는데, 이 이유는 만약 N-1도 stairFunc에 넣어 재귀시켰다면, 계속 N-1의 계단을 밟는 경우도 포함이 되어, 조건(3연속 한칸 내려가는거 불가능)에 위반되는 경우도 고려가 된다는 것이다. 따라서 규칙위반의 위험이 없는 N-2와 N-3만 재귀를 활용하고, N-1은 단순히 그 점수를 더해주는 방식이다. (이게 처음에 이해하기 엄청 어려웠다.)