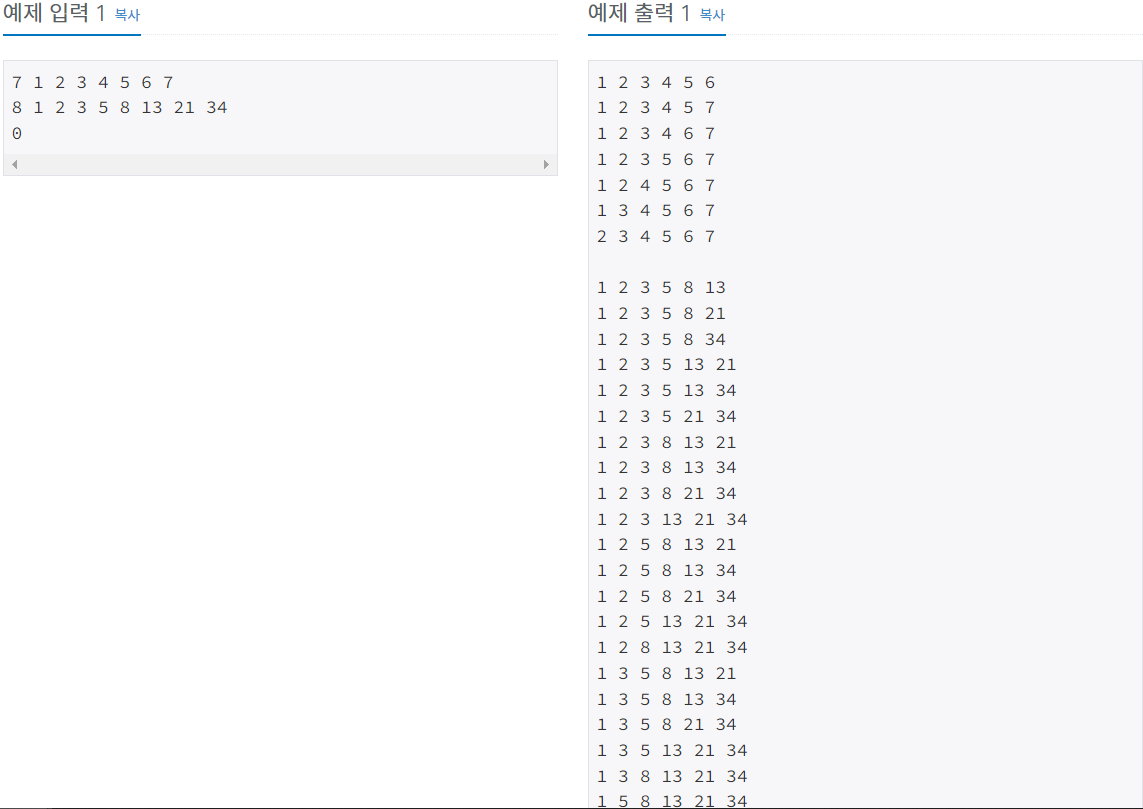
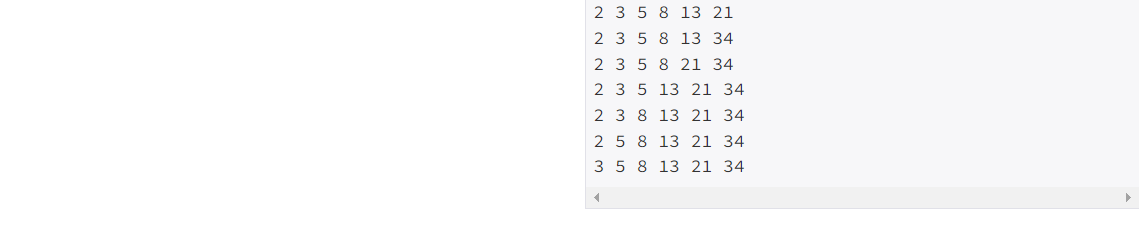
백준 6603번

로또

문제

독일 로또는 {1, 2, ..., 49}에서 수 6개를 고른다.

로또 번호를 선택하는데 사용되는 가장 유명한 전략은 49가지 수 중 k(k>6)개의 수를 골라 집합 S를 만든 다음 그 수만 가지고 번호를 선택하는 것이다.

예를 들어, k=8, S={1,2,3,5,8,13,21,34}인 경우 이 집합 S에서 수를 고를 수 있는 경우의 수는 총 28가지이다. ([1,2,3,5,8,13], [1,2,3,5,8,21], [1,2,3,5,8,34], [1,2,3,5,13,21], ..., [3,5,8,13,21,34])

집합 S와 k가 주어졌을 때, 수를 고르는 모든 방법을 구하는 프로그램을 작성하시오.

입력

입력은 여러 개의 테스트 케이스로 이루어져 있다. 각 테스트 케이스는 한 줄로 이루어져 있다. 첫 번째 수는 k (6 < k < 13)이고, 다음 k개 수는 집합 S에 포함되는 수이다. S의 원소는 오름차순으로 주어진다.

입력의 마지막 줄에는 0이 하나 주어진다.

출력

각 테스트 케이스마다 수를 고르는 모든 방법을 출력한다. 이때, 사전 순으로 출력한다.

각 테스트 케이스 사이에는 빈 줄을 하나 출력한다.

예제

알고리즘 분류

• 수학
• 조합론
• 백트래킹
• 재귀

코드

import java.util.*;
import java.io.*;

public class Main {
	public static int k;
	public static int[] S;
	public static boolean[] visited;
	
	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		StringTokenizer st;
		
		while(true) {
			st = new StringTokenizer(br.readLine(), " ");
			
			k = Integer.parseInt(st.nextToken());
			
			if(k == 0)
				break;
			
			S = new int[k];
			visited = new boolean[k];
			
			for(int i=0; i<k; i++) 
				S[i] = Integer.parseInt(st.nextToken());
			
			DFS(0, 0);
			System.out.println();
		}
	}
	
	public static void DFS(int start, int depth) {
		if(depth == 6) {
			for(int i=0; i<k; i++) {
				if(visited[i])
					System.out.print(S[i] + " ");
			}
			System.out.println();
		}
		
		for(int i=start; i<k; i++) {
			visited[i] = true;
			DFS(i+1, depth+1);
			visited[i] = false;
		}
	}
}

풀이

전형적인 DFS 문제이다. visited 배열을 활용하여 중복되는 것을 막아준다. start 변수를 이용하여 탐색 시작 지점을 쓸데 없는 곳을 피하도록 해준다.

6가지 수를 고르고, 그 경우들 중 visited 배열이 true인 경우만 출력한다.