하노이 탑 알고리즘

문제 정의

3개의 막대 중 하나의 막대에 쌓여 있는 원반을 다른 막대에 그대로 옮기는 문제

규칙

1. 원반은 한 번에 한 개씩만 옮길 수 있음
2. 원반을 쌓을 때는 큰 원반 위에 작은 원반을 올려야 함 (작은 원반 위에 큰 원반 X)

문제 접근

원반이 n개 주어졌을 때 "맨 아래 원반" (n번째 원반)과 "나머지 원반의 묶음" (1,2,...,n-1) 두 분류로 나눠서 봐야 한다

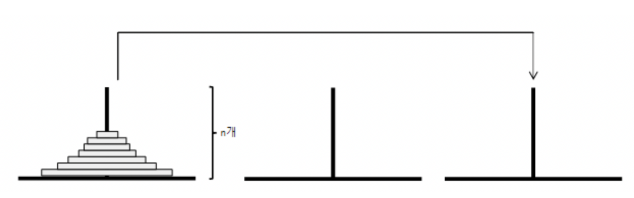
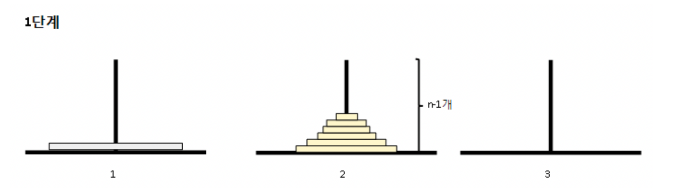1단계: 1번부터 n-1번째 원반을 1번 막대에서 2번 막대로 옮긴다.

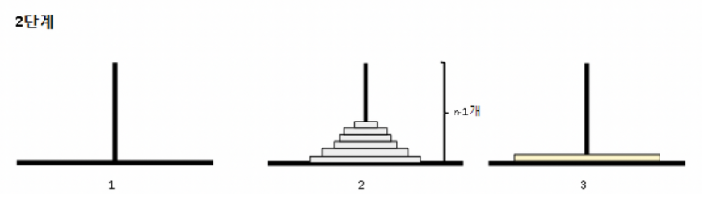2단계: 남은 n번째 원반을 1번에서 3번 막대로 옮긴다.

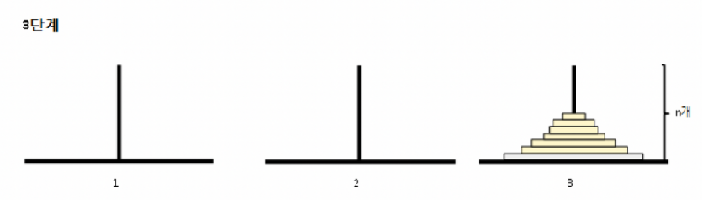3단계: 1번부터 n-1번째 원반을 2번 막대에서 3번 막대로 옮긴다.

총 3가지 단계를 재귀적으로 생각해봐야 한다.

문제 풀이

hanoi 함수: 재귀 함수
move 함수: 원반을 실제로 옮기는 역할, 문제의 추가 요구사항에 따라 옮기는 과정을 출력하거나 옮긴 횟수를 세기 위함

N개의 원반을 start에서 via를 거쳐 to로 옮겨야 하는 경우를
hanoi(N, start, to, via)로 표현할 수 있다.

hanoi(N, start, to, via){
	if(N == 1)
    	move(1, start, to)
    else{
    	hanoi(N-1, start, via, to) //1단계
        move(N, start, to) //2단계
        hanoi(N-1, via, to, start) //3단계
    }
}

hanoi 함수를 코드로 표현해보면 이와 같다.

---

자료 출처

'하노이의 탑' 이해하기 (feat.재귀 함수)