Not Only Rewards But Also Constraints: Applications on Legged Robot Locomotion
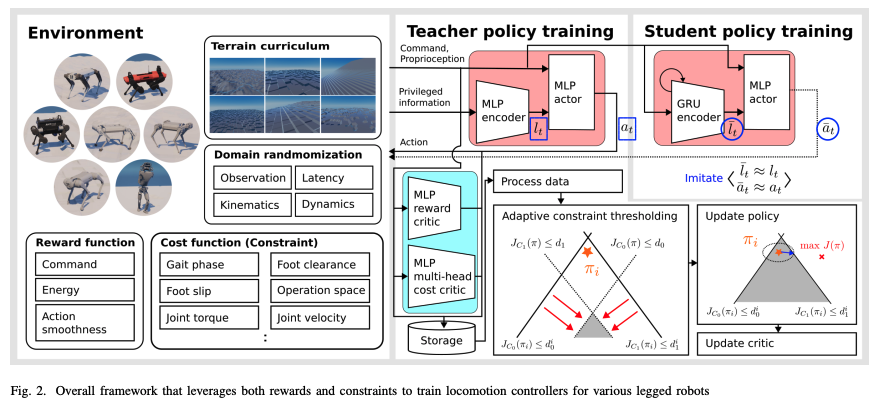
Paper: https://arxiv.org/abs/2308.12517
Constrained RL에 관한 내용으로, 논문에 포함되어 있는 Teacher-Student Learning, Parameterized Terrains, Domain Randomization 내용은 생략되었습니다.
Model-Free RL
-
정의:
모델 프리 강화 학습(Model-Free Reinforcement Learning)은 환경의 물리적 모델(운동 방정식, 다이나믹스 등)을 미리 알 필요 없이, 관찰값(observations)과 보상(rewards)만을 사용하여 정책(policy)을 학습하는 방법.
-
어떻게 작동하나?
-
에이전트(Agent)가 현재 상태(state)를 관찰.
-
행동(action)을 선택하여 환경에 영향을 줌.
-
환경으로부터 새로운 상태와 보상 피드백을 받음.
-
보상을 최대화하는 방향으로 정책을 업데이트.
-
-
특징
-
모델 기반 RL(환경의 동역학 모델을 사용)과 달리, 환경의 내부 모델을 설계할 필요가 없음.
-
대신, 많은 상호작용 데이터가 필요하며 학습 안정성을 유지하기 위해 추가적인 기법(예: 보상 설계, 제약 조건)이 필요.
-
Model-Based RL
-
환경의 물리적 모델(운동 방정식, 다이나믹스 등)을 이용하여 에이전트가 환경을 탐색하는 대신 행동을 시뮬레이션으로 예측.
-
학습 과정:
-
데이터 수집 (실제 환경 상호작용)
- 초기에는 에이전트가 실제 환경과 상호작용하며 데이터를 수집합니다.
- 이 데이터는 (상태, 행동, 보상, 다음 상태) 형태로 저장됩니다.
-
환경 모델 학습
-
수집한 데이터를 기반으로 환경 모델을 학습합니다.
-
목표는 상태-행동 쌍으로부터 다음 상태와 보상을 정확히 예측하는 것입니다.
-
-
가상 시뮬레이션 데이터 생성
- 학습된 환경 모델을 활용해, 에이전트가 실제 환경과 상호작용하지 않아도 가상의 데이터(상태, 행동, 보상, 다음 상태)를 생성합니다.
-
정책 네트워크 학습
-
가상 데이터로 정책을 최적화합니다.
-
최적화 과정은 보상을 최대화하는 방향으로 진행됩니다.
-
-
실제 환경에서 테스트 및 업데이트
- 학습된 정책을 실제 환경에서 테스트하여 성능을 평가하고, 새 데이터를 수집하여 환경 모델과 정책을 반복적으로 개선합니다.
-
강화학습이 로봇 시스템에서 중요한 이유
-
전문가 시범 데이터의 제한성 → Motion, AMP
-
로봇 시스템에서 필요한 데이터를 수집하기 위해 전문가의 시범 데이터를 얻는 것은 어렵고, 제한적인 경우가 많음.
-
반면, 물리 시뮬레이션이나 실제 실험을 통해 상호작용 데이터를 쉽게 얻을 수 있음.
-
-
강화학습의 장점
-
상호작용 데이터를 기반으로 학습하는 강화학습은 모델 기반 접근법보다 적합.
-
특히 아래와 같은 경우에서 더 강력한 성능을 발휘:
-
접촉면이 많은 시스템 : 다족 로봇, 높은 자유도의 로봇 손처럼 복잡한 움직임이 요구되는 경우.
-
환경적 불확실성이 큰 경우 : 센서 노이즈나 외부 방해 요소가 많은 상황에서도 유연하게 동작 가능.
-
-
엔지니어가 강화학습으로 신경망 제어기를 개발할 때 일반적으로 다음 단계를 따릅니다.
-
관측 및 행동 공간에 기반하여 귀납적 편향이 있는 신경망 구조를 설계한다.
-
환경 상호작용 시나리오를 풍부하게 생성한다(예: 다족 로봇 운동을 위한 랜덤 지형, 로봇 손 그리핑을 위한 다양한 물체 메쉬).
-
로봇의 물리적 제약 조건(예: 관절 토크 및 속도 제한)을 충족하고 자연스러운 움직임 스타일을 가지는 고성능 제어기를 얻을 때까지 보상 항목을 설계하고 보상 계수를 조정한다.
이 세 단계 중 마지막 단계는 반복적인 조정 과정이 필요하기 때문에 가장 시간이 많이 소요됩니다. 특히 보상 항목이 10개 이상인 경우, 각각의 보상 항목 가중치를 로봇 움직임의 결과를 기준으로 찾는 일은 간단하지 않습니다.
수많은 보상 항목을 설계하고 적절한 보상 계수를 결정하는 데 많은 시간과 노력이 요구되는 보상 엔지니어링 과정을 거쳐야만 개발됩니다.
본 연구에서는 다음과 같은 근본적인 질문을 제기하고자 합니다:
왜 제약 조건을 강화학습에 활용하지 않았는가?
-
강화학습의 본질
-
강화학습은 수치 최적화 문제로 볼 수 있음:
- 목표는 보상 항목들의 가중합을 최대화하는 신경망 매개변수를 찾는 것.
-
시스템이 복잡할수록, 보상 엔지니어링을 통해 최적화 과정의 문제를 해결하려고 함.
-
-
보상 엔지니어링의 한계
-
복잡한 시스템과 민첩한 동작을 위해서는 보상 항목(10개 이상인 경우도 많음)을 설계하고 가중치를 조정해야 함.
-
이 과정은 시간이 많이 들고, 국소 최적점(local optima) 문제를 해결하기 어렵다는 단점이 있음.
-
-
제약 조건의 필요성
-
수치 최적화 문제에서는 제약 조건을 활용해 해결 공간을 제한하는 것이 효과적.
-
제약 조건을 사용하면 바람직하거나 실제로 가능한 영역으로 탐색 공간을 좁힐 수 있음.
-
하지만 기존 강화학습에서는 제약 조건을 명시적으로 활용하지 않아 비효율적인 접근이 이루어짐.
-
제약 조건을 활용한 강화학습 프레임워크의 이점
-
일반화 가능성 향상
-
보상만으로 설계된 학습 프레임워크는 로봇마다 보상 신호의 차이로 인해 성능이 달라질 수 있음.
-
반면, 제약 조건은 로봇 플랫폼이 달라져도 일관되게 적용 가능:
- 예: 보행 패턴 제약(트로팅 게이트)을 사용하면 로봇의 크기, 무게, 모양과 관계없이 모든 4족 로봇에 적용 가능.
-
-
단순하고 효율적인 설계
-
보상 항목 수를 줄일 수 있어 엔지니어링 과정이 단순화됨.
-
예: 하드웨어 한계(관절 각도 제한 등)나 동작 스타일을 정의하기 위해 추가했던 보상 항목들이 더 이상 필요하지 않음.
-
대신, 제약 조건으로 명확히 정의하여 학습 정책을 엔지니어 의도에 맞게 유도 가능.
-
-
제약 조건은 물리적 의미를 가지므로 직관적으로 설정 가능:
- 예: URDF 파일에서 자동으로 추출된 로봇의 관절 제한값.
-
제안된 강화학습 프레임워크
-
보상 + 제약 조건을 병합
-
기존의 안전 강화학습(Safe RL) 연구에서 영감을 받아, 보상과 제약 조건을 모두 활용하는 강화학습 프레임워크를 제안.
-
제약 조건을 효율적으로 처리할 수 있는 정책 최적화 알고리즘 포함.
-
추가적인 계산 비용은 거의 없으면서도 높은 성능의 정책 학습 가능.
-
-
제약 조건의 일반화와 직관성
-
제약 조건은 보상과 달리 여러 로봇에 일반화 가능하며, 물리적 의미가 있어 설정 과정이 간단하고 명확함.
-
실험적으로는 3개의 보상 항목과 단일 보상 계수 조정만으로 성능 높은 정책을 학습 가능.
-
실험 및 결과
-
여러 로봇 플랫폼 적용
-
제안된 프레임워크를 사용하여 다양한 다족 로봇과 이족 로봇(총 7종)의 보행 제어기를 학습.
-
로봇의 형태(다리 개수, 기계 설계)와 물리적 특성(무게, 액추에이터 특성)이 달라도 효과적으로 동작.
-
-
시뮬레이션 및 실제 환경 실험
- 실험 결과, 제약 조건을 활용한 학습이 보상 엔지니어링만으로는 달성하기 어려운 일반화된 성능과 높은 견고성을 보임.
→ 제약 조건을 보상 엔지니어링을 보완하거나 대체하는 도구로 활용하는 가능성을 보여줌.
로봇 플랫폼이 달라져도 일관되게 적용 가능한 이유
제약 조건은 로봇 플랫폼의 고유 특성(예: 크기, 무게, 관절 구조)에 의존하지 않고 일반적인 조건으로 설정되기 때문입니다.
-
예를 들어, 4족 로봇의 트로팅 게이트(다리를 교차로 움직이는 보행 패턴)는 모든 4족 로봇에서 유효합니다.
-
트로팅은 다리 움직임의 순서와 주기만 정의하기 때문에, 로봇의 크기나 무게가 달라도 동일한 패턴을 적용할 수 있습니다.
-
즉, 이 조건은 로봇의 구체적인 물리적 특성을 고려하지 않아도 되므로 범용적입니다.
-
반대로 보상으로 트로팅 동작을 유도하려면, 로봇마다 다를 수 있는 다음과 같은 세부 정보를 고려해야 합니다:
-
각 다리가 얼마나 "잘 움직이는지"를 측정하는 기준
-
로봇마다 다른 관절 속도, 관절 위치, 힘 등 피드백 신호
이러한 이유로, 보상을 설계하는 과정은 로봇마다 달라지고 복잡해집니다.
제약 조건이 보상보다 엔지니어링이 덜 필요한 이유
-
제약 조건은 물리적/기술적 제한을 직접 명시
-
제약 조건은 로봇의 제한사항을 명확하게 정의합니다.
- 예: 관절 각도 제한, 힘 출력 범위 등.
-
이런 조건들은 물리적 의미를 가지며 직관적으로 설정 가능합니다.
- URDF 파일(로봇 모델 파일)에서 자동으로 불러올 수도 있어 엔지니어가 따로 설계할 필요가 없습니다.
-
-
보상 설계는 비선형적이고 로봇 특성에 의존적
-
보상은 특정 동작을 유도하기 위한 수학적 모델링입니다.
-
보상 항목마다 중요도를 조정하는 가중치(계수)를 설정해야 하며, 이는 실험적으로 조정해야 하는 경우가 많습니다.
- 예: R=w1⋅속도+w2⋅힘 절약+w3⋅균형 유지 R=w1⋅속도+w2⋅힘 절약+w3⋅균형 유지
- 예: R=w1⋅속도+w2⋅힘 절약+w3⋅균형 유지 R=w1⋅속도+w2⋅힘 절약+w3⋅균형 유지
-
로봇마다 신호가 다르기 때문에 이 가중치를 일일이 조정하는 작업은 시간과 노력이 많이 듭니다.
-
-
제약 조건으로 보상을 대체하면 설계 간소화
-
보상에서 "소프트 페널티"로 처리하던 것(예: 특정 동작을 하지 않으면 점수를 감점)을 제약 조건으로 "하드 제한"으로 정의하면,
- 보상 항목이 줄어듦 → 조정해야 할 변수 감소.
- 최적화가 제약 조건 내부에서 이루어져, 정책 학습이 더 간단해짐.
-
예시
보상으로 트로팅 게이트 유도
-
네 다리가 교차로 움직이도록 하기 위해 다음을 보상에 포함:
-
속도: 다리 움직임 속도가 트로팅 동작과 얼마나 가까운지.
-
균형: 로봇이 넘어지지 않고 중심을 유지하는지.
-
힘 절약: 불필요한 에너지를 소비하지 않는지.
-
-
이 모든 보상 항목에 적절한 계수를 찾기 위해 실험적으로 수많은 조정을 해야 함.
제약 조건으로 트로팅 게이트 설정
-
네 다리의 움직임 패턴을 수학적 제약으로 정의:
- 예: 왼쪽 앞다리와 오른쪽 뒷다리가 같은 주기로 움직임.
-
이 조건은 로봇의 물리적 특성에 관계없이 일괄 적용 가능하며, 실험적 조정이 필요 없음.
결론
-
제약 조건은 로봇의 특정 특성과 무관한 일반화된 규칙으로 설정되므로 로봇 플랫폼이 달라져도 동일하게 적용 가능.
-
보상을 통해 원하는 행동을 유도하려면 복잡한 조정과 실험적 튜닝이 필요하지만, 제약 조건은 물리적 의미가 명확해 직관적이고 자동화된 설정이 가능.
-
따라서 제약 조건을 추가하면 엔지니어링 부담이 줄어듦.
제약 조건 vs 모델의 자율 학습
-
제약 조건을 사용하는 이유
제약 조건을 추가하면:
-
인간의 지식을 활용하여 모델의 학습을 유도.
-
학습의 불안정성을 줄이고 더 빠르게 수렴할 수 있음.
-
특히 데이터가 부족하거나 복잡한 환경에서는 제약 조건이 학습의 가이드를 제공.
-
-
모델이 직접 학습하도록 두는 접근의 한계
-
데이터 부족: 4족 로봇의 실제 환경 데이터를 많이 얻는 것은 비용과 시간이 많이 듬.
-
학습 불안정성: 보상 설계가 잘못되거나 초기 학습 과정에서 잘못된 행동을 학습할 가능성.
-
복잡한 환경에서의 일반화: 로봇마다 다르게 설계된 하드웨어(모르포로지)를 고려해야 해서 완전 자율 학습은 어려움.
-
즉, 제약 조건은 초기 학습의 안정성과 효율성을 제공하지만, 완전히 새로운 방법을 발견하는 데는 제약이 될 수 있음. 연구자들은 보상과 제약 조건을 조화롭게 설계하여 이 문제를 해결하려고 함.
Constrained Reinforcement Learning
1. 강화 학습과 제약 조건의 필요성
-
일반적인 강화 학습에서는 에이전트가 보상(reward)을 최대화하기 위해 학습함.
-
하지만 로봇 제어와 같은 현실적인 문제에서는 에이전트가 무제한으로 행동할 수 없음:
-
예: 로봇의 몸체가 지면에 닿지 않도록 하거나, 관절의 속도를 하드웨어 한계 내로 제한.
-
탐색 공간(search space)을 유도하여 안정적이고 안전한 학습이 필요함.
-
2. CMDP(Constrained Markov Decision Process) 프레임워크
-
CMDP는 강화 학습에서 제약 조건을 처리하기 위한 수학적 모델.
-
에이전트가 보상을 최대화하면서 제약 조건을 만족해야 함.
-
제약 조건은 보통 비용 함수(cost terms)의 기대값 형태로 정의됨.
-
3. 제약 조건 적용 방법
제약 조건을 처리하는 방법은 두 가지로 분류됨:
-
최적화 기준(Optimization Criterion)
- 정책을 업데이트하면서 제약 조건을 만족하도록 학습.
-
탐색 과정(Exploration Process)
- 학습 중 안전하지 않은 상태에서 안전 정책(safe policy)으로 개입.
현재 연구의 초점:
- 시뮬레이션 환경에서 학습하므로 최적화 기준 방법에 집중.
- 안전한 탐색을 위한 개입은 중요하지 않음.
4. 최적화 기준 방법
최적화 기준 방법은 정책을 업데이트하는 방식에 따라 두 가지로 나뉨:
-
Lagrangian 방법
-
라그랑주 승수를 사용해 제약 조건을 비제약 문제로 변환.
-
장점: 제약 조건이 만족되도록 학습 가능.
-
단점: 하이퍼파라미터(라그랑주 승수 초기화 등)에 민감하고 학습이 불안정.
-
-
Trust-Region 방법
-
제약 조건과 보상을 선형 근사하여 안전한 정책 업데이트를 수행.
-
1차 및 2차 방법으로 나뉨:
-
1차 방법: 제약 조건을 비제약 문제로 변환해 1차 미분만 사용.
- 예: IPO(Interior-point Policy Optimization), P3O(Penalized Proximal Policy Optimization).
-
2차 방법: 2차 미분 사용.
- 예: CPO(Constrained Policy Optimization).
-
-
5. 주요 알고리즘 및 연구
-
CPO (Constrained Policy Optimization)
-
제약 조건을 선형 근사화한 2차 미분 기반 알고리즘
-
장점: 정책이 단조롭게 개선(monotonic improvement)
-
단점: 2차 미분 계산 부담
-
-
IPO (Interior-point Policy Optimization)
-
로그 장벽 함수(logarithmic barrier functions)를 사용해 제약 조건을 만족하도록 학습
-
장점: 1차 미분만 사용하므로 계산 효율성이 높음
-
단점: 제약 조건이 많아지면 학습이 어려워질 수 있음
-
-
P3O (Penalized Proximal Policy Optimization)
-
제약 조건 위반 시 선형 비용 페널티를 부과
-
제약 조건이 만족되면 비용 페널티를 무시
-
6. 개선된 알고리즘
이 논문에서는 IPO를 기반으로 여러 가지 개선점을 추가하여 다중 제약 조건에 대응할 수 있는 방법을 제안:
-
적응형 제약 임계값 설정
- 현재 정책 성능에 따라 제약 조건 임계값을 조정하여 효율적으로 제약 조건을 만족
-
다중 헤드 비용 함수(Multi-Head Cost Value Function)
- 메모리 효율적으로 다중 비용 함수와 비용 이점을 병렬로 계산
이전 연구와의 주요 차이점:
-
제약 조건을 보상으로 처리하지 않아 비용 설계의 필요성 감소.
-
참조 궤적(reference trajectory) 없이 간단한 보상 설계만으로도 학습 가능.
CMDP(Constrained Markov Decision Process)
CMDP는 제약 조건이 있는 강화 학습 문제를 정의하기 위한 확장된 MDP(Markov Decision Process) 프레임워크입니다. 이를 이해하기 위해, CMDP의 구성 요소와 수식 및 해결 방법을 정리합니다.
1. CMDP의 정의
CMDP는 다음과 같은 구성 요소로 정의됩니다:

2. 정책의 성능 지표
보상 기대값 J(π)
정책 π에 따른 누적 보상의 기대값을 정의:
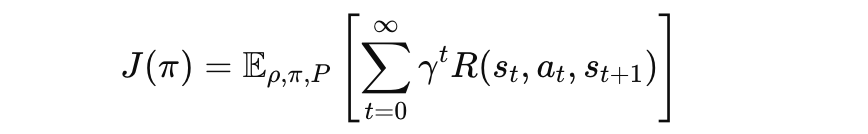
- R(st,at,st+1) : 시뮬레이션 환경에서 주어지는 보상 함수. 특정 상태 st에서 행동 at를 수행했을 때, 다음 상태 st+1로 전이되면서 얻는 보상입니다.
- gamma γ : 할인율로, 미래 보상의 중요도를 조정합니다 (0≤γ<1).
- ρ : 초기 상태 분포로 시뮬레이션 시작 시 상태 s0의 분포입니다.
- P(s′∣s,a) : 상태 전이 확률로, 현재 상태 s에서 행동 a를 했을 때 s′로 전이될 확률입니다.
시뮬레이션 환경에서의 계산
-
보상 함수 정의: 시뮬레이션 환경에 맞는 보상 R(s,a,s′)를 설정합니다. 예를 들어, 로봇 제어 문제에서는 다음이 포함될 수 있음:
- 이동 목표를 성공적으로 달성했는가 +100
- 충돌 발생 시 패널티 -50
- 행동의 에너지 소모 비용 -1
-
에피소드 실행 : 정책 π를 사용해 시뮬레이션 환경에서 여러 에피소드를 실행하며 각 t에서 R(st,at,st+1) 값을 수집합니다.
-
누적 보상 계산 : 한 에피소드에서 누적 보상을 계산한 후, 여러 에피소드의 평균으로 J(π)를 추정합니다:
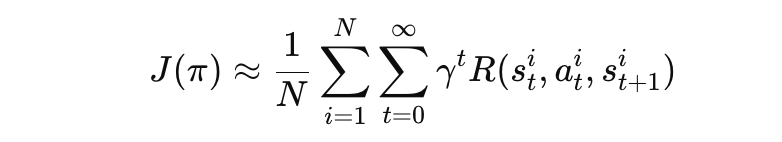
비용 기대값 J_{C_k}(π)
제약 조건 비용 함수 Cₖ에 대한 기대값:
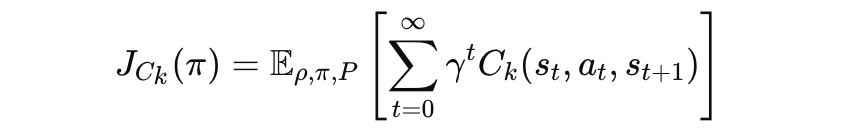
Ck(s_t, a_t, s{t+1}) : 특정 제약 조건에 해당하는 비용 함수입니다.
- 예: 로봇이 에너지를 과다 소비하거나 충돌할 때의 비용.
시뮬레이션 환경에서의 계산
-
비용 함수 정의:
제약 조건을 기반으로 비용을 설정합니다.예를 들어:
- 충돌 발생 비용 +10
- 에너지 소비 비용 +0.1 × 사용에너지
-
에피소드 실행 및 비용 수집:
보상과 유사하게, 정책 π를 기반으로 시뮬레이션을 진행하며 각 t에서 비용 함수 Ck(s_t, a_t, s{t+1}) 값을 수집합니다.
-
누적 비용 계산:
한 에피소드에서 누적 비용을 계산한 후, 여러 에피소드의 평균으로 J_{C_k}(π)를 추정합니다:
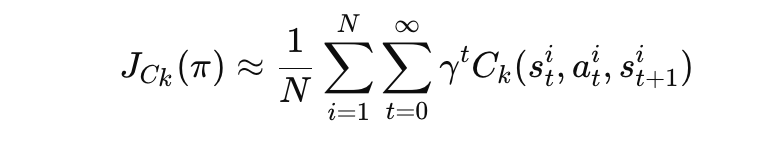

3. CMDP에서의 강화 학습 문제 정의
강화 학습에서의 목표는 다음과 같음:
- 보상 기대값 J(π)을 최대화.
- 비용 기대값 J_{C_k}(π) 이 각 제약 조건 dₖ을 초과하지 않도록 학습.
수식으로 표현하면:
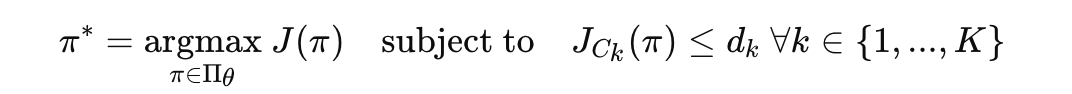
Π_θ : 파라미터 θ로 정의된 정책 집합.
dₖ : 각 제약 조건의 임계값.
4. 신뢰 영역(Trust Region) 내의 근사
CMDP 문제를 효율적으로 해결하기 위해, 신뢰 영역 내에서 문제를 근사화함.
Achiam et al.(2017)의 도출에 따르면, CMDP는 다음과 같이 변환됨:
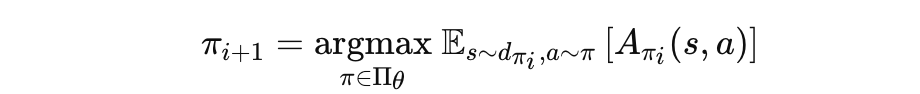
제약 조건:
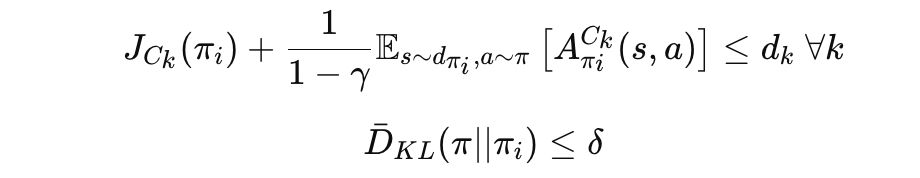
- A_{π_i}(s, a) : 보상 이점 함수(Reward Advantage Function)
- A_{π_i}^{C_k}(s, a) : 비용 이점 함수(Cost Advantage Function)
- bar{D}_{KL}(π || π_i) : 신뢰 영역 내 KL 발산(KL Divergence)
- δ : 최대 업데이트 크기.
5. 주요 개념 설명
-
이점 함수(Advantage Function)
-
현재 정책 π_i에서 상태-행동 쌍의 이점(advantage)을 계산해 업데이트 방향 설정.
-
보상 이점: A_{π_i}(s, a)
-
비용 이점: A_{π_i}^{C_k}(s, a)
-
-
신뢰 영역(Trust Region)
- 정책 업데이트가 안정적으로 이루어지도록 KL 발산의 범위를 제한.
-
다양한 알고리즘 적용 가능
- CPO, IPO 등 CMDP 문제를 해결하기 위해 여러 알고리즘이 사용됨.
6. 결론
-
CMDP는 보상과 제약 조건을 동시에 만족시키는 정책 학습을 가능하게 함.
-
신뢰 영역을 활용해 안전하고 안정적인 정책 업데이트가 가능.
-
CMDP 기반 강화 학습은 로봇 제어와 같이 다중 제약 조건이 요구되는 환경에서 유용함.
IV. LEARNING FRAMEWORK
A. Constraint Types
(1) 확률적 제약 (Probabilistic Constraints)
확률적 제약은 특정 원하지 않는 사건(undesirable event)이 발생할 확률을 제한하는 방식입니다. 이 방식에서는 확률적으로 로봇의 행동을 제어하여, 원하지 않는 이벤트가 발생할 확률이 일정 수준 이하로 떨어지도록 합니다.
-
비용 함수 정의: 확률적 제약은 먼저 비용 함수 C_k(s, a, s')를 지표 함수(indicator function)로 정의합니다. 지표 함수는 상태 s, 행동 a, 결과 상태 s'가 특정 조건을 만족하는지 여부를 확인하는 함수입니다.
예를 들어, 로봇의 중심 위치가 특정 높이 이하로 떨어지는 것을 방지하고자 할 때, 그 조건을 지표 함수로 설정할 수 있습니다.
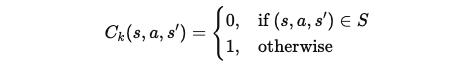
S는 원하는 상태 공간(desirable event space)이고, C_k(s, a, s')는 이 상태가 S에 포함될 때 0, 포함되지 않으면 1로 설정됩니다.



-
확률 제약 설정: 이렇게 설정된 지표 함수는 확률적 제약으로 변환됩니다. 제약은 원하지 않는 사건이 발생할 확률이 일정 값 D_k 이하가 되도록 제한하는 방식입니다. D_k는 확률 제약을 만족해야 하는 임계값입니다.
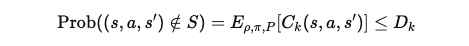
여기서 D_k in [0, 1]는 kth 제약에 대한 확률 임계값입니다. D_k = 0일 경우, 정책은 원하지 않는 사건을 절대 발생시키지 않도록 학습해야 합니다. 하지만 확률적 MDP에서는 이 제약을 완전히 만족시키는 것은 어려울 수 있으므로, D_k는 보통 아주 작은 값으로 설정됩니다.
-
적용 예시: 로봇의 중심 위치가 일정 거리 이하로 떨어지는 것을 방지하려면, 중심 위치의 원하는 범위 S를 정의하고, 확률 제약을 설정하여 로봇이 그 범위 내에서만 행동하도록 유도할 수 있습니다.
(2) 평균 제약 (Average Constraints)
평균 제약은 로봇의 물리적 변수가 주어진 임계값 이하로 유지되도록 제한하는 방식입니다. 이는 특정 시점에서 제약을 만족시키는 것이 아니라, 전체 에피소드 동안의 평균이 주어진 임계값을 초과하지 않도록 하는 제약입니다.
-
비용 함수 정의: 평균 제약은 비용 함수 C_k(s, a, s')를 해당 물리적 변수를 반영하는 함수로 정의합니다. 예를 들어, 로봇의 발의 속도가 일정 수준 이하로 유지되어야 한다면, 발 속도를 물리적 변수로 설정할 수 있습니다.
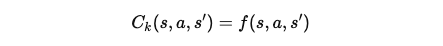
f(s, a, s')는 물리적 변수, 예를 들어 발 속도와 같은 값을 정의하는 함수입니다.
-
평균 제약 설정: 이 경우 제약은 전체 에피소드 동안의 평균 값이 임계값 D_k를 초과하지 않도록 제한됩니다. 즉, 물리적 변수의 평균 값이 주어진 임계값 이하로 유지되도록 요구합니다.
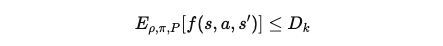
이 제약은 로봇의 특정 물리적 변수에 대한 평균 제약을 설정하는 데 사용됩니다.
-
적용 예시: 예를 들어, 발의 속도가 너무 빠르면 미끄러지거나 불안정한 움직임이 발생할 수 있습니다. 이때 발의 속도가 너무 빠르지 않도록 제한하는 평균 제약을 설정할 수 있습니다.
B. Policy optimization
1. 문제 정의: 제약 조건이 있는 정책 최적화
- 목표: 주어진 보상 J(pi)을 최대화하는 최적의 정책 pi를 찾는다.
- 추가 조건: 정책은 제약 조건 J_{C_k}(pi) ≤ d_k 를 만족해야 한다.
J_{C_k}(pi) : 시간에 따라 누적된 제약 비용.
d_k : 제약 조건의 상한.
2. 제약 조건 누적 계산
제약 조건은 단순히 하나의 상태에서 만족하는 것이 아니라, 시간에 걸쳐 누적 비용으로 계산됩니다.
누적 비용의 정의는 다음과 같습니다:
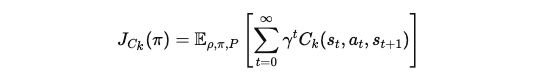
gamma : 할인율, 먼 미래의 비용보다 가까운 비용을 더 중요하게 반영.
C_k(s, a, s') : 특정 상태, 행동, 결과가 제약 조건을 만족하지 않을 때 비용 (예: 충돌 발생 등).
이를 통해 제약 조건을 만족시키는 정책이 점진적으로 학습됩니다.
3. IPO(Interior-Point Policy Optimization) 알고리즘
IPO는 위의 제약 조건 문제를 비제약 문제로 변환합니다. 이를 위해 로그 배리어 함수를 사용합니다.
로그 배리어 함수 변환
제약 조건을 만족하지 않으면 큰 페널티를 부과하여 정책이 제약을 충족하도록 만듭니다:
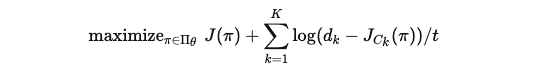
log(dk - J{C_k}(pi)) : 제약 조건에서 얼마나 여유가 있는지를 로그 값으로 나타냄.
t > 0 : 하이퍼파라미터로, 로그 함수의 기울기를 제어함.
- 제약 조건이 충분히 여유가 있다면(즉,dk - J{C_k}(pi)가 큼), 페널티가 작아짐.
- 제약 조건에 가까워지면 페널티가 커져 정책이 이를 피하도록 학습.
4. IPO와 TRPO의 조합
논문에서는 IPO를 기반으로 하되, 제약 조건 학습의 안정성을 높이기 위해 TRPO(Trust Region Policy Optimization)를 사용합니다.
TRPO의 특징:
- 신뢰 영역(Trust Region)을 설정하여 정책이 급격히 변하지 않도록 제어.
- 안정적으로 정책 성능을 개선하면서도 제약 조건을 확인.
변형된 목표 함수
최종적으로 TRPO와 결합한 IPO의 목표 함수는 다음과 같습니다:
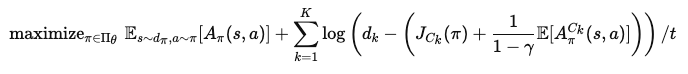
A_pi(s, a) : Advantage 함수, 현재 상태에서 행동이 얼마나 유리한지를 나타냄.
A_pi^{C_k}(s, a) : 제약 조건 비용에 대한 Advantage 함수.
이 목표를 최적화하면서 제약 조건을 준수하는 정책을 학습합니다.
5. 주요 개선 사항
이 논문에서는 기존 IPO 방식의 한계를 개선하기 위해 다음 두 가지를 추가했습니다:
-
대규모 제약 처리: 제약 조건이 많아도 효율적으로 처리할 수 있도록 개선.
-
안정성 향상: TRPO를 사용하여 정책 업데이트 시의 안정성을 높임.
6. 요약
-
IPO: 제약 조건 문제를 로그 배리어 함수로 변환하여 최적화.
-
TRPO 결합: 신뢰 영역 설정으로 정책 학습의 안정성과 제약 조건 만족을 동시에 보장.
-
핵심 아이디어: 제약 조건을 위반하면 큰 페널티를 부여해 정책이 제약 조건 내에서 최적의 행동을 학습하도록 유도.
Algorithm

입력
-
초기 정책 pi_{theta_0} : 학습할 정책
-
가치 함수 V_{phi_0} : 상태-가치 예측을 위한 신경망
-
다중 헤드 비용 가치 함수 V_{ψ_0}^{C1,...,CK} : 각 제약 조건 비용을 예측
출력
- 학습된 최적 정책 pi_{theta_N}
단계 요약
-
Trajectory 샘플링:
- 정책 pi_{theta_n}을 사용하여 상태, 행동, 보상, 제약 비용 데이터를 수집.
-
Advantage 계산:
- 일반 보상에 대한 Advantage A_pi
- 제약 조건 비용에 대한 Advantage A_pi^{C_k}
-
제약 임계값 업데이트:
- Adaptive Constraint Thresholding (d_k^i)를 사용해 제약 조건 임계값 조정.
-
정책 업데이트:
- 로그 배리어 함수 기반으로 정책을 최적화 (IPO + TRPO 결합).
-
가치 함수 업데이트:
- 상태-가치와 다중 헤드 비용 가치 함수를 업데이트.

V. APPLICATIONS ON LEGGED ROBOT LOCOMOTION
학습 과정
1. 시뮬레이션 환경
-
절차적 지형 생성(Parameterized Terrains):
-
다양한 기하학적 구조를 가진 지형을 생성.
-
로봇이 현재 학습 가능한 수준의 난이도를 유지.
-
다양한 지형에서 훈련된 데이터로 로봇의 견고성(Robustness)을 확보.
-
-
도메인 랜덤화(Domain Randomization):
-
현실-시뮬레이션 간 차이를 줄이기 위해 물리적 속성(예: 마찰 계수, 질량)을 무작위로 변동.
-
Sim-to-Real Gap을 극복하기 위한 핵심 기술.
-
2. 교사-학생 학습 과정 (Teacher-Student Learning):
-
교사 정책(Teacher Policy):
-
시뮬레이션 환경에서 고성능 정책 학습.
-
관절 위치, 몸체 자세와 같은 Proprioceptive Sensor 데이터와 Privileged Information(시뮬레이션에서만 얻을 수 있는 정보) 사용.
-
-
학생 정책(Student Policy):
-
교사 정책의 동작을 모방하도록 학습.
-
Proprioceptive Sensor 데이터만 사용.
-
예측 정확도를 높이기 위해 과거 데이터 기반의 압축된 정보(Privileged Information)를 예측.
-
보상(Rewards)과 제약(Constraints)의 통합:
-
기존에는 하드웨어 제약 및 동작 스타일을 보상으로 표현.
-
제안된 방법에서는 이를 명시적 제약(Constraints)으로 처리해 문제를 단순화.
-
보상 항목을 3개로 줄이고도 자연스러운 보행 동작을 생성.
보상

보상 함수 (Reward Function)
- 명령 추적 (Command Tracking):
- 주어진 속도 명령을 얼마나 잘 추적하는지 측정.
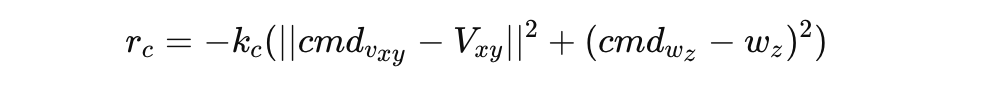
- 관절 토크 최소화 (Joint Torque):rτ=−kτ∣∣τ∣∣2
- 토크 사용량을 최소화.
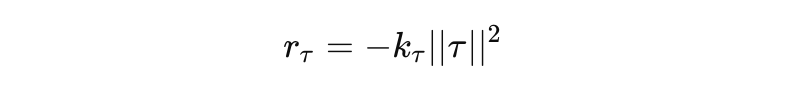
- 행동 부드러움 (Action Smoothness):
- 동작의 부드러움을 유지해 실제 모터 진동 방지.
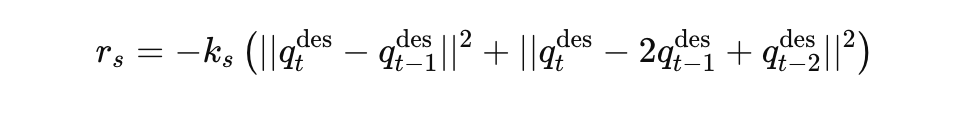
최종 보상:
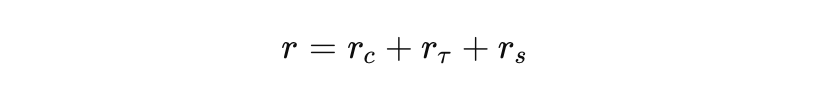
kc, kτ, ks : 각 보상의 가중치.
보상 계수 스케일링
- 로봇의 질량에 따라 토크 보상 계수 (kτ)를 조정:
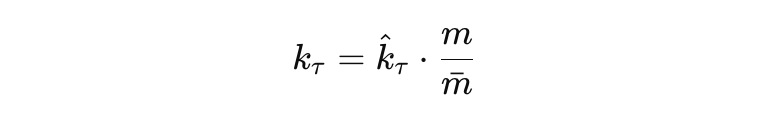
hat{k}_τ : 기준 로봇의 보상 계수.
m, mˉ : 로봇의 실제 질량 및 기준 로봇의 질량.
제약
- Probabilistic Constraints (확률적 제약):
- 비용 함수: 인디케이터 함수 사용.

- 비용 함수: 인디케이터 함수 사용.
- Average Constraints (평균 제약):
- 비용 함수: 물리적 변수 기반으로 직접 정의.
- 예) 속도, 높이 등의 물리적 단위로 직관적 설정 가능.
- 비용 함수: 물리적 변수 기반으로 직접 정의.
확률적 제약 (Probabilistic Constraints)
확률적으로 만족시켜야 할 제약 조건들. 비용 함수는 인디케이터 함수를 사용하여 제약 위반 시 패널티를 부여.
-
Joint Position (cjp):
- 제약 조건: 관절 각도가 유효 범위 내에 있어야 함.
- 비용 함수:

-
Joint Velocity (cjv):
- 제약 조건: 관절 속도가 모터 사양에 맞는 범위 내에 있어야 함.
- 비용 함수:
위와 동일한 방식으로 계산.
-
Joint Torque (cjt):
- 제약 조건: 관절 토크가 모터 사양 범위 내에 있어야 함.
- 비용 함수:
위와 동일한 방식으로 계산.
-
Body Contact (cbc):
- 제약 조건: 발 이외의 로봇 본체가 지면에 닿지 않아야 함.
- 비용 함수:

-
Center of Mass (ccom):
- 제약 조건: 로봇의 무게중심(COM) 높이가 적절한 범위 내에 있어야 하며, 기울기가 안정적이어야 함.
- 비용 함수: 위와 동일한 방식으로 계산.
-
Gait Pattern (cgp):
- 제약 조건: 미리 정의된 발의 접촉 타이밍과 실제 발의 움직임이 일치해야 함.
- 비용 함수:

평균 제약 (Average Constraints)
평균적으로 만족시켜야 할 제약 조건들. 비용 함수는 물리적 변수를 기반으로 정의.
-
Orthogonal Velocity (cov):
- 제약 조건: 명령받은 방향이 아닌 다른 방향의 속도를 최소화.
- 비용 함수:
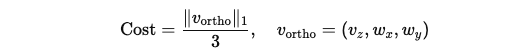
-
Contact Velocity (ccv):
- 제약 조건: 접촉점의 속도가 작아 슬립 방지.
- 비용 함수:
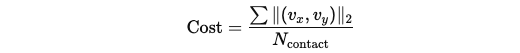
-
Foot Clearance (cfc):
- 제약 조건: 발이 일정 높이 이상으로 올라야 함.
- 비용 함수:
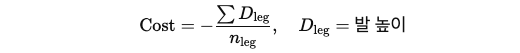
-
Foot Height Limit (cfh):
- 제약 조건: 발 높이가 너무 높아지지 않도록 제한.
- 비용 함수:
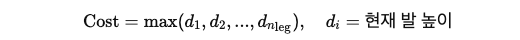
-
Symmetry Constraint (csym):
- 제약 조건: 로봇 동작이 대칭적이어야 함.
- 비용 함수:
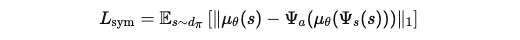
-
총 제약 조건:
- 6개의 확률적 제약
- 5개의 평균 제약
- 대칭 제약 포함 시 총 12개의 제약 조건.
-
제약 만족 여부 판단:
- 확률적 제약: 인디케이터 함수 사용.
- 평균 제약: 물리적 변수 기반의 비용 함수 활용.
-
로봇 설계 파일 활용:
- URDF 등 로봇 설계 파일에서 제약 조건의 기본값(관절 각도, 속도, 토크 등)을 자동으로 가져옴.
-
학습 과정에서의 제약 조건 처리:
- 제약이 만족되면 비용 함수는 0에 가깝고, 위반 시 패널티가 적용됨.
- 이미 만족된 제약은 정책 최적화에 영향을 미치지 않음 (로그 배리어 함수의 특성).
