7. 시계열의 상태공간 모델
- 선형 가우스 모델에 적용된 칼만 필터
- 은닉 마르코프 모형
- 베이즈 구조적 시계열
관측에 기반한 근본 상태를 추정하는 작업
- 필터링 : 상태에 대한 추정의 갱신에 가장 최근 정보에 가중치를 주는 방법
- 예측 : 미래에 대한 어떠한 정보도 없이 미래 상태를 예측
- 평활화 : 미래와 과거 정보 모두 사용해서 특정 시간에서의 상태를 가장 잘 추정
상태공간 모델의 장단점
장점
- 노이즈가 낀 데이터 자체보다 시계열에서 가장 흥미로운 노이즈한 데이터의 생성 과정과 상태를 모델링할 수 있게 해줌
- 시간에 따른 상관계수 및 파라미터의 변화를 허용
단점
- 상태공간 모델이 너무 유연해 수많은 파라미터의 설정이 가능하다보니 모든 속성이 심도있게 연구되지 않음
- 수많은 파라미터로 구성된 모델은 계산적으로 부담이 되고 과적합에 취약함
칼만 필터
: 시계열로부터 새로운 정보를 결합하는 데 사용되고 과거에 알려진 내부 상태 추정 정보를 지능적으로 결합해줌
→ 계산이 비교적 간단하고 미래 예측이나 현재를 추정하는 데 과거 데이터의 저장이 필요없다
상태 및 관측이 다음과 같은 역동성을 가진다고 상정하는 선형 가우스 모델
시간 에서의 상태는 이전 시간 단계의 상태 항, 외부압력에 대한 항, 확률적 항에 대한 함수로 표현할 수 있다
칼만 필터에 적용 가능한 기본 공식 → 시간 에서 새로운 정보가 주어졌을 때 추정을 갱신하는 방법
:
위 식은 만 관측 가능하며 정확한 상태는 모른 채 상태를 추론했다는 상황을 상정
: 공분산 추정 → 시간 에서의 측정이 고려되기 전의 추정
: 측정 오차의 분산
모델의 동작 방식 : 시간 0에서 시간 뒤로 움직이며 예측과 갱신을 반복
- 예측
- 필터링
코드로 표현한 칼만필터
오차가 쉽게 발생하는 센서를 사용하여 뉴턴 역학을 따르는 물체를 추적하는 예
물체의 위치를 물체의 속도와 가속도에 대한 함수로 보는 뉴턴 운동 법칙에 따라 시계열 생성
## 로켓은 시간 단계를 100번 거침
ts_length = 100
## 가속도가 움직임을 주도
import numpy as np
aa = np.array([0.5])
a = np.repeat(aa, ts_length)
## 위치와 속도는 0에서 시작
zero = np.array([0])
x = np.repeat(zero, ts_length)
v = np.repeat(zero, ts_length)
for i in range(2, ts_length):
x[i] = v[i-1]*2+x[i-1]+(1/2)*(a[i-1]**2)
x[i] = x[i]+np.random.normal(0, 20, 1)
v[i] = v[i-1]+2*a[i-1]로켓의 위치, 속도, 가속도에 대한 그래프를 그려보면 다음과 같다

→ 선형적으로 증가하는 속도에 영향을 주는 일정한 가속도가 위로 솟구치는 볼록 모양의 그래프를 만들어낸다
측정된 값이 실제 위치와 어떤 관계를 갖는가
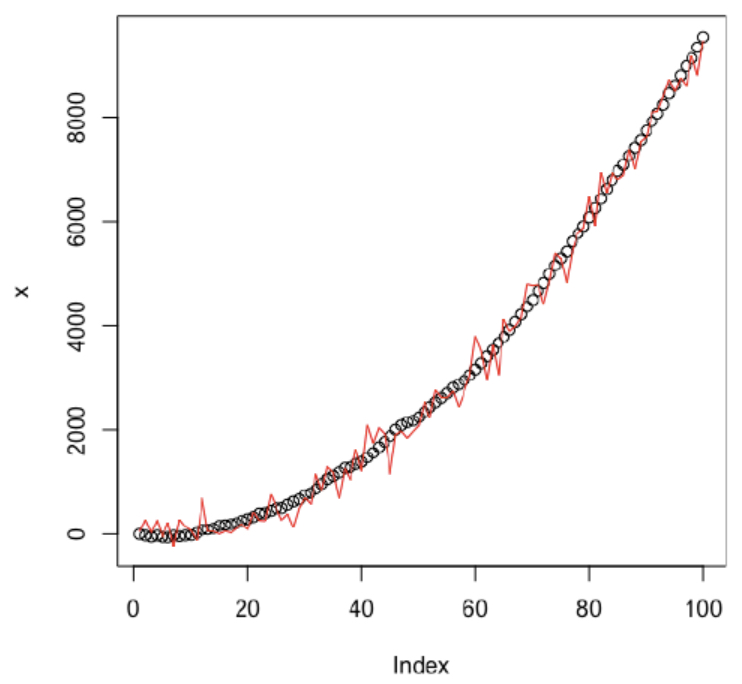
칼만 필터 적용
def Kalman(z, Q, R, A, H):
dimState = Q.shape[1]
xhatminus = np.reshape(np.repear(zero, ts_length*dimState), (ts_length, dimState))
xhat = np.reshape(np.repeat(zero, ts_length*dimState), (ts_length, dimState))
Pminus = np.reshape(np.repeat(zero, ts_length*dimState*dimState), (ts_length, dimState, dimState))
P = np.reshape(np.repeat(zero, ts_length*dimState*dimState), (ts_length, dimState, dimState))
K = np.reshape(np.repeat(zero, ts_length*dimState), (ts_length, dimState))
## 초기 추측 - 모든 지표는 0으로 시작한다
xhat[1,:] = np.repeat(zero, dimState)
P[1,:,:] = np.diag(dimState)
## 시간 갱신
for k in range(2, ts_length):
## 예측
xhatminus[k,:] = A@(np.matrix(xhat[k-1,:]))
Pminus[k,:,:] = A@P[k-1,:,:]@np.transpose(A) + Q
##필터링
K[k,:] = Pminus[k,:,:]@H@np.linalg.inv(H.T@Pminus[k,:,:]@H+R)
xhat[k,:]=xhatminus[k,:]+K[k,:]@(z[k]-H.T@xhatminus[k,:])
P[k,:,:] = (np.diag(dimState)-K[k,:]@H.T)@Pminus[k,:,:]
##예측과 평활화된 값 모두 반환
return list(xhat, xhatminus)칼만 필터는 측정 오차에서 많은 노이즈를 제거 → 제거하는 정도는 측정 오차의 파라미터 R 값에 따라 달라짐
칼만 필터의 이점 : 재귀성 - 과정이 반복될 때마다 모든 데이터를 살펴볼 필요 없다
요약 통계를 사용해 지능적인 방식으로 갱신을 수행한다는 점이 칼만 필터의 장점
은닉 마르코프 모형
: 시계열 모델링에 유용하며 관측 가능 변수가 시스템을 가장 잘 묘사하지는 못한다는 개념에서 영감을 받음
: 은닉 마르코프 모형에서 상정하는 과정은 이산적 상태들 간의 이동으로 묘사될 수 있는 비선형성
HMM은 직접적으로 관측이 불가능한 상태를 가진 시스템을 상정 → 미래 사건 '기억 없음'
마르코프 과정 : 행렬로 묘사
ex) 상태 A와 B 사이에서 출렁이는 시스템
두 상태 모두 다른 시간 단계에서 통계적으로 다른 상태로 바뀌는 것보다 현 상태를 유지할 가능성이 높음
→현재 시스템의 상태가 A일 때 상태 A를 유지할 확률은 0.7이고, 상태 B로 바뀔 확률은 0.3
은닉 마르코프 모형은 관측으로부터 시스템의 상태를 직접적으로 추론할 수 없다는 것을 제외하고는 마르코프 모형과 같은 종류의 시스템을 표현

이 데이터에 HMM을 적용한다고 할 때, 시각적인 정보만으로는 상태가 몇 개 존재하는지, 무엇이 각 상태를 구분짓는지, 시스템의 상태 간 전환시점은 어디인지 파악하기 어렵다
모델을 적합시키는 방법
은닉 상태들의 선험적 지식 없이 은닉 상태를 식별하는 방법 : 반복성
HMM 과정의 묘사와 적합에는 다음의 변수가 필요함
- 시스템을 구성하는 개별 상태 :
- 모든 시간 단계에서 상태 에서 로 바뀌는 전환에 대한 전환 확률 행렬 :
- 관측된 시계열 과정에서 샘플링된 관측의 정렬된 순서 :
- 상태 일 때 관측될 값 의 방출 확률 :
- 시스템 시작 시 갖는 상태에 대한 초기 확률 분포 :
📌바움-웰치 알고리즘
: 모든 파라미터 값을 추정하는 복잡한 작업의 가이드 역할을 하는 알고리즘
- 각 은닉상태 간의 전환 확률을 식별할 때
- 전체 관측에서 각 시간 단계별 가장 가능성이 높은 은닉 상태를 식별할 때
1 우도함수를 정의
우도함수 : 주어진 가설 파라미터의 순서에 대한 관측의 확률
→ 주어진 방출 확률의 파라미터에 대한 관측 순서의 우도를 묘사
시간 단계가 많아질수록 복잡도가 지수적으로 증가하므로 격자탐색이 현실적이지 못하는 등의 어려움 존재
→ EM 알고리즘 적용
1. 두 개의 분포를 상정하는 무작위 사건 및 각 시간 단계에서 특정 상태일 확률을 결정
2. 각 시간 단계에 추정상 상태를 할당하면, 그 추정 상태로 방출 확률을 재추정함
3. 이 과정을 반복하여 궤적의 추적 향상을 위해 새롭게 갱신된 방출 확률변수 사용
📌비터비 알고리즘
: 특정 해결책에 도달하기 위해 부분적인 해결책을 만들고 저장해 적합 범위를 안전하면서도 효율적으로 탐색하게끔 설게된 것
→ 동적 프로그래밍 알고리즘
HMM의 적합 과정
HMM은 다양한 종류의 데이터를 분석하는 데 적합하며 단순한 포인트 추정이나 예측 이상을 제공
HMM을 사용할 때 직면할 수 있는 몇 가지 추론 작업
- 관측의 계열을 생성하는 상태들의 가장 가능성 있는 설명을 결정
- 관측의 계열, 상태에 대한 설명, 각 상태의 방출과 전환 확률을 통해 가장 가능성이 높은 상태의 연속적인 순서를 결정
- 필터링과 평활화
베이즈 구조적 시계열 (BSTS)
: 시스템에 대해 이미 알려진 사실이나 흥미로운 가설을 반영하는 복잡한 모델을 구축하기 위해 이미 존재하는 요소를 활용하는 방법을 제공
BSTS 모델의 적합
- 사전 확률의 세부 사항을 포함한 구조적 모델을 정의
- 관측된 데이터로 상태의 추정을 갱신하는 데 칼만 필터를 적용
- 스파이크앤슬랩 방법을 사용해 구조적 모델 내의 변수 선택을 수행
- 예측의 생성을 위한 결과의 결합에 베이즈 모델 평균화를 적용
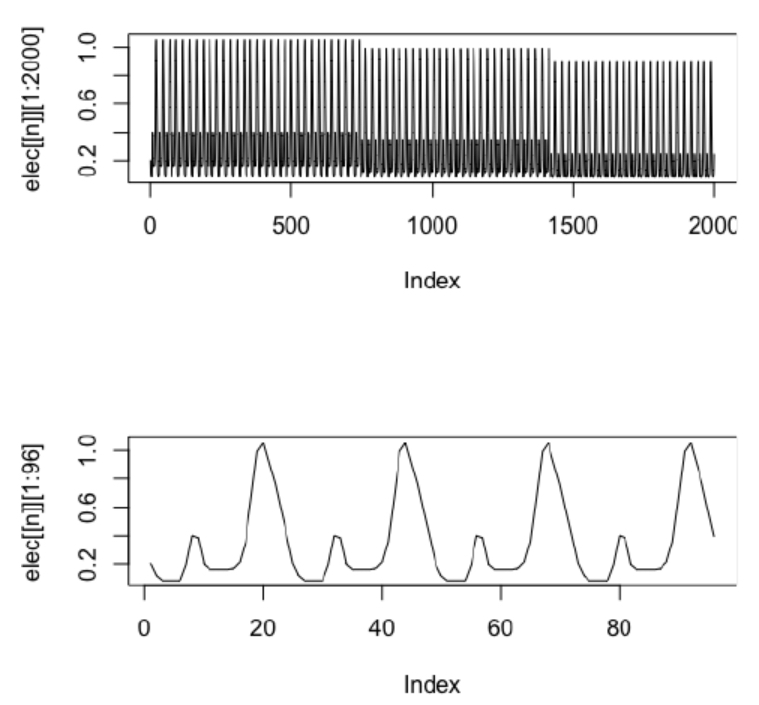
위의 그래프는 모델을 적합시켜야 하는 전체 계열, 하단 그래프는 전체를 짧게 잘라낸 부분집합이다
이렇게 데이터를 보면 어떤 식으로 모델을 만들지 감을 얻을 수 있다
bsts 패키지의 장점
: 사후 확률에 대한 마르코프체인 몬테카를(MCMC)로 계산을 여러 번 수행할 수 있다
: 계절성 요소도 검사할 수 있다
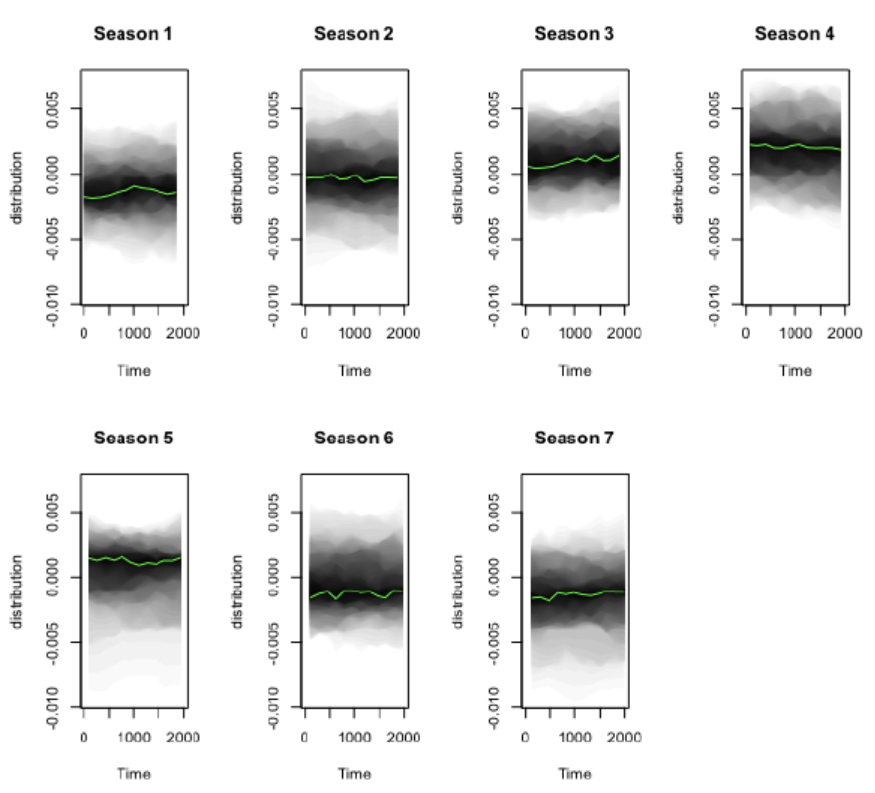
→ 요일별 계절성은 서로 다른 요일에 따라 차이가 있다는 것을 보여줌
미래 예측에 대한 사후 분포의 전체 그래프
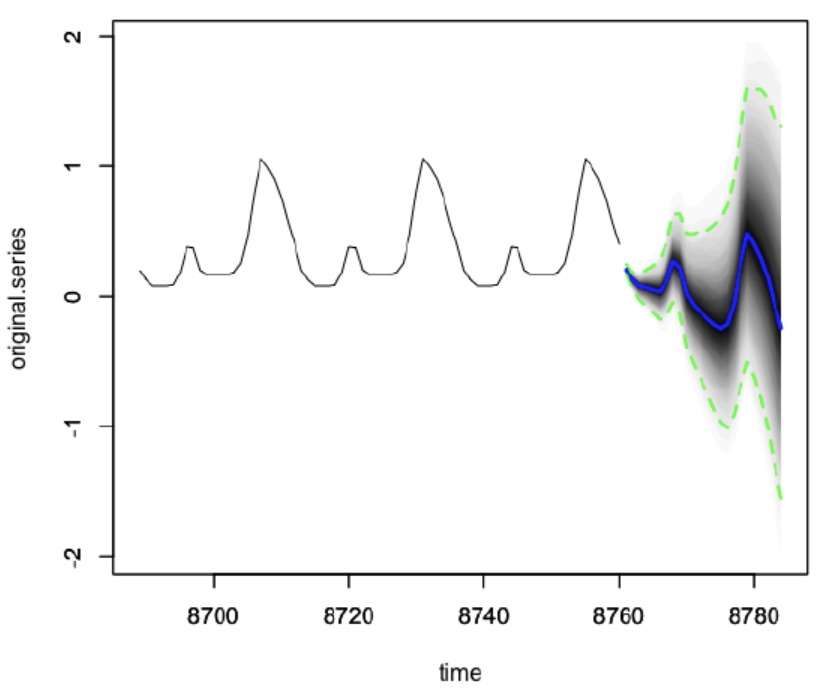
→ 마지막 72시간의 데이터와 예측된 24시간의 데이터의 결합
→ 미래를 예측할수록 예측의 분포가 넓게 퍼짐
bsts 패키지의 유용한 옵션
- 비표준적인 사전 확률을 지정할 수 있다
- 회귀 모델 선택에 스파이크앤슬랩 방법을 사용할 수 있다
- 베이즈 모델 평균화를 사용할 수 있다
