JS - 자료 구조

배열 와 리스트
배열
기본적으로 자료구조에서 말하는 배열과 자바스크립트의 배열은 조금 다릅니다. 일단 우리는 JS 신을 믿기 때문에 JS 기반으로 설명하겠습니다.
JavaScript에서 배열의 특징은 다음과 같습니다.
-
배열은 요소 모음을 저장하는 데 사용되는 데이터 구조입니다.
-
배열의 요소는 숫자, 문자열 및 객체를 포함한 모든 데이터 유형일 수 있습니다.
-
배열의 각 요소는 0부터 시작하는 인덱스로 식별됩니다.
-
배열은 변경 가능합니다. 즉, 배열에서 요소를 추가하거나 제거할 수 있습니다.
-
배열의 길이는 요소를 추가하거나 제거할 때 동적으로 변경될 수 있습니다.
-
인덱스를 사용하여 배열 요소에 액세스할 수 있으며 for 루프를 사용하여 배열 요소를 반복할 수 있습니다.
-
JavaScript의 배열은 다차원적일 수 있습니다. 즉, 배열 안에 배열이 있을 수 있습니다.
-
JavaScript 배열에는 배열 요소에 대해 다양한 작업을 수행할 수 있는 내장 메서드가 있습니다.
-
JavaScript의 배열은 참조 유형입니다. 즉, 배열을 변수에 할당할 때 실제로는 배열의 복사본이 아니라 배열에 대한 참조를 할당하는 것입니다.
-
배열은 스택, 대기열 및 트리와 같은 데이터 구조를 나타내는 데 사용할 수 있으며 컴퓨터 과학 및 프로그래밍의 기본 데이터 구조입니다.
리스트
단일 연결 리스트
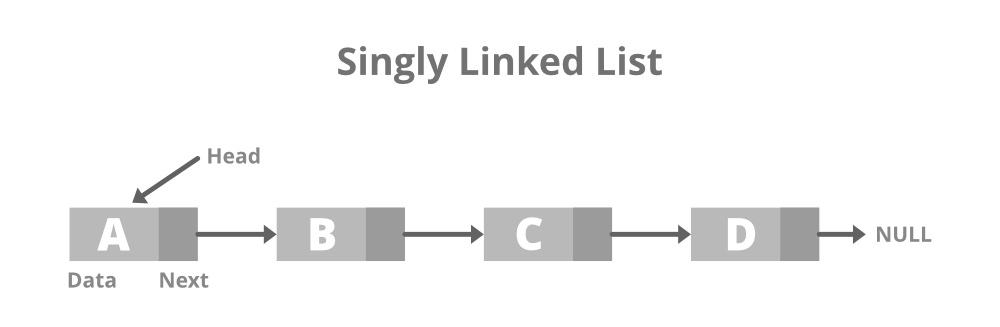
단일 연결 목록에서 각 노드는 시퀀스의 다음 노드에 대한 참조를 갖지만 이전 노드에 대한 참조는 갖지 않습니다. 즉, 목록 순회는 머리(첫 번째 요소)에서 꼬리(마지막 요소)까지 한 방향으로만 수행될 수 있습니다. 단일 연결 목록에서 요소를 삽입하고 삭제하려면 인접한 노드의 링크를 수정해야 합니다.
장점:
- 목록 중간에 요소를 삽입하고 삭제하는 데 효율적입니다.
- 노드당 하나의 참조만 필요하므로 이중 연결 목록에 비해 적은 메모리가 사용됩니다.
단점:
- 단일 연결 목록의 요소에 액세스하는 것은 요소가 헤드 노드에서 시작하여 순차적으로 순회해야 하므로 배열보다 덜 효율적입니다.
- 목록 끝에 있는 요소에 액세스하는 데 효율적이지 않습니다.
class Node {
constructor(data, next = null) {
this.data = data;
this.next = next;
}
}
class SinglyLinkedList {
constructor() {
this.head = null;
this.tail = null;
this.length = 0;
}
append(data) {
const node = new Node(data);
if (!this.head) {
this.head = node;
this.tail = node;
} else {
this.tail.next = node;
this.tail = node;
}
this.length++;
}
delete(data) {
if (!this.head) {
return;
}
if (this.head.data === data) {
this.head = this.head.next;
this.length--;
return;
}
let current = this.head;
while (current.next) {
if (current.next.data === data) {
current.next = current.next.next;
if (current.next === null) {
this.tail = current;
}
this.length--;
break;
}
current = current.next;
}
}
}이중 연결 리스트
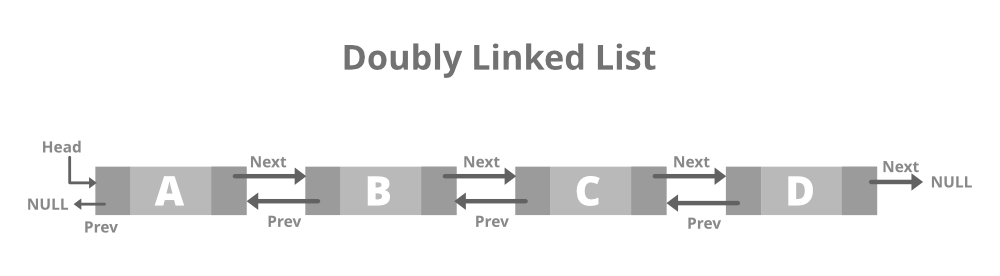
이중 연결 목록에서 각 노드는 시퀀스의 다음 노드와 이전 노드 모두에 대한 참조를 갖습니다. 이렇게 하면 양방향으로 목록을 순회할 수 있으므로 특정 작업에 유용할 수 있습니다. 이중 연결 목록에서 요소를 삽입하고 삭제하려면 인접한 노드의 링크도 수정해야 하지만 이 경우 한 개가 아닌 두 개의 링크 집합을 업데이트해야 합니다.
장점:
- 목록 중간에 요소를 삽입 및 삭제하고 어느 방향으로든 요소에 액세스하는 데 효율적입니다.
- 목록 반전과 같은 특정 작업에서 더 많은 유연성을 허용합니다.
단점:
- 각 노드가 하나가 아닌 두 개의 참조를 가지므로 단일 연결 목록에 비해 더 많은 메모리가 필요합니다.
class Node {
constructor(data, prev = null, next = null) {
this.data = data;
this.prev = prev;
this.next = next;
}
}
class DoublyLinkedList {
constructor() {
this.head = null;
this.tail = null;
this.length = 0;
}
append(data) {
const node = new Node(data, this.tail);
if (!this.head) {
this.head = node;
this.tail = node;
} else {
this.tail.next = node;
this.tail = node;
}
this.length++;
}
delete(data) {
if (!this.head) {
return;
}
let current = this.head;
while (current) {
if (current.data === data) {
if (current === this.head) {
this.head = current.next;
if (this.head) {
this.head.prev = null;
}
} else if (current === this.tail) {
this.tail = current.prev;
if (this.tail) {
this.tail.next = null;
}
} else {
current.prev.next = current.next;
current.next.prev = current.prev;
}
this.length--;
break;
}
current = current.next;
}
}
}배열 vs 리스트
list:
- 동적으로 확장 및 축소 가능
- 목록 중간에 효율적인 삽입 및 삭제 허용
- 요소가 연속 메모리에 저장되지 않기 때문에 요소에 액세스하는 것이 배열보다 느림
- 노드마다 크기와 구조가 다를 수 있음
- 노드 포인터로 인해 배열보다 더 많은 메모리 오버헤드가 필요할 수 있음
array(자료구조 관점):
- 고정 크기
- 요소의 효율적인 임의 액세스 허용
- 중간에 요소를 추가하거나 제거하면 이동 또는 채우기로 인해 속도가 느려질 수 있습니다.
- 모든 요소는 크기와 유형이 동일해야 합니다.
- 경우에 따라 연결된 목록보다 메모리 효율적일 수 있음
전반적으로 연결된 목록은 빈번한 삽입 또는 삭제가 필요한 상황에 더 적합한 반면 배열은 임의 액세스 및 계산이 중요한 상황에 더 적합합니다. 연결 목록과 배열 사이의 선택은 응용 프로그램의 특정 요구 사항에 따라 다릅니다.
코딩테스트에서의 의미
- 배열 혹은 스택의 기능이 필요할 때 사용할 수 있다.
- 내부적으로 포인터를 사용하기 때문에, 연결 리스트의 장점도 가지고 있다.
- 그러나 큐의 기능이 필요할 때는 직접 구현해야한다.
스택
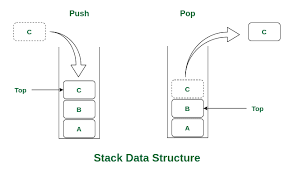
스택 데이터 구조는 푸시 및 팝의 두 가지 주요 작업을 지원하는 요소 모음입니다. 푸시 작업은 스택 맨 위에 요소를 추가하고 팝 작업은 스택에서 맨 위 요소를 제거합니다.
- LIFO(Last In, First Out) 순서: 스택에 마지막으로 푸시된 요소가 가장 먼저 팝 오프됩니다.
- 동적 크기: 스택은 요소가 푸시되거나 팝될 때 동적으로 확장되거나 축소될 수 있습니다.
- 제한된 액세스: 스택의 맨 위 요소만 액세스하거나 제거할 수 있습니다.
- 작업: 스택에서 지원하는 주요 작업은 푸시 및 팝이지만 일부 스택은 peek(최상위 요소를 제거하지 않고 반환), clear(스택에서 모든 요소 제거) 또는 크기(원소를 반환)와 같은 다른 작업도 지원할 수 있습니다. 스택의 요소 수).
- 구현: 스택은 배열 또는 연결 목록을 사용하여 구현할 수 있습니다.
코드로 구현하기
class Stack {
constructor() {
this.items = [];
}
push(element) {
this.items.push(element);
}
pop() {
if (this.isEmpty()) {
return "Underflow";
}
return this.items.pop();
}
peek() {
return this.items[this.items.length - 1];
}
isEmpty() {
return this.items.length == 0;
}
printStack() {
let str = "";
for (let i = 0; i < this.items.length; i++) {
str += this.items[i] + " ";
}
return str;
}
}
- constructor: items 배열을 초기화합니다.
- push: 스택의 맨 위에 요소를 추가합니다.
- pop: 스택에서 최상위 요소를 제거하고 반환합니다. 스택이 비어 있으면 "언더플로" 메시지를 반환합니다.
- peek: 스택의 맨 위 요소를 제거하지 않고 반환합니다.
- isEmpty: 스택이 비어 있으면 true를 반환하고 그렇지 않으면 false를 반환합니다.
- printStack: 스택 요소의 문자열 표현을 반환합니다.
아래는 위의 코드를 사용했을 때의 예시 코드 입니다 .
let stack = new Stack();
stack.push(10);
stack.push(20);
stack.push(30);
console.log(stack.printStack()); // Output: 10 20 30
console.log(stack.peek()); // Output: 30
stack.pop();
console.log(stack.printStack()); // Output: 10 20큐
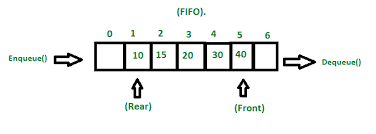
큐 데이터 구조는 요소 모음을 저장하는 또 다른 기본 데이터 구조입니다. 스택과 비슷하지만 동작이 다릅니다. 대기열은 대기열에 넣기와 대기열에서 빼기라는 두 가지 주요 작업을 지원합니다. enqueue 작업은 요소를 대기열 끝에 추가하는 반면 dequeue 작업은 요소를 제거하고 대기열 맨 앞에 반환합니다.
- FIFO(First In, First Out) 순서: 대기열에 추가된 첫 번째 요소가 제거되는 첫 번째 요소입니다.
- 동적 크기: 대기열은 요소가 추가되거나 제거됨에 따라 동적으로 확장되거나 축소될 수 있습니다.
제한된 액세스: 큐의 앞에 있는 요소만 제거할 수 있고 큐의 뒤에 있는 요소만 액세스할 수 있습니다. - 작업: 대기열에서 지원하는 주요 작업은 대기열에 넣기 및 대기열에서 빼기이지만 일부 대기열은 엿보기(앞쪽 요소를 제거하지 않고 반환), 지우기(대기열에서 모든 요소 제거) 또는 크기(대기열에서 모든 요소 반환)와 같은 다른 작업도 지원할 수 있습니다. 대기열의 요소 수).
- 구현: 대기열은 배열 또는 연결 목록을 사용하여 구현할 수 있습니다.
class Queue {
constructor() {
this.items = [];
}
enqueue(element) {
this.items.push(element);
}
dequeue() {
if (this.isEmpty()) {
return "Underflow";
}
return this.items.shift();
}
front() {
if (this.isEmpty()) {
return "No elements in Queue";
}
return this.items[0];
}
isEmpty() {
return this.items.length == 0;
}
printQueue() {
let str = "";
for (let i = 0; i < this.items.length; i++) {
str += this.items[i] + " ";
}
return str;
}
}- constructor: items 배열을 초기화합니다.
- enqueue: 큐의 끝에 요소를 추가합니다.
- dequeue: 큐에서 앞쪽 요소를 제거하고 반환합니다. 대기열이 비어 있으면 "언더플로" 메시지를 반환합니다.
- front: 큐의 앞 요소를 제거하지 않고 반환합니다.
- isEmpty: 큐가 비어 있으면 true를 반환하고 그렇지 않으면 false를 반환합니다.
- printQueue: 대기열 요소의 문자열 표현을 반환합니다.
아래는 큐 자료구조를 사용하는 예시 코드입니다.
let queue = new Queue();
queue.enqueue(10);
queue.enqueue(20);
queue.enqueue(30);
console.log(queue.printQueue()); // Output: 10 20 30
console.log(queue.front()); // Output: 10
queue.dequeue();
console.log(queue.printQueue()); // Output: 20 30트리
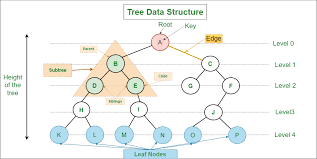
트리 데이터 구조는 엣지(edge)로 연결된 노드로 구성된 널리 사용되는 계층적 데이터 구조입니다. 트리의 각 노드는 상위 노드가 없는 루트 노드를 제외하고 0개 이상의 하위 노드를 가질 수 있습니다.
- 루트: 트리의 최상위 노드를 루트 노드라고 합니다.
- 부모: 자식 노드가 있는 노드를 부모 노드라고 합니다.
- 자식: 부모 노드가 있는 노드를 자식 노드라고 합니다.
- 리프: 자식이 없는 노드를 리프 노드라고 합니다.
- 하위 트리: 하위 트리는 노드와 모든 자손으로 구성된 트리입니다.
- 높이: 트리의 높이는 루트 노드에서 리프 노드까지 가장 긴 경로의 길이입니다.
- 깊이: 노드의 깊이는 루트 노드에서 해당 노드까지의 경로 길이입니다.
- 이진 트리: 이진 트리는 각 노드에 최대 두 개의 자식이 있는 트리입니다.
이진 트리의 코드
class TreeNode {
constructor(value) {
this.value = value;
this.left = null;
this.right = null;
}
}
class BinaryTree {
constructor() {
this.root = null;
}
insert(value) {
const newNode = new TreeNode(value);
if (this.root === null) {
this.root = newNode;
} else {
this._insertNode(this.root, newNode);
}
}
_insertNode(node, newNode) {
if (newNode.value < node.value) {
if (node.left === null) {
node.left = newNode;
} else {
this._insertNode(node.left, newNode);
}
} else {
if (node.right === null) {
node.right = newNode;
} else {
this._insertNode(node.right, newNode);
}
}
}
search(value) {
return this._searchNode(this.root, value);
}
_searchNode(node, value) {
if (node === null) {
return null;
} else if (value < node.value) {
return this._searchNode(node.left, value);
} else if (value > node.value) {
return this._searchNode(node.right, value);
} else {
return node;
}
}
traverseInOrder() {
const result = [];
this._traverseInOrder(this.root, result);
return result;
}
_traverseInOrder(node, result) {
if (node !== null) {
this._traverseInOrder(node.left, result);
result.push(node.value);
this._traverseInOrder(node.right, result);
}
}
}
// Example usage
const tree = new BinaryTree();
tree.insert(5);
tree.insert(3);
tree.insert(7);
tree.insert(1);
tree.insert(4);
tree.insert(6);
tree.insert(8);
console.log(tree.traverseInOrder()); // [1, 3, 4, 5, 6, 7, 8]
console.log(tree.search(4)); // TreeNode { value: 4, left: TreeNode {...}, right: TreeNode {...} }
우선 순위 큐
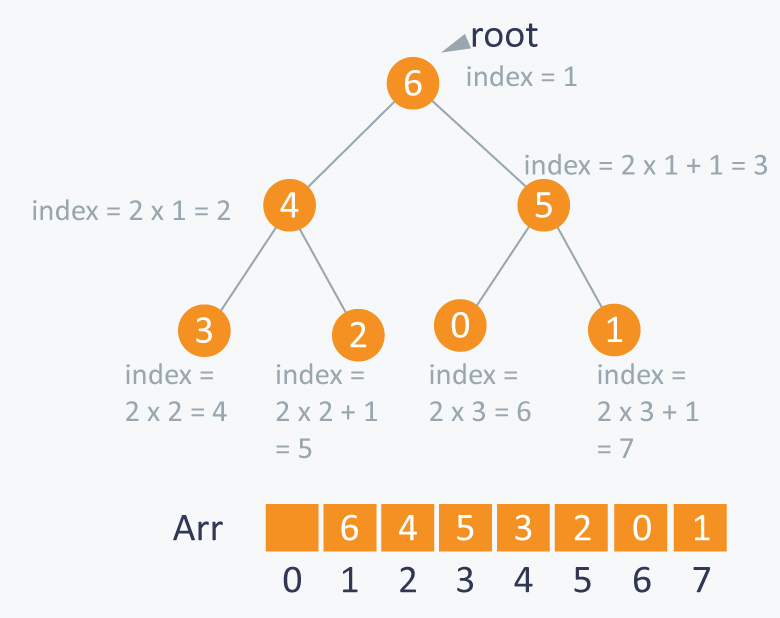
우선순위 큐는 각 요소가 우선순위 값과 연관되는 특별한 유형의 큐입니다. 우선순위 대기열에 있는 요소의 우선순위에 따라 처리되는 순서가 결정됩니다. 우선 순위 값이 높은 요소는 우선 순위 값이 낮은 요소보다 먼저 처리됩니다
즉, 우선순위 대기열은 일반 대기열과 유사하지만 대기열의 각 항목에는 우선순위가 연결되어 있다는 점만 다릅니다. 항목이 우선순위 대기열에 추가되면 항목이 추가된 순서가 아니라 우선순위에 따라 대기열에 배치됩니다.
우선 순위 큐는 힙, 이진 검색 트리 및 배열을 비롯한 다양한 데이터 구조를 사용하여 구현할 수 있습니다. 가장 일반적인 구현은 힙 데이터 구조를 사용합니다.
우선 순위 대기열은 일반적으로 운영 체제, 네트워크 라우팅 알고리즘 및 시뮬레이션 시스템과 같은 컴퓨터 과학 응용 프로그램에서 사용됩니다.
힙 (heap)
- 힙은 각 노드의 값이 하위 노드의 값보다 크거나 같거나(최대 힙의 경우) 작거나 같은(최소 힙의 경우) 완전 이진 트리 기반 데이터 구조입니다.
- 최대 힙에서 각 노드의 값은 하위 노드의 값보다 크거나 같습니다. 루트 노드는 힙에서 가장 큰 값을 포함합니다.
- 최소 힙에서 각 노드의 값은 하위 노드의 값보다 작거나 같습니다. 루트 노드는 힙에서 가장 작은 값을 포함합니다.
- 힙의 성능은 Big O 표기법을 사용하여 표시되는 시간 복잡성으로 측정됩니다. 힙에서 삽입, 삭제 및 검색 작업의 시간 복잡도는 O(log n)이며 여기서 n은 힙의 노드 수입니다.
최소 힙 구조에서 새로운 값이 삽입 된다면?
- 최소 힙 구조에 새 값이 삽입되면 힙의 맨 아래 수준에서 다음으로 사용 가능한 위치(맨 아래 수준에서 사용 가능한 가장 왼쪽 위치)에 배치됩니다.
- 그런 다음 상위 노드와 비교됩니다. 부모 노드의 값이 삽입된 노드의 값보다 크면 교체됩니다.
- 이 과정은 부모 노드가 삽입된 노드보다 작거나 삽입된 노드가 루트 노드에 도달할 때까지 반복됩니다.
- 삽입된 노드가 적절한 위치에 있으면 최소 힙 속성이 복원됩니다.
자바스크립트 코드
직접 짜는 것...그것은 거의 무리...
class MaxHeap {
constructor() {
this.heap = [];
}
getLeftChildIndex(parentIndex) {
return (2 * parentIndex) + 1;
}
getRightChildIndex(parentIndex) {
return (2 * parentIndex) + 2;
}
getParentIndex(childIndex) {
return Math.floor((childIndex - 1) / 2);
}
hasLeftChild(index) {
return this.getLeftChildIndex(index) < this.heap.length;
}
hasRightChild(index) {
return this.getRightChildIndex(index) < this.heap.length;
}
hasParent(index) {
return this.getParentIndex(index) >= 0;
}
leftChild(index) {
return this.heap[this.getLeftChildIndex(index)];
}
rightChild(index) {
return this.heap[this.getRightChildIndex(index)];
}
parent(index) {
return this.heap[this.getParentIndex(index)];
}
swap(indexOne, indexTwo) {
const temp = this.heap[indexOne];
this.heap[indexOne] = this.heap[indexTwo];
this.heap[indexTwo] = temp;
}
peek() {
if (this.heap.length === 0) {
return null;
}
return this.heap[0];
}
insert(value) {
this.heap.push(value);
this.heapifyUp();
}
heapifyUp() {
let index = this.heap.length - 1;
while (this.hasParent(index) && this.parent(index) < this.heap[index]) {
const parentIndex = this.getParentIndex(index);
this.swap(index, parentIndex);
index = parentIndex;
}
}
poll() {
if (this.heap.length === 0) {
return null;
}
const item = this.heap[0];
this.heap[0] = this.heap.pop();
this.heapifyDown();
return item;
}
heapifyDown() {
let index = 0;
while (this.hasLeftChild(index)) {
let largerChildIndex = this.getLeftChildIndex(index);
if (this.hasRightChild(index) && this.rightChild(index) > this.leftChild(index)) {
largerChildIndex = this.getRightChildIndex(index);
}
if (this.heap[index] > this.heap[largerChildIndex]) {
break;
} else {
this.swap(index, largerChildIndex);
}
index = largerChildIndex;
}
}
}
그래프
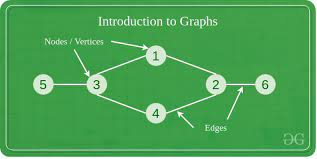
그래프는 vertices 집합과 이를 연결하는 edges 집합으로 구성된 데이터 구조입니다. vertices 간의 관계는 인접 행렬 또는 인접 목록을 사용하여 나타낼 수 있습니다. 인접 행렬은 두 vertices 사이에 edges가 있는지 여부를 저장하는 2차원 배열이며, 인접 목록은 각 vertices의 이웃을 저장하는 연결 목록 모음입니다.
-
vertice: 정점(또는 노드)은 그래프의 기본 단위입니다. 일반적으로 그래프 다이어그램에서 점이나 원으로 표시됩니다.
-
edge: 에지는 두 정점을 연결하는 선으로 이들 간의 관계를 나타냅니다. 에지에는 관련 가중치 또는 비용이 있을 수 있습니다.
-
인접행렬(Adjacency Matrix): 인접행렬은 그래프에서 두 정점 사이에 간선이 있는지 여부를 저장하는 2차원 배열이다.
-
인접 리스트: 인접 리스트는 그래프에서 각 정점의 이웃을 저장하는 연결 리스트의 모음입니다.
인접 행렬
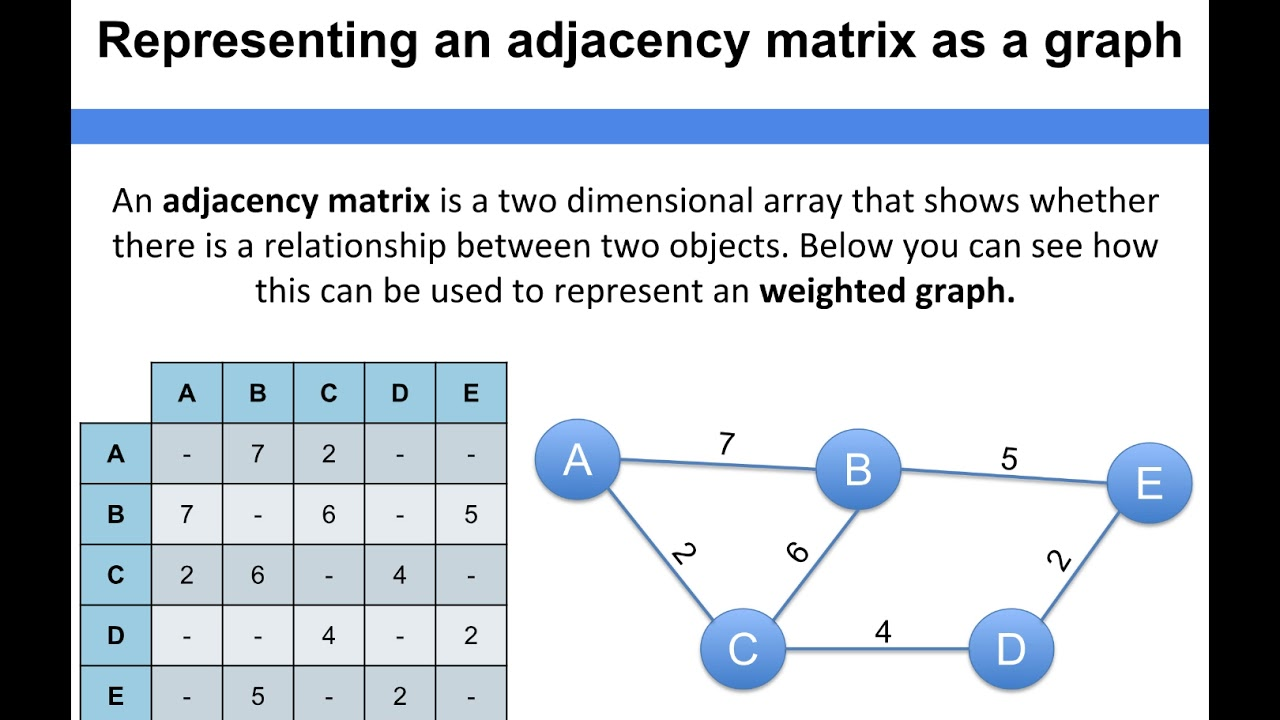
정점에 해당하는 행과 열이 있는 행렬과 정점 사이의 가장자리를 나타내는 셀로 나타낼 수 있습니다. 값이 1인 셀은 가장자리가 있음을 나타내고 값이 0인 셀은 가장자리가 없음을 나타냅니다. 유향 그래프의 경우 행렬이 대칭이 아닐 수 있습니다.
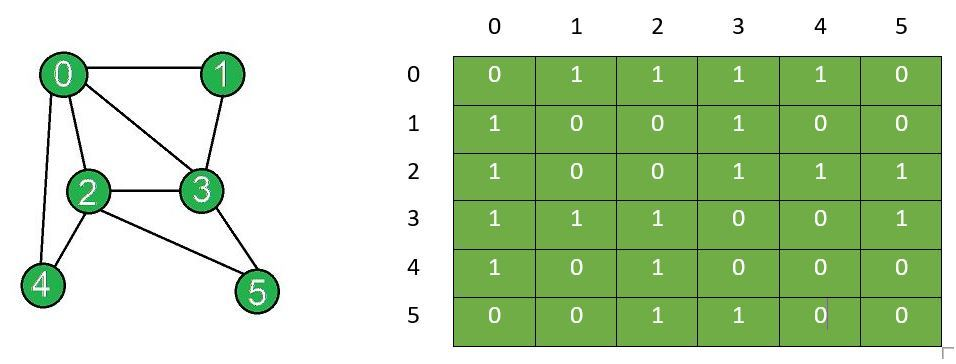
추가로. 무방향 무가중치 그래프가 있습니다.
연결되어 있는 상태만 나타내는 방식입니다.
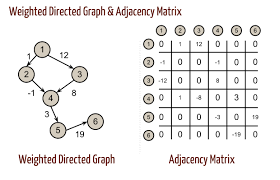
아래는 방향 + 가중치 그래프 입니다. 나머지는 응용해서 생각해보세요
인접 리스트
각 꼭짓점에는 목록에 인덱싱하여 액세스할 수 있는 이웃 목록이 연결되어 있습니다. 연결된 목록의 각 항목은 정점을 이웃에 연결하는 가장자리를 나타내며 가장자리의 가중치와 같은 정보를 포함할 수 있습니다.