최장증가수열

무작위 수가 나열되어있는 수열에서 특정 수들을 뽑아 순서를 바꾸지 않고 나열하여 새로운 수열을 만들었을때 해당 수열이 오름차순이면서 길이가 최대인 경우의 수열 크기를 찾는 알고리즘이다.
예를들어 [3 8 10 9 5 14 2 18 20 1 9] 라는 수열이 있을경우 [3 8 10 14 18 20]보다 긴 증가 수열이 없으므로 최장 증가 수열이고 크기는 6이다. 구현하는 방법은 두 가지가 있다.

방법(1)

첫번째 방법은 DP를 사용하여 구현한다. DP에 저장되는 값은 DP[i] = i 번째 수를 마지막으로 하는 최장 증가 수열 크기 이다. 처음에 주어지는 수열의 배열이름을 Num[] 이라고 하자.
점화식은 DP[i - 1] 부터 DP[0]까지 탐색하며 Num[k] < Num[i] (0 <= k <= i - 1)이라면 i 번째 수가 추가되어도 증가하는 수열이므로 DP[i] = max (DP[i], DP[k] + 1) 이다. 따라서 최장 증가 수열의 크기는 DP배열의 최댓값이다.

Num[k] >= Num[i] 이라면 i번째 수가 감소하기 때문에 계산하지 않고 넘어간다. 유의할 점은 숫자 한개만 있는경우도 증가수열로 치기 때문에 DP[i]의 최소값은 항상 1이다.

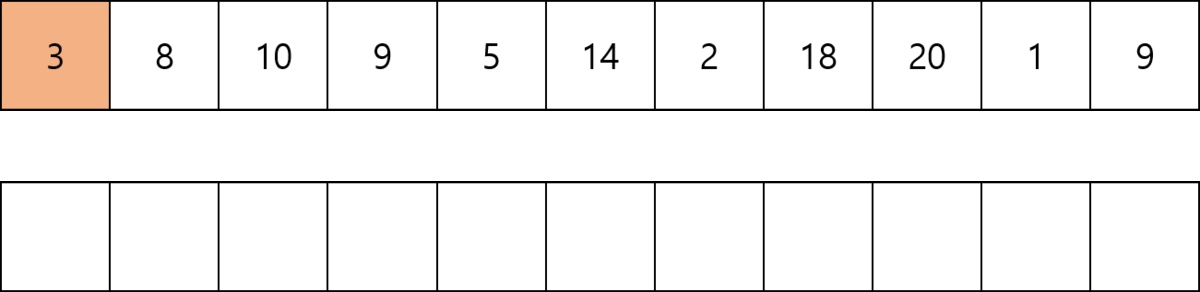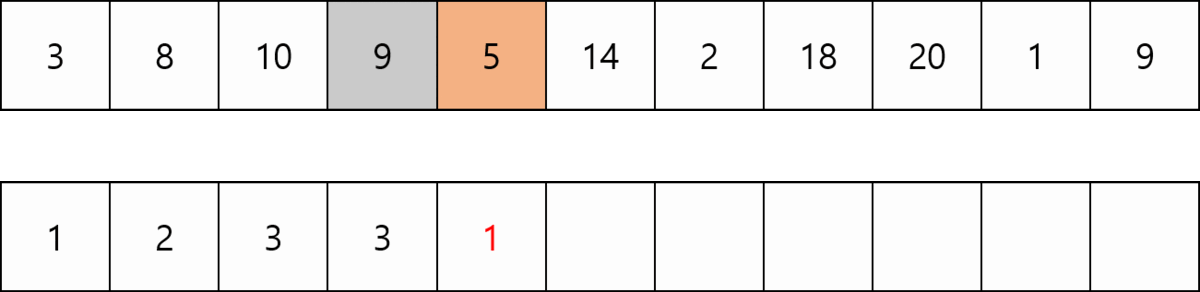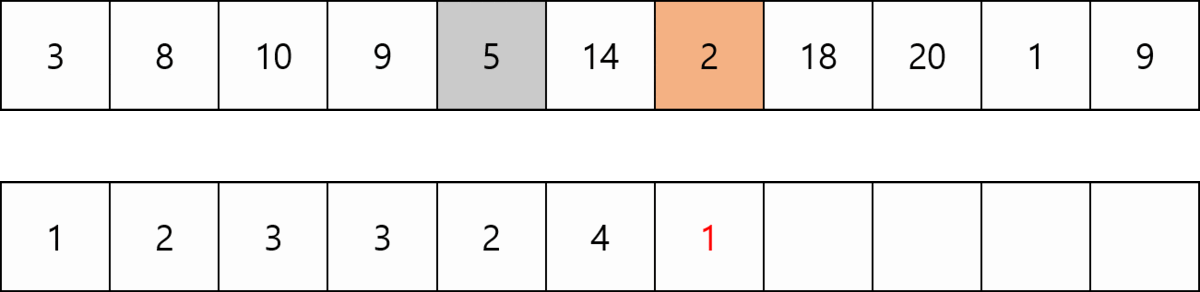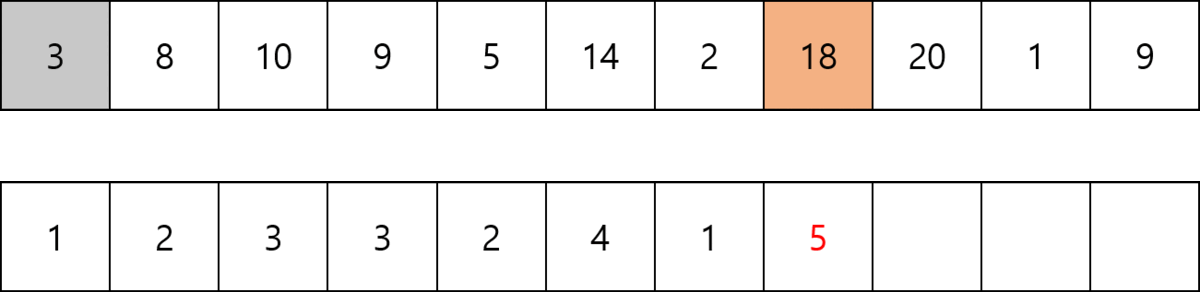
크기가 N인 수열을 돌면서 i 번째에서 i - 1 만큼 탐색하므로 N * (N + 1) / 2번의 연산이 필요하다. 따라서 O(N²)의 시간복잡도를 갖는다.

O(N²)

첫번째 방법의 경우 이해와 구현이 상대적으로 쉽지만 시간복잡도가 크기때문에 10,000 < N 일 경우 시간초과가 발생한다.

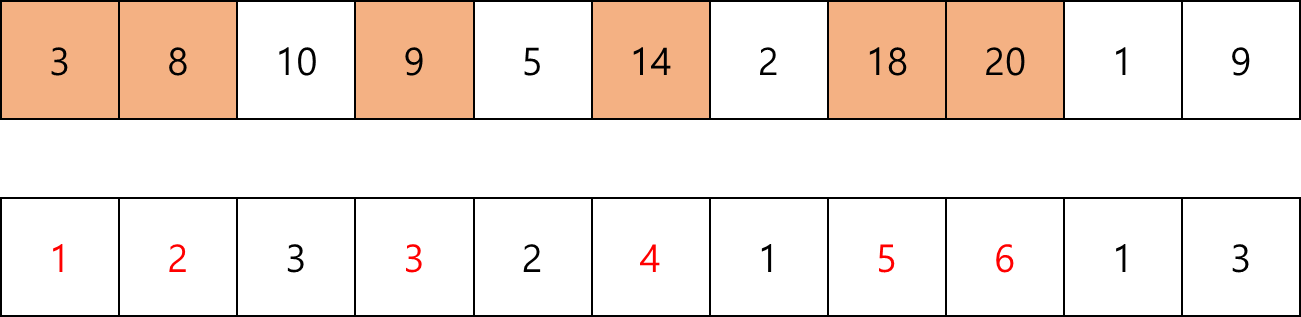
최장 증가 수열의 값을 확인하려면 DP배열의 Max 값의 위치부터 역순으로 탐색하며 이전보다 한개씩 작아지는 위치의 값들을 순차적으로 저장하면된다.

방법(2)

두번째 방법은 DP와 이분탐색을 사용하여 구현한다. DP에 저장되는 값은
DP[i] = k(i <= k <= N)번째 수가 DP[i - 1] < Num[k] < DP[i] 를 만족하는 경우 Num[k]의 값이다.
현재까지의 증가수열의 길이가 같다면 작은 수들로 이루어진 경우가 이후 비교될 숫자들이 연결될수 있는 확률이 높기때문에 작은 숫자가 나올경우 갱신하는 방법이다.

예를들어 다시 [3 8 10 9 5 14 2 18 20 1 9] 수열에서 증가수열은 [3 8 10 ...] 의 경우와
[3 8 9 ...] 의 경우로 나누어진다. 이때 이후에 나오는 수 k에 대해 9 < K < 10일 경우
[3 8 10 ...]와 [3 8 9 k ...]로 수열이 바뀌므로 더 낮은 수의 조합이 유리하다.
DP 배열의 경우 [1 5 9 14 18 20 0 0 0 0 0]이 최종형태이고 최장 증가 수열의 크기는 6이다. 이때 유의해야 할 점은 [1 5 9 14 18 20]이 최장 증가 수열이 아니라는 점이다. 단지 크기를 나타내기 위한 저장값이다.

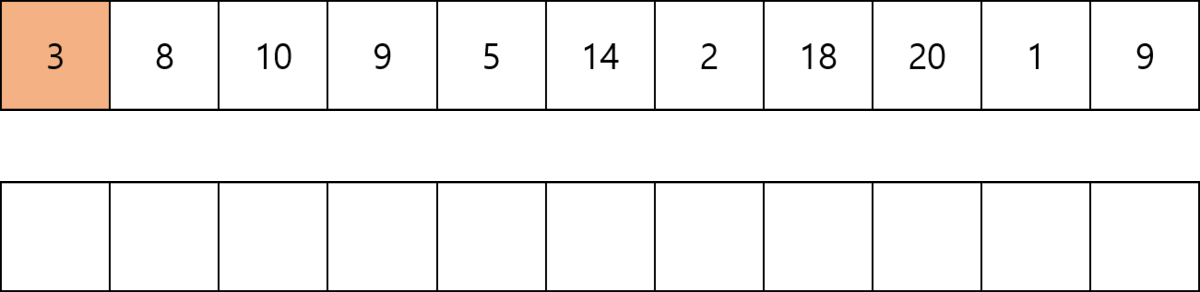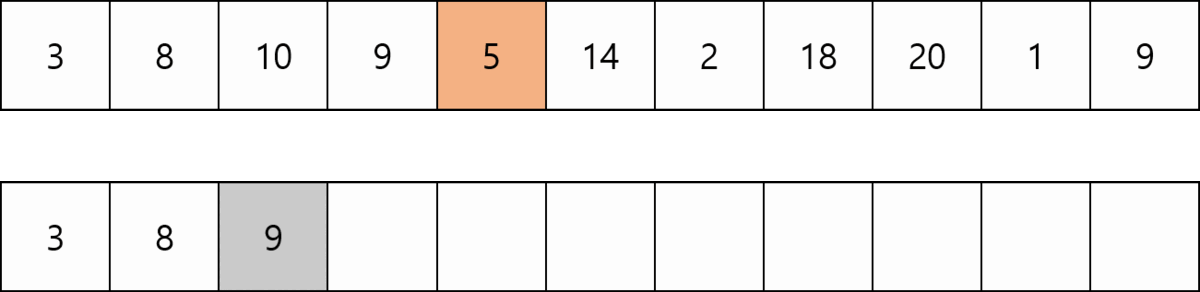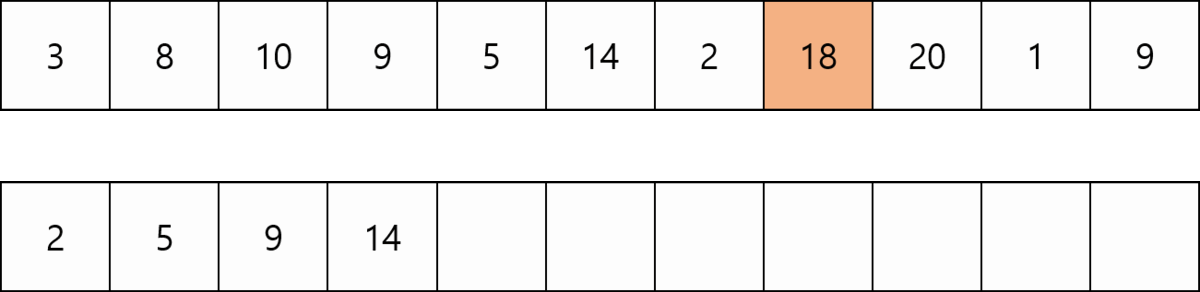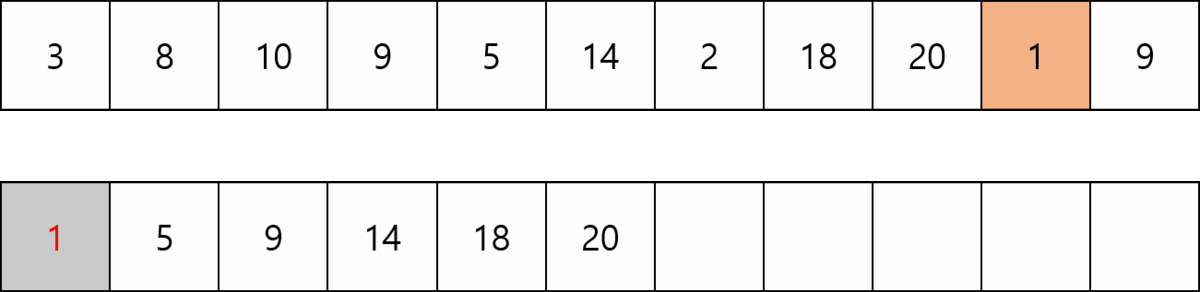
Num 배열에서 k번째 수가 들어갈 자리를 DP 배열에서 탐색하는데 보다시피 DP 배열은 정렬된 상태이다. 정렬된 상태에서 탐색을 하는 경우 이분탐색이 가장 적은 연산을 하므로 최악의 경우 크기가 N인 수열을 돌면서 i번째에서 log i 만큼의 연산이 필요하다. 따라서 O(NlogN)의 시간복잡도를 갖는다.

O(NlogN)

두번째 방법의 경우 시간복잡도가 비교적 작지만 구현이 조금더 복잡하다.

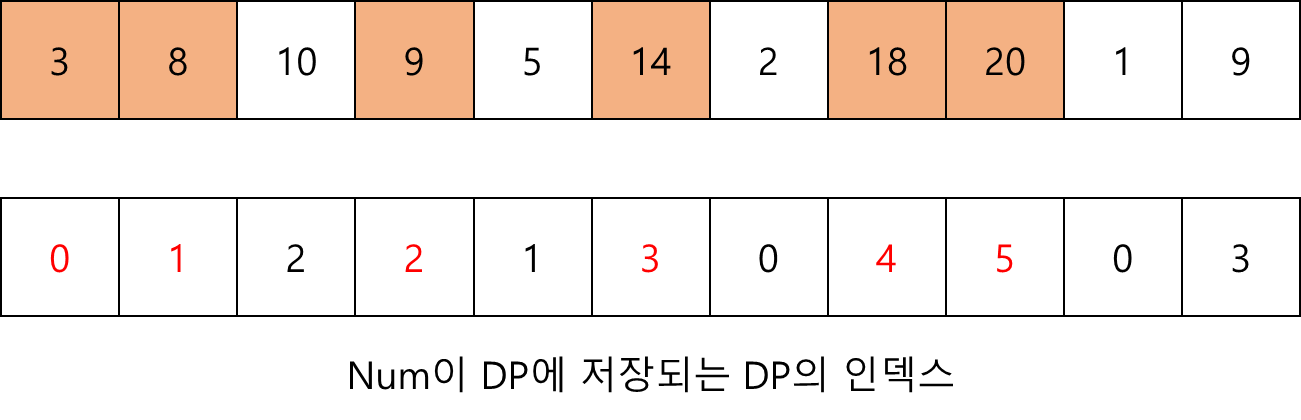
최장 증가 수열의 값을 확인하려면 새로운 배열에 Num 배열의 값이 DP배열에 들어가는 인덱스를 저장해 둔 뒤 인덱스가 가장 큰 위치부터 역순으로 탐색하며 이전보다 한개씩 작아지는 위치의 값들을 순차적으로 저장하면된다.