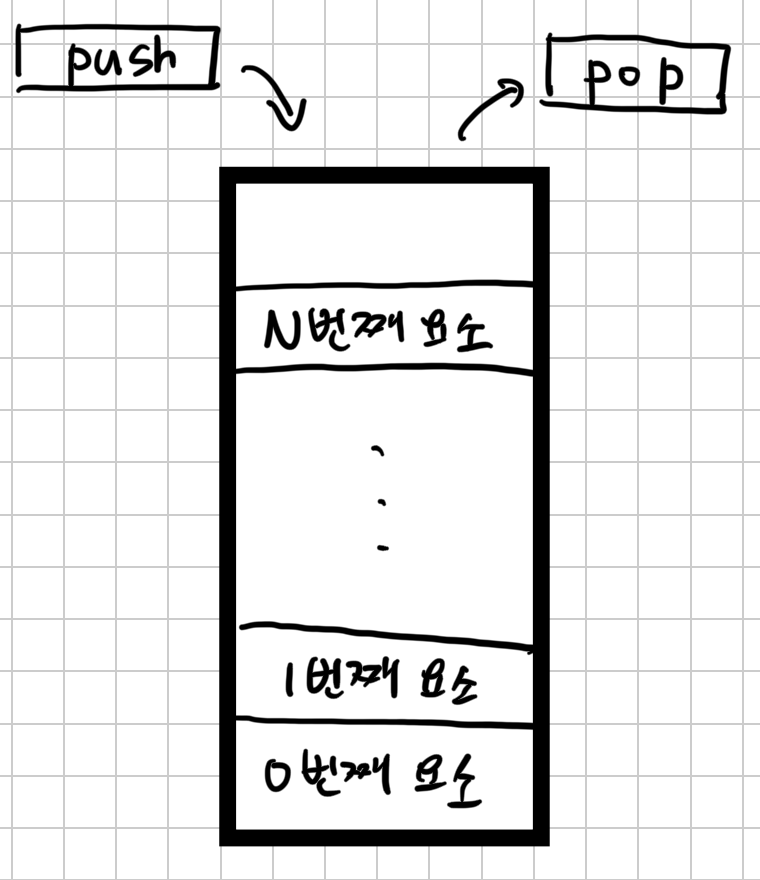
스택(Stack) 이란?
스택은 LIFO(Last In First Out) 구조를 가진 자료구조. 즉,먼저 들어간 데이터는 마지막에
Stack 주요 연산자
-push() : 스택의 맨 위에 요소를 추가한다.
+)반환값 : 스택에 추가된 요소
-pop() : 스택의 맨 위에 있는 요소를 삭제한다.
+)반환값 : 스택에 제거된 요소
-peek() : 스택에서 자료를 삭제하지 않고 반환한다.
+)반환값 : 스택에 있는 요소
-isEmpty() : 스택이 비어있는지 확인하는 메서드
+)비어있으면 true, 가득 차 있으면 false
-search(Objeck o) : 스택에서 지정된 객체가 위에서부터 몇번째 있는지를 반환하는 메서드. 스택의 맨 위에 있는 요소의 위치는 1
+)반환값 : 객체의 위치(1부터 시작), 스택에 객체가 없으면 -1
Stack의 시간복잡도
Stack의 주요 연산들의 시간 복잡도는 보통 O(1)
-push : 스택의 크기에 상관없이 항상 -> O(1)
-pop : 스택의 크기에 상관없이 항상 -> O(1)
-peek : 스택의 크기에 상관없이 항상 -> O(1)
-isEmpty : 스택의 크기에 상관없이 항상 -> O(1)
-search : 스택의 크기에 비례하여 수행시간이 증가. 객체를 찾을때 까지 스택을 순차적으로 검색하기 때문에 최악의 경우 모든 요소를 한번 씩 확인해야 할 수도 있음 -> O(n)
시간복잡도
알고리즘이 n이 되는데 필요한 시간의 대략적인 양을 나타내는 중요한 개념. 이는 입력 크기에 따라 알고리즘의 성능을 평가하는데 사용됨.
시간복잡도 기본 개념
-
빅 오 표기법 (Big-O Notation)
-알고리즘의 최악의 실행 시간을 표현
-입력크기 n에 대한 실행시간의 상한선을 나타냄 -
주요 시간 복잡도 유형
-O(1) : 상수 시간. 입력크기에 관계없이 항상 동일한 시간이 소요됨
-O(log n) : 로그 시간. 이진 탐색과 같은 알고리즘에서 발생
-O(n) : 선형 시간. 입력 크기에 비례하는 시간이 소요됨 ex) 단일루프
-O(n log n) : 로그 선형 시간. 병합정렬, 퀵 정렬의 평균 및 최선 시간 복잡도
-O(n^2) : 이차 시간. 중첩 루프가 있는 알고리즘
-O(2^n) : 지수 시간. 피보나치 수열의 단순 재귀적 구현
-O(n!) : 팩토리얼 시간. 외판원 문제와 같은 조합적 문제
외판원 문제(Traveling Salesman Problem, TSP)란?
외판원 문제는 여러 도시를 방문하고 다시 출발지로 돌아오는 가장 짧은 경로를 찾는 문제.
모든 도시를 정확히 한번씩 방문해야 함. 이 문제를 해결하기 위해 모든 가능한 경로를 계산하는 방법은 팩토리얼 시간 복잡도를 가짐.
예를들어 4개의 도시가 있을때 가능한 경로는
1. A -> B -> C -> D -> A
2. A -> B -> D -> C -> A
3. A -> C -> B -> D -> A
4. A -> C -> D -> B -> A
5. A -> D -> B -> C -> A
6. A -> D -> C -> B -> A
4개의 도시의 경우 총 6개의 경로가 있음. 이를 일반화 하면, n개의 도시가 있을때 가능한 경로의 수는 (n - 1)! 모든 경로를 탐색하는 알고리즘의 시간 복잡도는 O(n!)
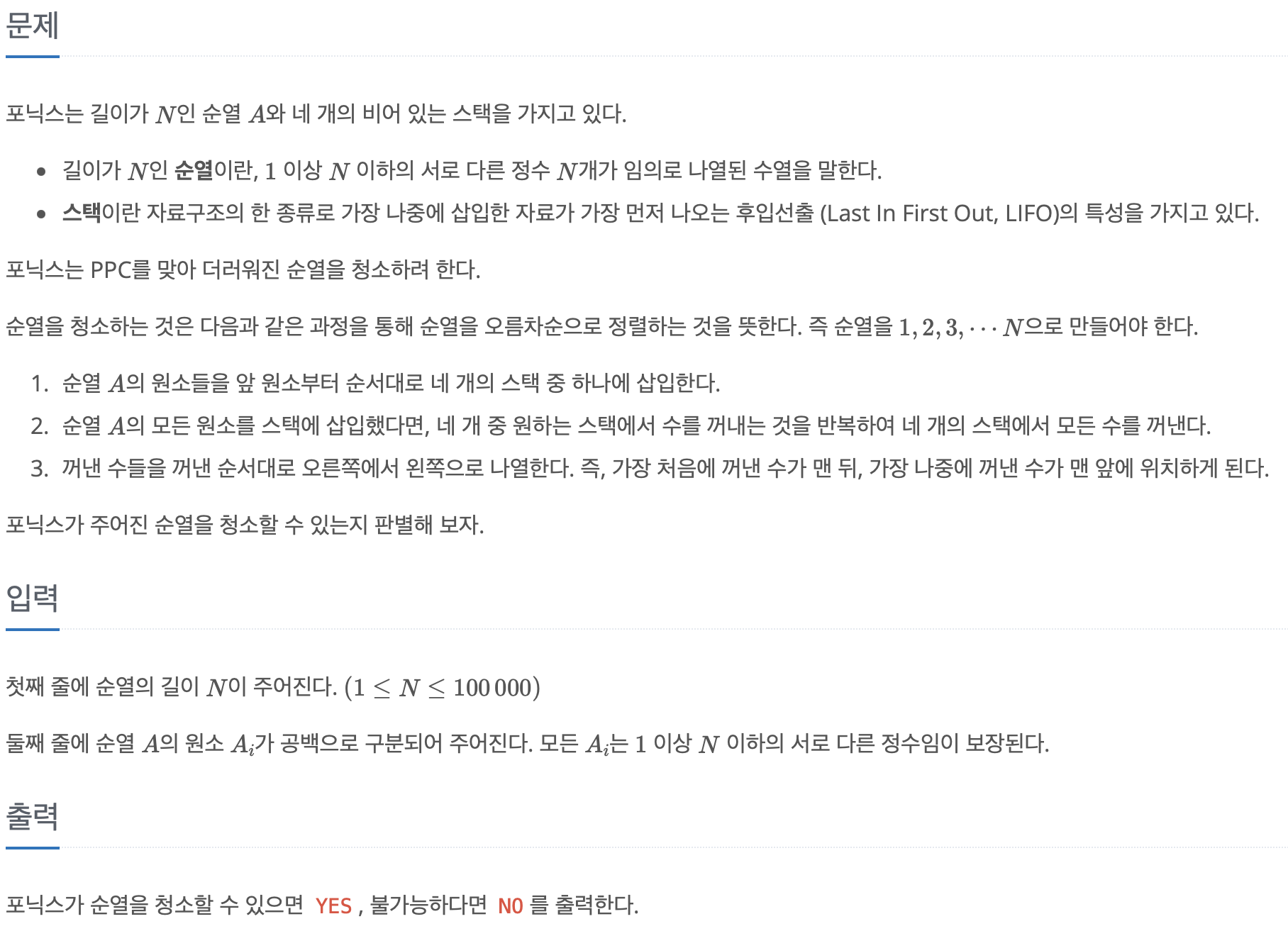
BAEKJOON
25556번 포스택 문제풀이

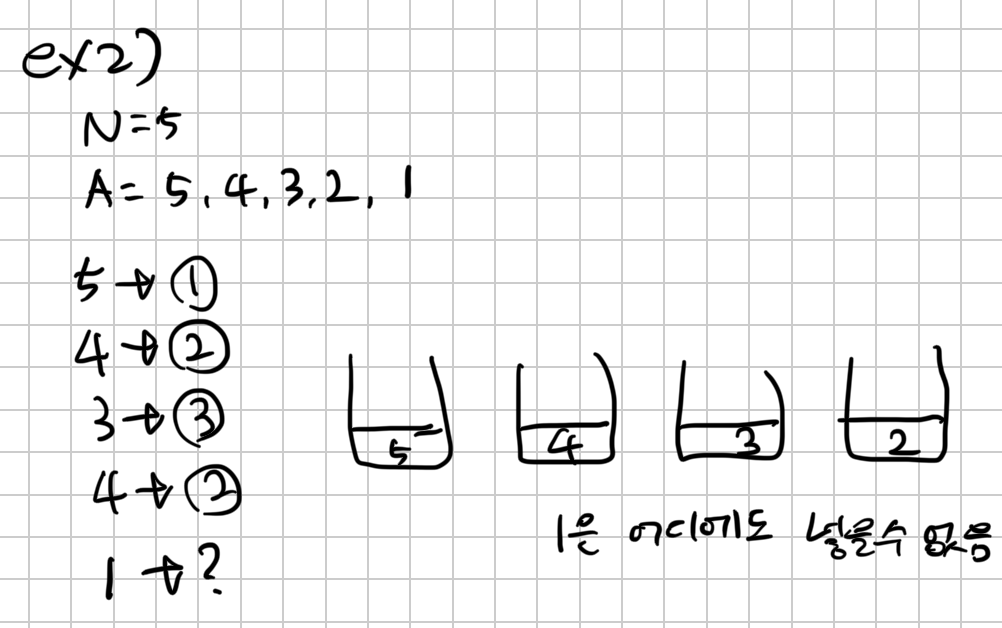
import java.util.Scanner;
import java.util.Stack;
public class Main {
public static boolean stackClean (int N, int[] A) {
Stack<Integer>[] stacks = new Stack[4];
for (int i = 0; i < stacks.length; i++) {
stacks[i] = new Stack<>();
}
for (int i : A) {
boolean placed = false;
for (Stack<Integer> stack : stacks) {
if (stack.isEmpty() || stack.peek() < i) {
stack.push(i);
placed = true;
break;
}
}
if (!placed) {
placed = false;
}
}
int cur = N;
while (cur > 0) {
boolean found = false;
for (Stack<Integer> stack : stacks) {
if (!stack.isEmpty() && stack.peek() == cur) {
stack.pop();
cur--;
found = true;
break;
}
}
if (!found) {
return false;
}
}
return true;
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int N = sc.nextInt();
int[] A = new int[N];
for (int i = 0; i < N; i++) {
A[i] = sc.nextInt();
}
if (stackClean(N, A)) {
System.out.println("YES");
} else {
System.out.println("NO");
}
}
}