Java) 자료구조, 알고리즘

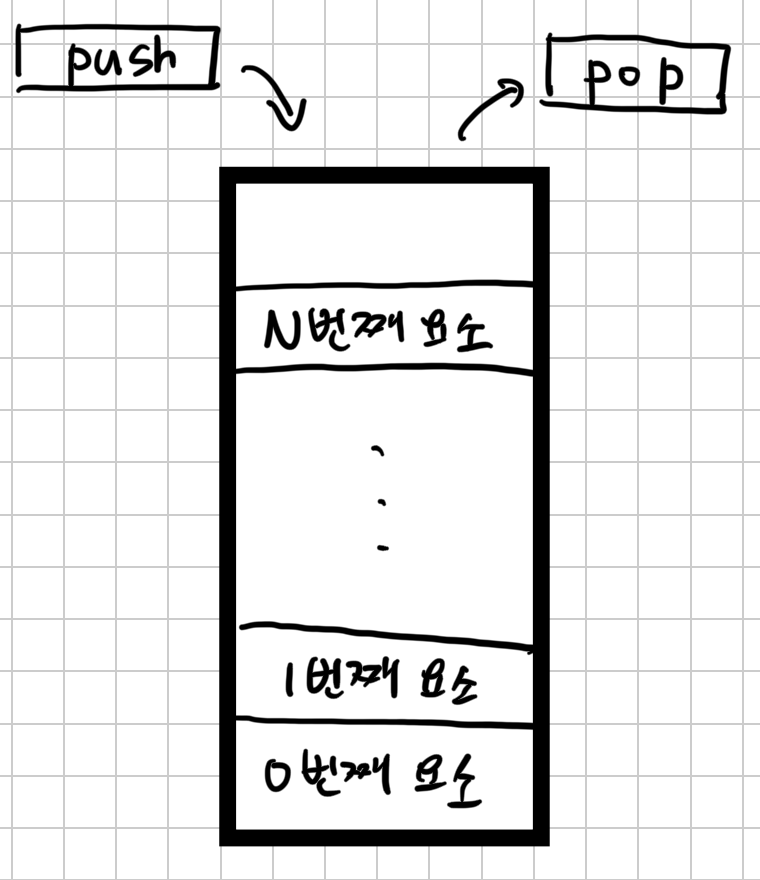
Stack 주요 연산자\-top() : 스택의 가장 위에 있는 자료를 반환한다.\-push() : 스택에 자료를 삽입한다.\-pop() : 스택에서 자료를 삭제한다.\-isEmpty() : 스택에 공간이 여유 있으면 'true', 가득 차면 'false'를 반환한다.\

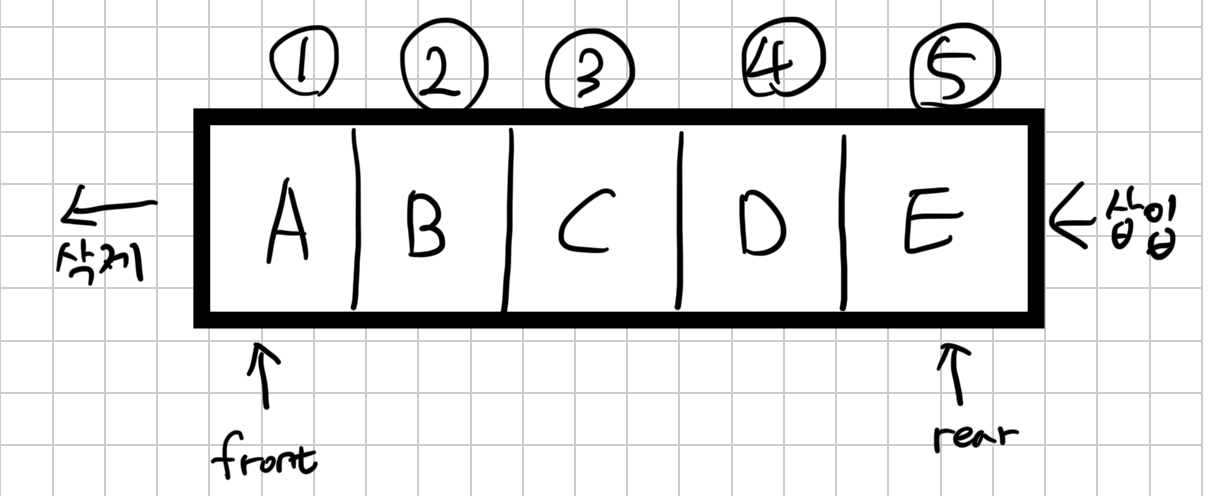
큐는 FIFO(First in First Out) 구조를 가진 자료구조. 즉, 먼저 들어간 데이터가 먼저 나오는 원리\-offer(E e) : 큐의 맨 끝에 요소를 추가\-poll() : 큐의 맨 앞에서 요소를 제거하고 반환\-peek() : 큐의 맨 앞에 있는 요소를

\-멤버변수ArrayList 를 사용하여 스택의 데이터를 저장하는 리스트. 데이터의 추가와 삭제가 용이하고, 동적으로 크기가 조절되기 때문에 스택에 적합한 자료구조\-생성자생성자에서는 ArrayList 인스턴스를 생성하여 초기하함. 따라서 MyStack1 객체를 생성하

Stack과 결과 문자열 초기화\-stack은 문자를 저장할 스택\-result는 역순으로 된 문자열을 저장할 변수문자열을 Stack에 push\-입력된 문자열 str을 split("") 메서드를 사용하여 개별 문자로 분리\-각 문자를 Stack에 push함 예를들어

멤버변수\-ArrayList 타입의 list 멤버변수 선언\-이 요소는 Queue 의 요소를 저장생성자\-MyQueue1 클래스의 생성자\-객체가 생성될 때마다 ArrayList를 초기화하여 빈 Queue를 생성isEmpty() 메서드\-Queue가 비어있는지 여부를

\-주어진 N에 대해 마지막 남은 카드 찾는 메서드\-queue는 LinkedList 를 사용하여 구현된 Queuequeue 초기화\-IntStream.range(1, N + 1) : 1부터 N까지의 정수 스트림을 생성\-forEach(x -> queue.add(x))

클래스 선언 및 멤버 변수\-class MyDeque : deque를 구현하기 위한 클래스\-ArrayList list : deque의 데이터를 저장하는 ArrayList\-MyDeque1() : deque의 생성자. ArrayList를 초기화deque의 비어있는지 확

데이터 재정렬 메서드\-reorederData(int\[] arr) : 배열을 재정렬하는 메서드\-Deque deque = new ArrayDeque() : Deque 자료구조를 초기화\-ArrayList result = new ArrayList() : 결과를 저장할

버블정렬 (Bubble Sort)\-동작원리 : 배열을 반복적으로 순회하면서 인접한 두 원소를 비교하고, 순서가 잘못된 경우 교환. 각 반복(iteration) 마다 가장 큰 원소가 끝으로 이동.\-시간복잡도 : O(n^2)\-두 개의 반복문을 사용하여, 내부 반복문에

mergeSort 함수\-배열을 반으로 나누어 왼쪽과 오른쪽 부분 배열을 재귀적으로 정렬\-left와 right는 현재 정렬할 부분 배열의 시작과 끝 인덱스를 나타냄\-mid는 중간 인덱스로, 배열을 두 부분으로 나누기 위해 사용2.merge 함수\-두 개의 정렬된 부

준비단계\-ArrayList<Queue<Integer>> list 는 0부터 9까지의 10개의 큐를 저장. 각 큐는 해당 자릿수의 값에 해당하는 숫자를 저장2.최대 자릿수 계산\-getMaxLen(int\[] arr) 메서드는 배열에서 가장 큰 숫자의 자릿수

입력 배열이 null 이거나 길이가 0 이면 바로 반환cnrArr 배열을 만들어 0, 1, 2의 갯수를 세어줌cntArr 를 이용해 원래 배열을 정렬된 형태로 재구성입력 검사\-입력 배열이 null 이거나 비어있는 경우, 빈 ArrayList를 반환해시맵 생성\-문자열

배열은 같은 타입의 여러 값을 하나의 변수에 저장할 수 있는 자료구조.배열은 고정된 크기를 가지며, 한번 생성되면 크기를 변경할 수 없음배열을 선언하려면 배열의 타입과 배열의 이름을 지정.정수형 배열을 선언하는 예제)또는두 방법 모두 유효하지만 일반적으로는 int\[]

키(key) - 값(value) 쌍을 저장하는데 사용되는 자료구조. 빠른 검색, 삽입, 삭제 성능을 제공. HashMap은 키를 해시하여 값을 저장하기 때문에 키와 값은 고유해야함\-key, value : key는 중복될수 없으며, 각 key는 하나의 value에 매핑

\-양방향 연결리스트를 구현한 클래스\-LinkedList 는 List 인터페이스와 Deque 인터페이스를 모두 구현하여 List, Queue, Stack의 기능을 모두 사용할 수 있음.\-Node(노드) 기반의 자료구조로, 각 Node는 데이터와 다음 및 이전 Nod

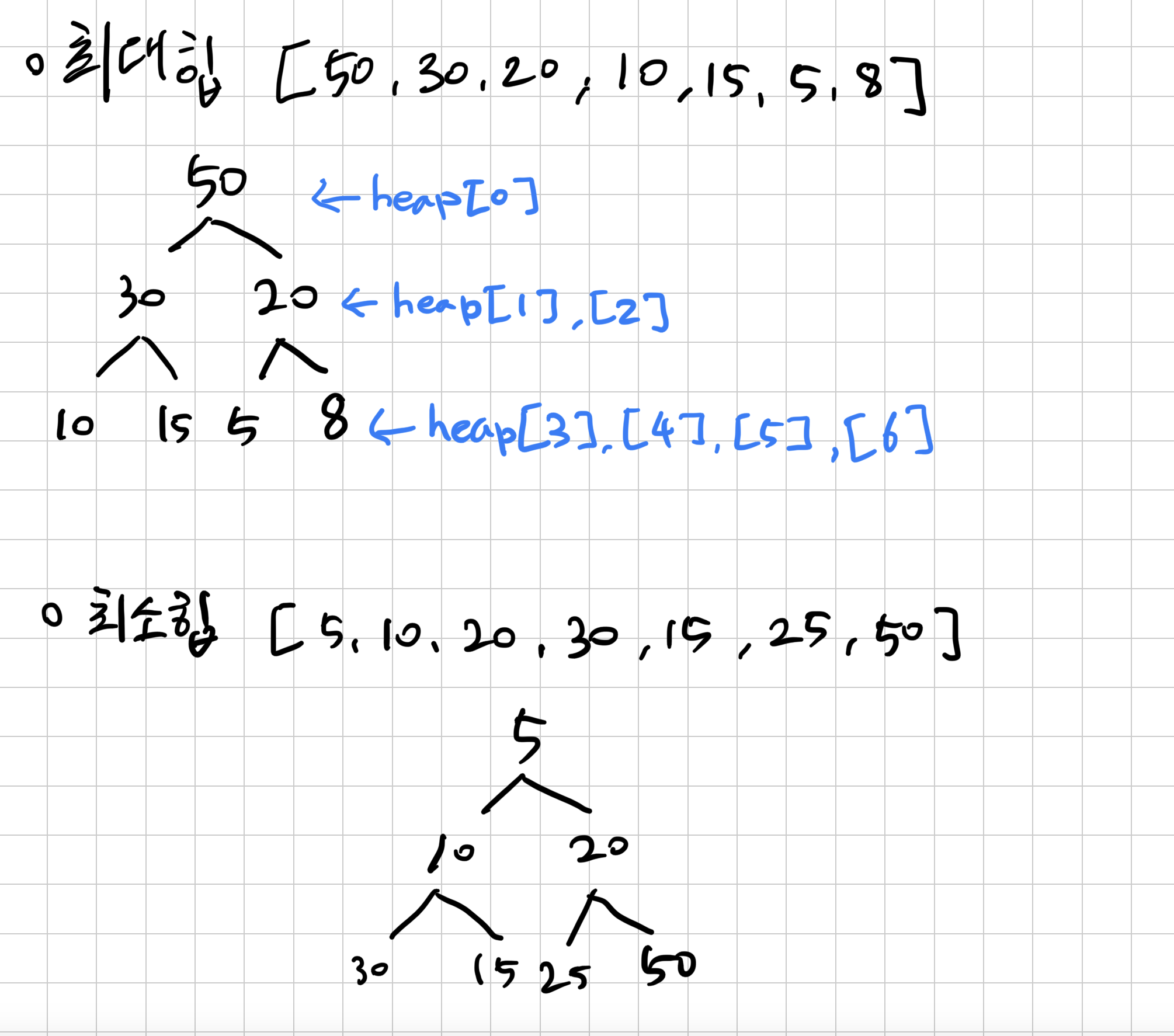
\-특정한 조건을 만족하도록 구성된 Complete Binary Tree(완전 이진 트리)\-Heap에는 Max Heap(최대 힙), Min Heap(최소 힙) 두가지 종류가 있음\-Heap은 Prioruty Queue(우선순위 큐)를 구현하는데 사용됨완전 이진 트리

정렬된 배열에서 특정 값을 찾는 효율적인 방법으로, 시간복잡도는 O(log n)left 와 right 포인터를 배열의 처음과 끝으로 초기화while 반복문을 이용하여 left가 right보다 작거나 같은 동안 반복mid 포인터를 배열의 중간 위치로 계산target 값이

배열 검증 : 먼저 입력된 배열이 null 이거나 길이 0인지 확인. 그렇다면 -1을 반환이진 탐색 루프 while (left <= right) 루프에서 배열의 중간 위치를 계산하여 target 값과 비교\-target이 중간 값과 같다면, 해당 인덱스를 반환\-

알고리즘 - 투 포인터 투 포인터(Two pointers) 란? 배열이나 리스트에서 두 개의 포인터를 이용하여 원하는 결과를 찾거나 주건을 만족하는 부분을 찾는 알고리즘 기법. 주로 정렬된 배열에서 특정 합을 갖는 부분 배열을 찾거나, 두 요소의 합이 특정 값과 같은지

입력 검사\-문자열 s가 null 이거나 길이가 0인 경우 null을 반환양 끝에서부터 비교\-문자열의 양 끝에서부터 시작하여 같은 문자를 찾음. p1은 문자열의 시작부터, p2는 문자열의 끝부터 시작문자 비교 및 제거\-p1 과 p2가 가리키는 문자가 같은동안 반복\

LinkedList(연결리스트) 란?\-양방향 연결리스트를 구현한 클래스\-LinkedList 는 List 인터페이스와 Deque 인터페이스를 모두 구현하여 List, Queue, Stack의 기능을 모두 사용할 수 있음.\-Node(노드) 기반 자료구조로, 각 Nod

\-연결 리스트의 단일 요소를 나타냄\-data : 노드가 저장하는 정수 데이터\-next : 다음 노드를 가리키는 참조\-생성자 : Node(int data, Node next) 는 주어진 데이터와 다음 노드 참조로 노드를 초기화\-단일 연결 리스트를 나타냄\-hea

해시테이블은 데이터를 저장할 때 키(key)에 대한 해시함수를 적용하여 데이터가 저장될 인덱스를 계산하고, 이 인덱스를 활용하여 데이터에 접근하는 자료구조.빠른 검색 및 삽입 : HashTable 은 평균적으로 O(1) 의 시간 복잡도를 가지며, 매우 빠른 검색과 삽입

Hashtable<Integer, Integer> ht = new Hashtable<>(); : 해시 테이블을 생성. 키와 값 모두 Integer 타입ht.put(arr1i, arr1i); : 첫 번째 배열의 각 원소를 해시 테이블에 키와 값으로 저장ht.c

트리(Tree) 란? 계층적 구조를 나타내는 자료구조로, 루트(Root) 노드에서 시작하여 자식(Children) 노드로 확장되는 방식으로 구성. 트리는 다양한 컴퓨터 과학 및 알고리즘 문제에서 중요한 역할을 함. 트리의 기본 개념 노드(Node) : 트리의 기본 구

정점(Vertex)와 간선(Edge)으로 구성된 자료구조.다영한 관계와 연결을 표현하는데 사용되며, 컴퓨터 과학과 수학에서 중요한 역할을 함.\-정점(Vertex) : 그래프에서의 개체 또는 노드. 보통 V로 표시\-간선(Edge) : 두 정점을 연결하는 선. 보통 E

우선순위 큐(Priority Queue) 란? 각 요소가 우선순위를 가지고 있는 자료 구조로, 일반적인 큐와 달리 우선순위가 높은 요소가 먼저 처리됨. 우선순위 큐는 힙(Heap) 자료구조로 구현되는 경우가 많으며, 이진 힙(Binary Heap) 을 많이 사용함.

각 단계에서 최적의 선택을 하여 전체 문제의 최적해를 구하는 알고리즘.항상 최적해를 보장하지 않지만, 많은 경우에 대해 빠르고 간단한 해법을 제공. 특히, 그리디 알고리즘이 최적해를 제공하는 문제를 탐욕적 최적 부분 구조를 가진다고 함.문제 분해 : 문제를 여러개의 하

문제를 작은 하위 문제로 나누어 각각을 해결 한 후, 이들을 합쳐 전체 문제의 해결책을 얻는 알고리즘 설계 비법.분할(Divide) : 문제를 더 작은 하위 문제로 나눔정복(Conquer) : 각 하위 문제를 재귀적으로 해결결합(Combine) : 하위 문제의 해를 합

그래프에서 두 노드 간의 최단경로를 찾는 문제를 해결하는 알고리즘.다양한 응용 분야에서 중요한 역할을 하며, 가장 많이 사용되는 알고리즘으로는 다익스트라 알고리즘, 벨만 - 포드 알고리즘, 플로이드 - 위셜 알고리즘 등이 있음비음수 가중치 그래프에서 단일 출발점에서 다

알고리즘의 성능을 측정하는데 사용되는 중요한 개념. 이는 입력 크기에 따라 알고리즘이 실행되는 시간의 양을 나타냄. 시간 복잡도는 주로 Big - O 표기법을 사용하여 표현됨.Big - O 표기법은 알고리즘의 최악의 경우 성능을 나타내며, 가장 중요한 요소에 따라 실행

1. 정렬 알고리즘 (Sorting Algorithms) 버블 정렬 (Bubble Sort) 기본 개념 : 인접한 두 요소를 비교하여 큰 값을 뒤로 보냄. 이 과정을 반복하여 정렬 장점 : 구현이 매우 간단함 단점 : 매우 비효율적. 시간 복잡도가 높아 큰 데이터셋에는

주로 문자열을 저장하고 검색하는 데 사용되는 효율적인 자료구조. 트라이는 특히 사전과 같은 어휘 집합을 관리하거나, 자동완성, 패턴 매칭 등의 응용 프로그램에서 유용.트라이는 트리 형태의 자료구조로, 각 노드는 하나의 문자를 나타내며, 루트 노드는 비어있음. 문자열의

가능한 모든 후보해를 탐색하면서 해결책을 찾는 알고리즘 기법.일반적으로 깊이 우선 탐색(DFS) 를 기반으로 하며, 모든 가능성을 탐색하다가 현재 경로가 해결책으로 이어질 수 없는 경우, 그 경로를 포기하고 이전 상태로 돌아가 다른 경로를 탐색상태 공간 트리 (Stat

하나의 연결된 그래프에서 모든 정점을 포함하면서 모든 간선의 가중치 합이 최소가 되는 트리.여기서 가중치는 각 간선에 부여된 비용이나 거리를 의미연결성 : 최소 신장 트리는 그래프 내의 모든 정점을 포함하며, 모든 정점 사이에 경로가 존재비용 최소화 : 간선의 가중치

최적화 문제를 해결하는 방법 중 하나로, 중복되는 계산을 피하고 효율적으로 문제를 해결할 수 있는 방법.주로 최적 부분 구조(Optimal Substructure) 와 중복되는 부분 문제(Overlapping Subproblems) 를 가지는 문제에 적용최적 부분 구조