독립변수의 선형결합을 이용해 '사건의 발생 가능성을 예측'하는데 사용되는 기법으로 분류에 속한다. 두 개의 카테고리로 분류되는 범주형 데이터에 적합하다.

Logistic Regression(로지스틱회귀)

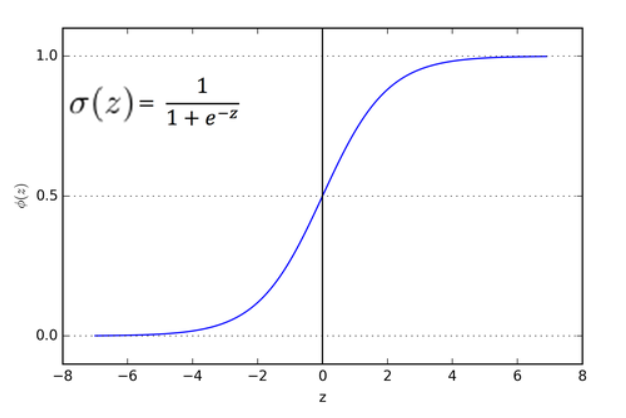
sigmoid function($\sigma(z)$)으로 회귀식을 사용하지만 0.5를 기준으로 0 or 1로 나누어서 관측치가 어디에 속하게 되는지를 계산하는 분류문제로 만들어준다. 확률값이 정해진 기준값 보다 크면 1 아니면 0 이라고 예측한다.

특성변수를 로지스틱 함수형태로 만들어서 결과적으로 관측치가 특정 클래스에 속할 확률값을 나타내게 한다.

기준값(threshold)은 defualt로 0.5로 설정하는 것이 일반적이지만, data imbalance 문제가 있다면 조정해줄 수 있다.

평가지표로는 $R^2$가 아닌, Accuracy(정확도)를 사용한다.
$Acc$ = $\frac{TP + TN}{P+N}$
TP = True Positive (참이 사실일 때 참으로 판단 것)
TN = True Negative (거짓이 사실일 때 거짓으로 판단 것)
P = Positive (참이라고 판단한 것)
N = Negative (거짓이라고 판단한 것)

평가지표 정확도에 관하여

Logit transformation

로지스틱 함수가 비선형이기 때문에 계수를 직관적으로 해석하기 어려울 때가 많다. 이를 위해서 $Odds$를 사용하여 선현결합의 형태로 계수를 쉽게 해석할 수 있다.

$Odds$ = $\frac{p}{1-p}$ = 실패확률에 대한 성공확률의 비
p = 성공확률, 1-p = 실패확률

p = 1 일때 odds = $\infty$
p = 0 일때 odds = 0

$\large ln(Odds) = ln(\frac{p}{1-p}) = ln(\frac{\frac {1}{1+e^{-(\beta _{0}+\beta _{1}X_{1}+\cdots +\beta _{p}X_{p})}}}{1 - \frac {1}{1+e^{-(\beta _{0}+\beta _{1}X_{1}+\cdots +\beta _{p}X_{p})}}}) = \normalsize \beta _{0}+\beta _{1}X_{1}+\cdots +\beta _{p}X_{p}$

이렇게 오즈에 로그를 취해 변환하는 것을 로짓변환(Logit transformation) 이라고 한다. 비선형형태인 로지스틱 함수 형태를 선형형태로 만들어 회귀계수의 의미를 해석하기 쉽게 만드는 것이다. 이러한 Logit Transformation은 특성 X의 증가에 따라 로짓($ln(Odds)$)가 얼마나 증가 혹은 감소했다고 해석을 할 수 있게 된다. 이 로짓을 바탕으로 선형회귀를 한 것이 바로 로지스틱 함수인 것이다.

분류 문제의 Baseline model(기준 모델)

python으로 구현하기ㅣ

1. 데이터 전처리
   a. 결측치 처리, 특성 feature 고르기, 학습/평가 데이터 분리하기 등
   b. 인코딩, 스케일링 하기(fit_transform, transform)
   - encode fit은 각 속성(feature)마다 컬럼을 만드는 작업으로 fit은 학습을 하는 작업이다.
   - transform을 통해 데이터를 변형한다.
   - 학습세트로 fit을 한 번 해주었기 때문에, 평가세트에서는 별도로 fit을 할 필요 없이 바로 transform

2. 모델 생성 및 평가