💛 Vector Transformation (벡터 변환)

2차원의 공간에서 벡터를 변환하는 것, 즉, 선형 변환은 임의의 두 벡터를 더하거나 혹은 스칼라 값을 곱하는 것을 의미한다.

• 임의의 두 벡터 더해서 방향 바꾸기: $T(u+v)$ = $T(u)+T(v)$
• 스칼라 값을 곱해서 크기 바꾸기: $T(cu)$=$cT(u)$

선형변환은 선형 결합을 보존하는, 두 벡터 공간 사이의 함수이다.
선형 결합을 보존한다는 것은 위의 덧셈과 곱셈의 성질을 가지고 있다는 것이고 두 벡터 공간 사이의 함수라는 것은 한 점을 한 벡터공간에서 다른 벡터공간으로 이동시킬 때 적용하는 이동 규칙을 의미한다. 참고블로그

선형투영(Linear Projection)도 일종의 vector transformation이다.

임의의 $\mathbb{R}^2$ 벡터를 다른 $\mathbb{R}^2$ 내부의 벡터로 변환하는 과정은 특정 $T$라는 매트릭스를 곱하는 것과 동일한 과정이다. 즉, transformation은 matrix를 곱하는 것을 통해 벡터(데이터)를 다른 위치로 옮긴다라는 의미를 가지고 있다.

벡터 transformation은 선형, 즉, 곱하고 더하는 것으로만 이뤄진 transformation이기 때문에 매트릭스와 벡터의 곱으로 표현할 수 있다.

이는 벡터를 더하거나 곱하는 것만으로도 벡터의 방향과 크기를 바꿀 수 있는 linear transpormation에서 가능한 것이다. 또한 어떤 매트릭스를 매트릭스의 곱으로 표현할 수 있다는 것을 의미한다.

---

🍎 벡터 변환으로써의 매트릭스 - 벡터의 '곱'

• f라는 transformation을 사용해서 임의의 벡터 [x1, x2]에 대해서 [2x1+x2, x1-3x2]로 변환한다고 한다면 다음과 같이 표현할 수 있다.

$f([x_1,x_2]$) = $[2x_1+x_2,x_1 - 3x_2]$

여기에서 임의의 벡터 [x1, x2]는 단위벡터를 이용해서 아래처럼 분리할 수 있다.
$x_1\cdot\hat{i} + x_2\cdot\hat{j}$
이렇게 분리된 각각의 유닛벡터는 transformation을 통해 2x1과 x1, 그리고 x2와 -3x2가 나와야 했다. 이를 매트릭스의 형태로 합치게 되면

$T$ = $[{2, 1}\\{1 -3}]$
이런 매트릭스를 얻을 수 있다. 이 매트릭스를 임의의 벡터에 곱했을 때 transformation이 원하는 대로 이루어진다.

---

💛 eigenvalue & eigenvactor

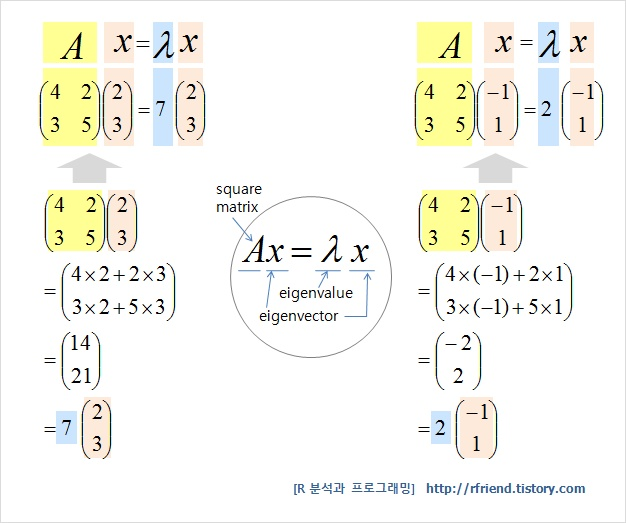
정방행렬 A에 대하여 Ax = λx (상수 λ) 가 성립하는 0이 아닌 벡터 x가 존재할 때, 상수 λ 를 행렬 A의 고유값 (eigenvalue), x 를 이에 대응하는 고유벡터 (eigenvector) 라고 한다.
출처: R 분석과 프로그래밍

위의 출처에서 고유벡터와 고유값의 의미와 이를 기하학적으로 표현하는 법 등에 대해 매우 잘 설명되어 있었다!

🍏 고유벡터(Eigenvector)

• 주어진 transformation에 대해서 크기만 변하고 방향은 변화하지 않는 벡터.
• transformation에 영향을 받지 않는 회전 축 혹은 벡터를 공간의 고유벡터라고 부른다.

🍏 고유값(Eigenvalue)

고유벡터가 주어진 transformation에 대해서 변하는 크기는 스칼라값으로 변화하게 되는데 이 특정 스칼라값을 고유값이라고 한다.
$T \cdot v = v'= \lambda\cdot v$

💎 데이터를 변환하는 목적의 단계 중 하나인 vector transformation

매우 다양한 방법으로 transformation을 할 수 있는데, 그 중 어떤 목적으로, 어떤 transformation을 하는가에 따라서 고유값이 하나의 선택지가 된다.

벡터를 변환할 때, 데이터를 변환할 때 수많은 선형 변환을 할 수 있으니 그 중 선택을 해야하는데 어떤 기준을 가지고 변환할 것인가? -> 고유벡터를 기준으로 변하지 않는 축을 가지고 변환하게 된다. 단, 데이터가 고차원이 될수록 데이터 변환에 문제가 생긴다.

❓ 고유벡터 vs 기저벡터

고유벡터와 기저벡터는 상관관계가 없다.

기저벡터: 벡터가 충분히 있고 선형 독립적이기만 하다면 기저벡터는 임의로 선정할 수 있다.

고유벡터: 해당 벡터 공간에 대한 '선형 변환(linear transformation)의 특성'이다. 선형 변환마다 고유벡터가 다를 수 있다.

고유백터는 기저벡터와 독립이며, 기저벡터는 모든 변환의 고유벡터와 독립이다.

고유벡터와 기저벡터의 상관관계

💎 고차원의 문제(The curse of Dimensionality)

feature의 수는 일반적으로 몇 개면 많다, 몇 개면 적절하다고 할 수 있는 기준은 없다. 같은 데이터라고 하더라고 내가 해결하고자 하는 문제와 그것을 해결하고자 하는 방법에 따라 선택할 수 있는 feature가 달라지기 때문이다. 하지만 극단적으로 많은 feature의 경우 데이터셋을 모델링하는 데에 문제가 있을 수 있다.

feature가 늘어날수록 표현해야하는 차원이 늘어나지만 인간의 뇌는 3차원 이상의 정보를 공간적으로 다루는 것이 거의 불가능하다. 이는 여러 차원의 데이터셋을 다루는 데에 문제가 된다.

데이터셋에서 인사이트를 찾기 위해 쓰이는 모든 feature가 동일하게 중요하지는 않다. feature를 추가로 사용하는 것이 실제로 얼마나 의미있게 더 좋은 결과를 모델링하는지 고민해봐야한다.

데이터의 일부를 제한하더라도 의미 파악에는 큰 차이가 없다면 feature의 수를 늘리는 것은 어느 시점에서 비효율적이게 된다.

데이터를 많이 쓴다고 해서, feature가 많다고해서 데이터 분석이 더 의미있어지는지 고민해야하낟. 추가로 feature를 사용하면 어떤 데이터셋을 분석하고 모델링을 하여 인사이트를 찾는다고 할 때 모든 feature가 동일하게 중요한 것이 아니다. 덜 중요한 feature를 사용하는 것이 그것을 사용하기 위해 들어가는 resource(모델을 복잡하게 만드는 데에 드는 비용)에 비해 효용이 낮다면 빼도 될 것이다. 고양이를 네모로만 표현해도 고양이라고 인식할 수 있다던가 어순을 바꿔서 정확하지 않고 많은 정보가 생략되어 있지만 의미 파악이 가능하다는 점을 생각해보면 feature의 수를 제한하더라도 의미 파악을 잘 할 수 있다.(dilusion)

feature의 수가 샘플의수보다 많으면 트레이닝 데이터에서의 모델의 설명력이 높지만 실제 데이터에서는 좋지 않을 수 있다.