💛 Dimension Reduction
빅데이터인 데이터셋의 feature가 많으면 많을수록데이터의 시각화나 탐색은 어려워지고 모델링에서도 overfitting의 이슈가 발생하는 등 많은 문제가 발생한다.
차원 축소를 하는 이유
- 시각화 (Visualization)
- 노이즈 제거(Reduce Noise)
- 메모리 절약(Preserve useful info in low memory)
- 퍼포먼스 향상(Improve Performance)
이러한 문제를 해결하면서 빅데이터가 줄 수 있는 인사이트를 도출할 수 있도록 적절한 처리를 하는 방법 중 하나가 바로 차원 축소, dimension reduction이다. dimension reduction에는 다양한 방법들이 지금도 개발되고 있다. dimension reduction은 크게 두 가지로 볼 수 있다.
🖤 Feature Selection
덜 중요한 feature를 물리적으로 제거하자.
데이터셋에서 덜 중요한 feature를 제거하는 방법
🖤 Feature Extraction
기존의 feature를 조합해서 화학적으로 줄이자.
기존에 있던 feature 혹은 기존의 feature들을 바탕으로 조합된 feature를 사용하는 것이다.PCA도 feature extraction의 일종으로 볼 수 있다.
❗️selection과 extraction의 차이
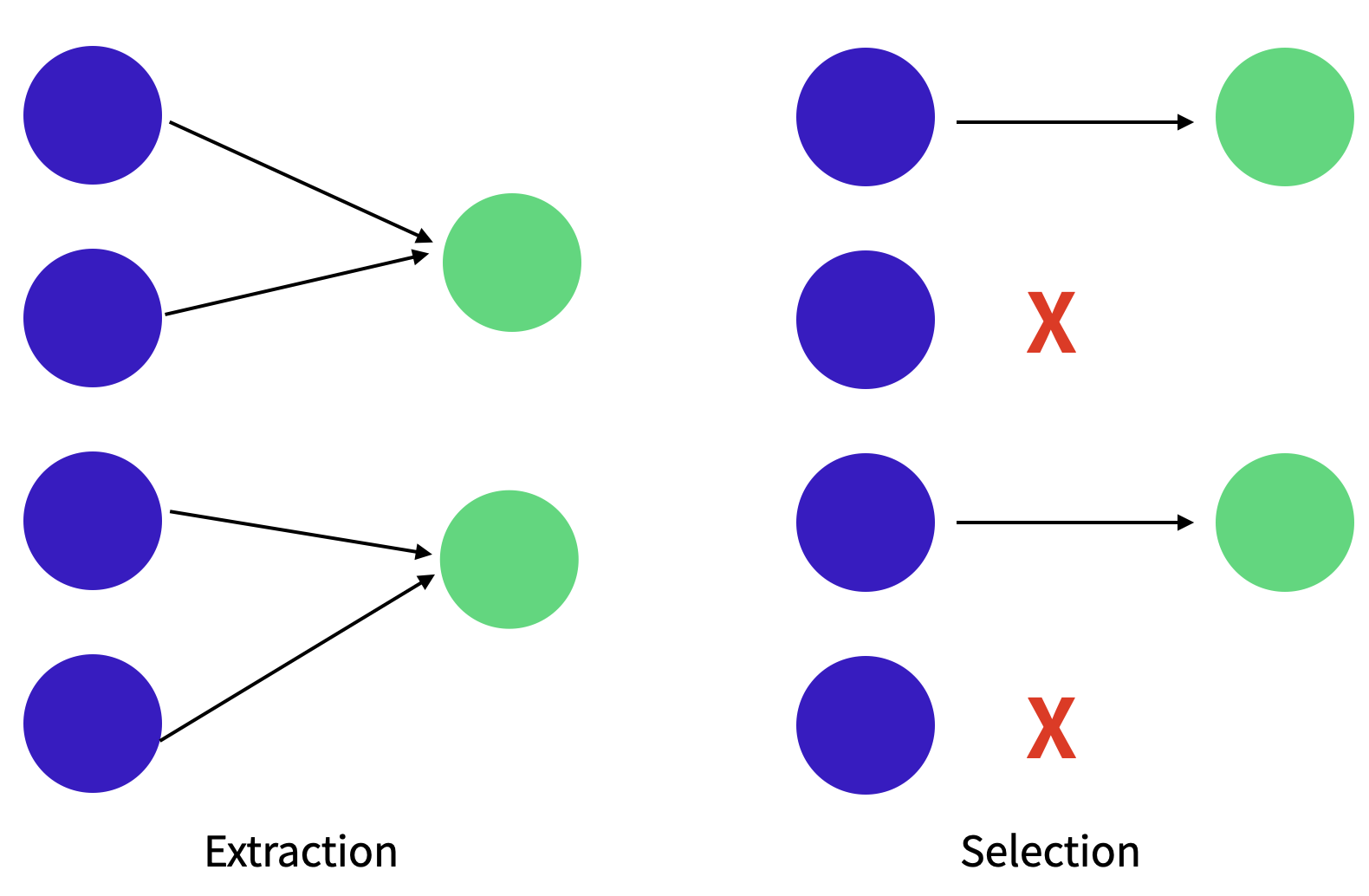
selection
- 장점: 선택된 feature 해석이 쉽다.
- 단점: feature들간의 연관성을 고려해야 한다.
- methods: LASSO, Genetic algorithm 등
extraction
- 장점: feature들간의 연관성을 고려하면서 feature 수를 줄일 수 있다.
- 단점: feature의 해석이 어려움
- methods: PCA, Auto-encoder 등
💛 Principal Component Analysis(PCA)
데이터의 분산(variance)을 최대한 보존하면서 서로 직교하는 새 축(PC)을 찾은 뒤 고차원 공간의 표본들을 선형 연관성이 없는 저차원 공간으로 변환하는 기법으로 어떤 축(PC)이 유의미한지 우선선위를 구할 때 사용한다.
- 고차원의 데이터를 효과적으로 분석하기 위한 기법
- 낮은 차원으로 차원축소
- 고차원 데이터를 효과적으로 시각화 +clustering
- 원래 고차원 데이터의 정보(분산)을 최대한 유지하는 벡터를 찾고, 해당 벡터에 대해 데이터를 (linear) projection하여 데이터의 흩어진 정도를 가장 크게 하는 벡터축으로 삼는다.
➡️ 공분산 행렬의 고유값과 고유벡터를 구한다.
-원 데이터(original data)의 분산을 최대한 보존하는 축을 찾아 투영(projection)하기 위해 사용한다.
- 분산을 최대한 보존하기 위해 퍼져있는 데이터에 대해 독립적인 축을 찾는데 사용한다.
- 분류/예측 문제에 대해서 데이터의 라벨을 고려하지 않기 때문에 효과적으로 데이터를 분리하기가 어렵다. 이러한 경우에는 PLS를 사용한다.
- 데이터의 분포가 정규성을 띄고 있지 않는 경우 적용이 어렵다.
🖤 데이터의 분산 == 정보
데이터가 유의미한 정보를 많이 가지고 있다
= 데이터의 분산이 크다
= 데이터가 차이가 있어 다르다.
💜 PCA Process
PCA 과정을 차근차근 설명한 블로그
차원축소와 PCA 등을 잘 설명한 블로그
1️⃣ 데이터 준비하기
아래는 임의의 데이터를 만든 것이다.
np.array([[벡터1],[벡터2]]) 라는 점 잊지 말자! 괄호 조심.
import numpy as np
X = np.array([[0.2,5.6,3.56],
[0.45,5.89,2.4],
[0.33,6.37,1.95],
[0.54,7.9,1.32],
[0.77,7.87,0.98]])2️⃣ 각 열에 대해서 평균을 빼고, 표준편차로 나누어서 Normalize하기
standardized_data = (X - np.mean(X, axis =0))/np.std(X, ddof=1, axis=0)3️⃣ Z의 분산~공분산 매트릭스 계산하기
를 통해 구할 수 있다.
normalized된 매트릭스(Z,여기에서는 standardized_data)에 대해서 공분산 매트릭스를 구한다.
covariance_matrix = np.cov(standardized_data.T)4️⃣ Z의 분산~공분산 매트릭스의 고유벡터와 고유값 계산하기
분산을 가장 크게 하는 축을 찾는다는 의미이다.
values, vectors = np.linalg.eig(covariance_matrix)
print('\n Eigenvalues: \n',values)
print('\n Eigenvectors: \n',vactors)5️⃣ Normalized된 데이터를 고유벡터에 projection 시키기
분산을 가장 크게하는 축에 투영한다.
서로 직교하는 기저를 기준으로 데이텨를 변환한다!
Z = np.matmul(standardized_data, vectors)❗️ 차원축소를 하고자 PCA 과정을 거치면 결과값으로는 차원 축소가 된 결과가 나오지 않는다.
PCA는 고차원의 데이터를 분산을 유지하는 축(PC)을 기반으로 데이터를 변환한 것이며 해당 PC들 중 일부를 사용하는 것으로 차원축소를 할 수 있는 것이다. 즉, PCA는 고차원의 데이터를 분산을 유지하는 데이터의 축을 기반으로 데이터를 바꾼 것이고 위의 예시에서 PCA를 한 결과가 3차원이 나왔다면 최대 축을 3개를 사용할 수 있다는 것이다. 축은 데이터에 대해 몇 퍼센트 정도 설명하고 싶은가에 따라 선택하면 된다.
💻 sklearn 라이브러리를 사용해서 PCA하기
#1. 데이터셋 불러오기
import pandas as pd
import seaborn as sns
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
##1-1. 데이터셋의 일부를 사용하기 위해 전처리하기
penguins_raw = pd.DataFrame(sns.load_dataset('penguins'))
header = ['species', "bill_length_mm", "bill_depth_mm",
"flipper_length_mm","body_mass_g"]
numeric_header = header[1:]
penguins_df = penguins_raw.loc[:,header]
penguins_df = penguins_df.dropna().reset_index().drop('index', axis=1)
#2. 표준화
##2.1 위의 데이터셋의 일부는 카테고리형 데이터이고 일부는 연속형 데이터이므로 분류해주자.
numeric_data = penguins_df[numeric_header]
categorical_data = penguins_df['species']
##2.2 standard된 scaled data로 연속형 데이터 바꿔주기
std_penguin_df = pd.DataFrame(StandardScaler().fit_transform(numeric_data), columns=numeric_header)
# 3. PCA with scaled data
from sklearn.decomposition import PCA
pca = PCA(2) #4차원의 데이터를 2차원으로 줄인다.
pc_data = pca.fit_transform(std_penguin_df)
ratio = pca.explained_variance_ratio_
print("\n Eigenvectors: \n", pca.components_)
print("\n Eigenvalues: \n",pca.explained_variance_)
print("\n 2 variances ratio: \n", ratio)🍏(추가) matplotlib으로 시각화하기
색상을 따로 지정해야 species 별로 색상이 구분되는 결과값을 얻을 수 있다.
# 시각화를 위한 전처리(dataframe형으로 처리하기)
pc_penguin_df = pd.DataFrame(pc_data, columns=['PC1', 'PC2'])
pc_penguin_df = pd.concat([pc_penguin_df, penguins_df['species']], axis = 1) ## concate_by_column
pc_penguin_df
# Scatter plot with different colors by group
import matplotlib.pyplot as plt
##'species'끼리 묶어주기
groups = pc_penguin_df.groupby('species')
fig, ax = plt.subplots()
for name, group in groups:
ax.plot(group.PC1,
group.PC2,
marker='o',
linestyle='',
label=name)
ax.legend(fontsize=10, loc='lower right') # legend position
plt.xlabel('PC1')
plt.ylabel('PC2')
plt.show()🍏(추가) seaborn으로 시각화하기
hue를 species에 따라 자동으로 분류해준다는 점에서 좀 더 편리하다.
# 시각화를 위한 전처리(numpy로 처리 후 데이터프레임화하기)
pc_penguin_df = np.c_[pc_data, penguins_df['species']] # 넘파이로 두 배열(투사된 값과 종류)을 열로 붙이는 역할. concat과 비슷한 역할을 한다.
df_visualize = pd.DataFrame(pc_penguin_df, columns=['PC1', 'PC2','Species'])
sns.scatterplot(data=df_visualize, x='PC1', y = 'PC2', hue='Species'❗️ standardized data는 수동으로 구할 때와 라이브러리를 활용할 때와 다를 수 있다.
standard deviation에 쓰이는 자유도가 1이냐 혹은 0이냐에 따라 값은 달라질 수 있다. 유의미한 차이는 아니기 때문에 무시할 수 있다.
🍎(추가) PCA에서의 공분산
공분산 행렬은 '데이터의 구조(혹은 형태)'를 기술하는 수학적 방법이다.
공분산 행렬의 고유벡터는 데이터가 어떤 방향으로 분산되었는지 나타내준다.
🍎(추가) PCA에서의 고유벡터 (Eigenvector)와 고유값 (Eigenvalue)
새로운 축을 만들어 데이터를 변환하기 위해서 공분산의 고유벡터와 고유값을 구한다. 고유벡터와 고유값은 항상 쌍을 이룬다.
-
고유벡터: transformation에 영향을 받지 않는 회전축(혹은 벡터). 데이터를 변환 할 새로운 축이 된다.
-
고유값(): 고유벡터에 따라 '값이 얼마나 변하는가'를 의미하며, 데이터의 분산에 영향력이 큰 PC를 선택하기 위한 기준이 된다. 고유값이 큰 순서대로 고유 벡터를 정렬하면 결과적으로 중요한 순서대로 주성분을 볼 수 있다.
🍎(추가) 정규화(Normalization) vs 표준화(Standardization)
정규화와 표준화는 모두 feature들의 단위를 무시할 수 있도록 feature의 value들을 특정 범위로 나타낸다는 점에서 feature scaling이라고 한다.
- 정규화(Normalization)
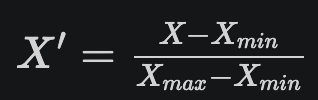
값들을 특정 범위, 주로 [0,1]이나 [-1,1]로 스케일링하는 것. 표준화를 포함하는 넓은 개념이다. 분산을 모를 때 유용하다.
- 표준화(Standardization)
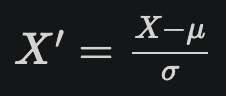
평균을 0, 표준편차를 1이 되도록 값을 스케일링(표준화)하는 것. 모집단의 분포가 정규분포나 가우시안 분포를 따를 때 유용하다.