Essence of Linear Algebra: vectors
위 영상의 한글판

벡터를 배우는 이유

선형대수학의 기초가 되기 때문이다.

벡터를 보는 세 가지 관점

• 물리학자: 공간상의 화살표. 한 벡터는 그 길이와 그것이 가리키는 방향으로써 정의된다. ~수적 해석 가능
• 컴퓨터 공학자: 숫자 자료를 배열한 것, 배열(리스트)의 자료구조로 나타내어진다. ~기하학적 해석 가능
• 수학자: 무엇이든 벡터가 될 수 있다. 스칼라곱이나 벡터합이 성립할 수 있으면 벡터다.

선형대수학 내에서 벡터의 덧셈과 상수배는 중요한 역할을 한다.

벡터(vector)

xy평면 같은 좌표계에 있는 꼬리가 원점에 고정되어 있는 화살표를 떠올리자.
공간에서 어떤 거리와 방향을 가진 발걸음이라고 할 수 있다.
선형대수학에서는 벡터가 원점에서 떨어지는 경우를 찾아보기가 어렵다.

점과 벡터 구분하기
점은 소괄호의 쌍으로 나타내고 벡터는 대괄호로 둘러쌓여서 나타낸다.
점: (x, y)
벡터: [x
y]

모든 벡터는 각각의 숫자 쌍과 일대일로 대응한다.

3차원에서는 z축을 추가하여 3연쌍으로 나타낸다.

벡터의 덧셈

벡터의 기초 연산 1

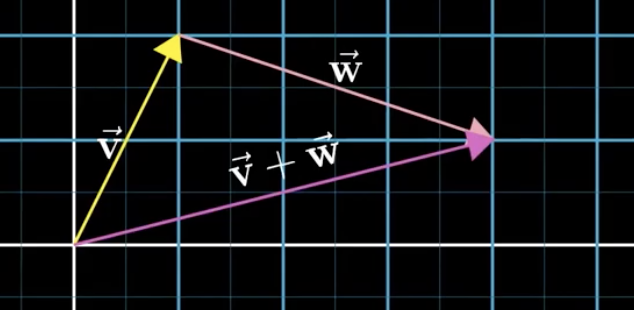
좌표계 위 벡터의 덧셈을 설명하는 가장 보편적인 방법으로 삼각형법이라고 불린다.

벡터의 곱셈 (상수배)

벡터의 기초 연산 2
상수에 의한 곱, 상수배.
상수를 벡터에 곱해주면 벡터는 처음 길이의 상수만큼 늘어나게 된다.
스케일: 벡터의 방향은 유지한 채 그 길이를 늘이고 줄이고 뒤집는 등의 과정
스칼라: 벡터의 곱셈에 사용되는 상수 ~ 숫자

데이터 사이언스에서 선형대수학

선형대수학은 데이터 분석가에게 많은 숫자의 배열을 시각적으로 개념화하기 좋은 방법을 제공한다. 데이터 속의 패턴을 설명하고 어떤 연산에 대한 보편적인 관점을 제공한다. 또한 수학이나 물리적인 관점에서 공간과 공간의 조작을 숫자를 사용해서 묘사하는 언어를 제공해서 컴퓨터에서 구현할 수 있도록 한다.