간단하게 표현하자면 벡터는 데이터를 1차원으로 표현하는 방식이고,
행렬은 데이터를 2차원으로 표현하는 방식이다.

🖤 스칼라

단일 숫자이며, 변수에 저장 할때는 일반적으로 소문자를 이용하여 표기한다.

• 스칼라와 벡터는 선형 대수를 구성하는 기본 단위이다.
• 스칼라는 크기, 벡터는 크기와 방향을 가지고 있다고 생각할 수 있다.
• 스칼라는 변수로 저장되어 있는 단순한 숫자이며 벡터 혹은 매트릭스에 곱해지는 경우 해당 값에 곱한 값으로 결정된다.
• 실수와 정수 모두 사용이 가능하다.

a = 5 , b = 1.81, c = -3.12e+23, d = 원주율

---

🖤 벡터

n차원의 벡터는 컴포넌트라 불리는 n개의 원소를 가지는 순서를 갖는 모음.
(컴포넌트는 스칼라로 간주 되지 않는다.)
즉, 숫자를 원소로 갖는 array.

• 벡터는 일반적으로 위의 화살표 (→) 를 갖는 소문자의 형태로 표현 됩니다. = $\vec{v}$

위의 벡터들은 각각 2, 3, 1, 4차원을 가지고 있다.

• 크게 보면 벡터의 길이(length)는 벡터의 차원수와 동일하다고 할 수 있다.
  위의 데이터에서 a의 길이는 2, b의 길이는 3, c의 길이는 1, d의 길이는 4인 것이다. 엄밀하게 말하면 의미가 다르지만 일단은 그렇게 알아두었다. 차원이 3이라는 것은 3차원 공간에 이 벡터를 그릴 수 있다는 것을 의미한다.

이러한 벡터를 파이썬으로 표현할 때는 numpy라이브러리의 np.array를 많이 활용한다. 왜냐하면 list나 np.array는 array 형식이라는 점에서 모양은 같지만 np.array를 쓰면 numpy 라이브러리가 가지고 있는 API를 사용할 수 있기 때문에 좀 더 간단하게 할 수 있기 때문이다!

#a와 b라는 리스트의 예.
a = [1,2]
b = [3,4]

#c와 d라는 np.array의 예.
c = np.array([5,6])
d = np.array([7,8])

• 데이터의 순서(order)가 바뀌면 다른 값이 된다.
• list라는 data structure(여기에서는 데이터를 담는 구조를 의미함)로 표현할 수 있다.

list 말고 데이터를 넣을 수 있는 것 중에 순서가 상관없는 것으로 Set 이라는 것도 있다.

🤍 Norm, Magnitude, length

💡Norm

벡터의 크기(magnitude) 또는 길이(length)를 측정하는 방법을 의미한다.

• 두 벡터 사이의 거리: 벡터의 뺄셈으로 계산
• 두 벡터 사이의 각도: 놂 2로만 계산

𝐿1 Norm

변화량의 절대값을 모두 더한다. (삼각형의 밑변, 높이)
|𝑣|=|𝑥0|+|𝑥1|+...+|𝑥𝑛|

기하학적 성질은 마름모 → Robust 학습, Lasso회귀에 활용

𝐿2 Norm

변화량의 절대값을 모두 더한다 (삼각형의 밑변, 높이)
$||v|| = \sqrt {{x_0}^2 + {x_1}^2 + ... + {x_n}^2}$

기하학적 성질은 원 → Laplace 근사, Ridge 회귀에 활용
두 벡터 사이의 각도를 구할 때: 두 벡터 array의 내적(np.inner(x ,y))사용. inner(x, y)를 사용하는 이유는 머신러닝에서 두 데이터 혹은 패턴의 유사도를 측정하기 때문이다. 각도는 제2코사인 법칙으로도 구할 수 있다. 바로 역코사인(arc cos)값으로 구할 수 있는 것이다.(np.across(x,y))

import numpy as np
# L1 놂
def l1_norm(x):
    res = np.abs(x)
    res = np.sum(x_norm)
    return res

# L1 놂 한 줄로 표현하기
L1 = np.sum(np.abs(v))    

# L2 놂
def l2_norm(x):
    res = x **2
    res = np.sup(res)
    res = np.sqrt(res)
    return res

#L2 놂 한 줄로 표현하기 
L2 = np.sqrt(np.sum(v**2))
    
# np.linalg.norm 으로도 구현 가능하다!
import numpy as np
from numpy import linalg
## v = np.array()
L1 = linalg.norm(v,ord=1)
L2 = linalg.norm(v,ord=2)

💡Magnitude(크기)

v라는 벡터의 크기는 다음과 같이 표현할 수 있다. = $| v |$
(절댓값같이 생겼지만 절댓값이 아니다!)

v = [1,2,3,4]
|v| = $\sqrt{ 1^2 + 2^2 + 3^2 + 4^2 }$
|v| = 30

벡터의 크기는 모든 원소의 제곱을 더한 후 루트를 씌운 값이다.

벡터의 크기의 특징

• ||𝑥||≥0
• ||𝑥||=0 (모든 원소가 0)
• 삼각 부등식: ||𝑥+𝑦||≤||𝑥||+||𝑦||

💡Length (길이)

엄밀한 의미에서 차원과 길이는 다르지만, 일단 차원과 비슷하다고 하자.

벡터의 내적 (Dot Product)

두 벡터 𝑎⃗ 와 𝑏⃗ 의 내적은, 각 구성요소를 곱한 뒤 합한 값과 같다.
v = [1, 2, 3, 4]
x = [5, 6, 7, 8]
v ⋅ x = 1 5 + 2 6 + 3 7 + 4 8 = 70

벡터의 내적을 위해서는 쌍끼리 순서를 맞춰서 곱하고 더하려면 쌍이 있어야 하기 때문에 두 벡터의 길이가 반드시 동일해야 한다.

---

🖤 행렬(=Matrics = array)

데이터를 2차원으로 표현하는 방식이다. 고등학생 때 행렬을 배운 세대여서 그런가 많이 익숙하지만 데이터 사이언스에 있어서 행렬은 위의 벡터가 여러 개로 이루어진 데이터의 집합이라고 할 수 있다.

행렬(매트릭스)란, 행과 열을 통해 배치되어있는 숫자들이다. 매트릭스를 표현하는 변수는 일반적으로 대문자를 사용하여 표기한다.

가로줄을 행이라고 하고 세로줄을 열이라고 한다.
차원을 표기 할때는 행을 먼저, 열을 나중에 표기한다. (그래서 행-열이다.)
행렬은 array를 묶어서 표현하거나 pandas의 dataframe으로 표현할 수 있다.

#pandas dataframe으로 표현
import pandas as pd
df = pd.DataFrame([
              [89, 90, 85, 87],
              [80, 84, 85, 85]
], index = ['studentA', 'studentB'], columns = ['mid1', 'mid2', 'mid3', 'final'])

#np.array로 표현
d = np.array([[89, 90, 85, 87],
              [80, 84, 85, 85]])

np.array로 표현할 때 한 줄로 보이는 것이 한 열이라고 보면 된다.
np.matrix라는 함수도 있지만 이 함수는 없어질 예정이라고 하니 np.array를 적극적으로 사용하자.

매트릭스의 행과 열의 숫자를 차원 (dimension, 차원수 등)이라 표현한다.

🤍 Determinant(행렬식)

🤍 Matrix multiplication(행렬의 곱셈)

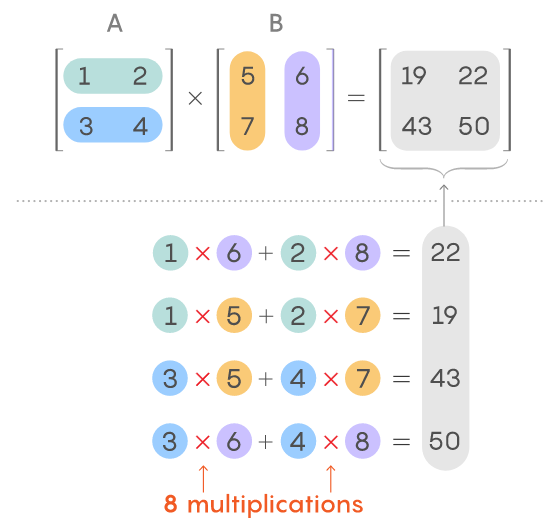
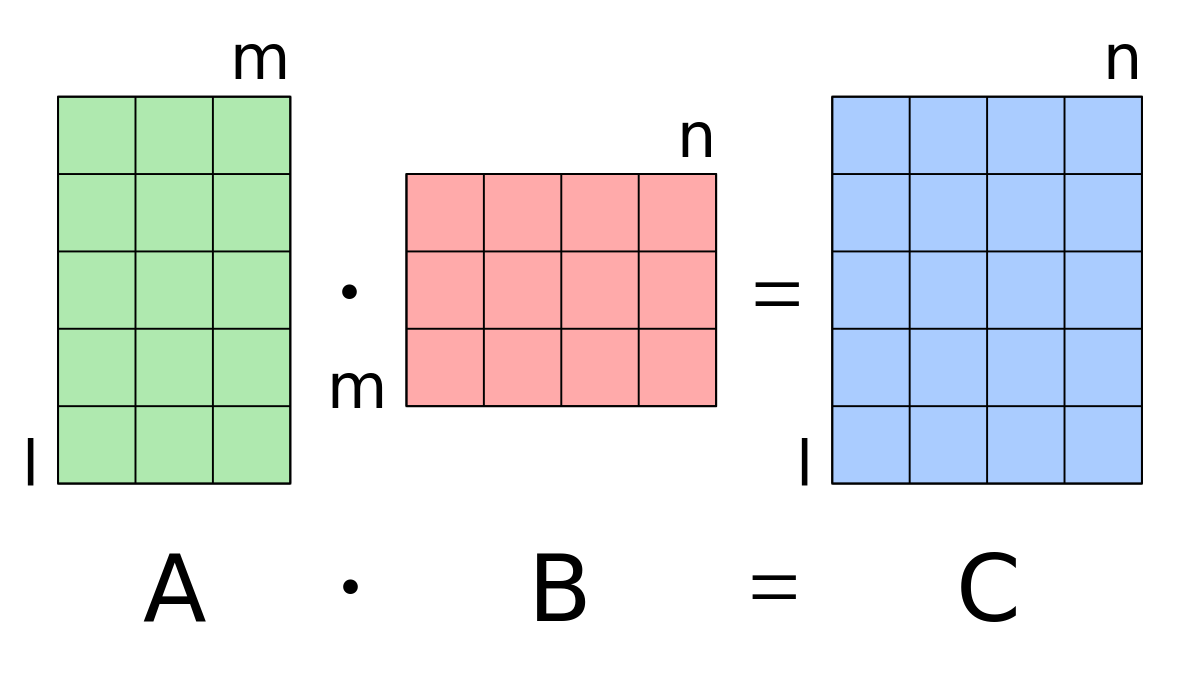
앞의 행렬의 행과 뒤의 행렬의 열의 각 요소를 차례대로 곱해준 뒤 그 합을 결과값을 넣을 행렬에 넣는다.

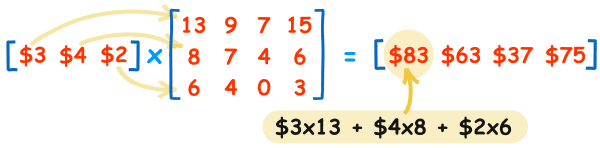
🤍 Transpose (행렬의 전치)

매트릭스의 전치는, 행과 열을 바꾸는 것을 의미한다.
일반적으로 매트릭스 우측 상단에 𝑇 혹은 tick(`)마크를 통해 표기된다.
대각선 부분의 구성요소를 고정시키고 이를 기준으로 나머지 구성요소들을 뒤집은 형태이다.

🤍 Square matrix(정사각행렬)

정사각 매트릭스는, 정방 매트릭스라고도 불린다.
행과 열의 수가 동일한 매트릭스이다.

정사각 행렬의 특별한 케이스

• Diagonal (대각): 대각선 부분에만 값이 있고, 나머지는 전부 0인 것.
  
• Upper Triangular (상삼각): 대각선 위쪽 부분에만 값이 있고, 나머지는 전부 0인 것.
  
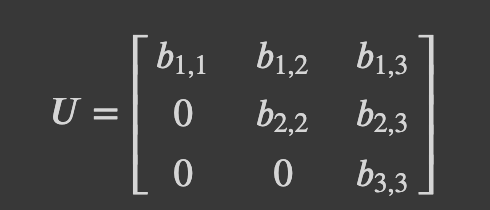
• Lower Triangular (하삼각): upper triangular 와 반대로, 대각선 아래에만 값이 있는 것.
  
• ⭐️ Identity (단위 매트릭스) ⭐️:
  Diagonal 매트릭스 중에서, 대각선의 값이 1인 경우이다.
  임의의 정사각 매트릭스에 단위 행렬을 곱하면, 그 결과값은 원본 정사각 매트릭스로 나오며, 반대로 임의의 매트릭스에 대해서 곱했을때 단위 매트릭스가 나오게 하는 매트릭스를 역행렬 (Inverse)라고 부른다.
  $AI == A$
  $AA^{-1} = I$
  
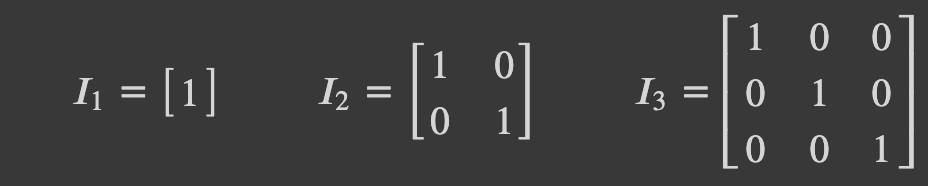
• Symmetric (대칭): 대각선을 기준으로 위 아래의 값이 대칭인 경우 입니다.
  

💛 Determinant(행렬식)

역행렬의 존재 여부를 판단할 수 있다. (0이면 역행렬이 존재하지 않음)
행렬을 하나의 '스칼라'값으로 표현하는 방법.

행렬식은 모든 정사각 매트릭스가 갖는 속성으로, 𝑑𝑒𝑡(𝐴) 혹은 |𝐴| 로 표기한다. 행렬식을 사용하는 목적은 데이터의 특성을 알아보기 위함이다. determinant는 데이터의 속성을 숫자 하나로 압축해서 표현하는 것이라고 할 수 있다.

2x2 행렬의 행렬식은 $ad-bc$
3x3 행렬의 행렬식은 아래와 같다.

#np.linalg.det() 메서드로 구할 수 있다.

import numpy as np
from numpy import linalg

#m = np.array()
det = np.linalg.det(m)

❗️❗️행렬식이 0인 경우 (determinant가 0, 역행렬이 없는 경우) = "특이" (singular) 매트릭스❗️❗️

행렬식이 0인 정사각 매트릭스는 "특이" (singular) 매트릭스라고 불리기도 한다. 이들은 2개의 행 혹은 열이 선형의 관계를 (M[,i]= M[,j] x N) 이루고 있을때 발생한다. (M[,i]= M[,j] x N)의 형태는 아래와 같은 형식이다.

이를 표현하는 다른 방법은, 매트릭스의 행과 열이 선형의 의존 관계가 있는 경우 매트릭스의 행렬식은 0이다. 라고 표현하는 것이다.(행과 열이 일정하게 커지는 관계이면 행렬식은 0이라고 할 수 있는 것. 행으로는 2배씩, 열로는 3배씩 커지는 선형의 의존관계가 있다.)

---

추가 공부

💎 행렬의 곱(multiplication) vs 행렬의 내적(dot product)

행렬의 곱(multiplication)
$m * n$ 행렬과 $n * p$ 행렬을 곱해주면 $m * p$ 행렬이 나온다.

import numpy as np

np.matmul(A,B)

행렬의 내적(dot product)
두 행렬의 같은 위치에 있는 요소들끼리 곱해서 더한 값이다.

import numpy as np

np.dot(A,B)

💎 역행렬 python으로 구하기

import numpy as np
from numpy import linalg
#m = np.array()
np.linalg.inv(m)

#역행렬이 없는 경우 -1이 출력되도록 하는 사용자 지정 함수
def myInverse(m):
  try:
    inverse = np.linalg.inv(m)
    return inverse
  except:
    return -1

💎 내적의 의미 (보충자료 필요)

내적은 정사영된 벡터 길이와 관련이 있다.
(주의: 프로그래밍(행렬)의 내적과 수학의 내적은 다르다!)

내적은 정사영의 길이를 ||y||만큼 조정한 값으로, 정사영된 벡터의 길이와 관련이 있다. inner<x,y>를 통해 구할 수가 있는데 머신러닝에서 이를 활용하여 두 데이터 혹은 두 패턴이 얼마나 유사한지 파악할 수 있다.

💎 Cramer's rule

크레머의 공식을 잘 설명한 블로그
크레머의 공식을 이용해서 문제를 푸는 과정
조건: AX = B이며 B가 0행렬이 아니고, det(A)가 0이 아니다.
(A는 미지수 앞의 값의 행렬, X는 구하고자하는 미지수의 행렬, B는 AX의 결과값에 대한 행렬이라고 할 수 있다.)

문제 풀이 과정도 정석과 쉽게 푸는 방법 두 가지를 모두 써보았다.

💎 series vs numpy.array vs list

• series : 데이터프레임의 구성요소. 행렬의 벡터같은 요소이다. 1차원의 데이터만 다룰 수 있다.
• np.array : 다차원의 데이터를 다룰 수 있는 틀로 이를 묶으면 행렬도 되고 데이터프레임과 같은 형식으로도 만들 수 있다.
• list : 파이썬에서 자주 활용되는 데이터를 담는 방식이지만 리스트를 가공할만한 특성이나 도구가 array보다 적기 때문에 array를 많이 쓴다.
  list vs array