선형회귀모델(Linear Regression Model)

종속변수(y)의 변동을 독립변수(x)로 설명하는 것.

머신 러닝의 가장 큰 목적은 실제 데이터를 바탕으로 모델을 생성해서 미래의 결과값을 예측하는 데에 있다고 할 수 있다. 즉, 임의의 입력값을 넣었을 때 발생할 아웃풋을 예측하는 모델 중 하나가 선형회귀모델이다.

관계식 중 가장 직관적이고 간단한 모델은 선(line)이다. 어떤 데이터를 가장 잘 설명할 수 있는 선을 찾아 이를 분석하는 방법을 선형 회귀(Linear Regression) 분석이라고 한다.

회귀에 의한 변동($\beta_1$)와 y 절편($\beta_0$)으로 이루어진 직선의 식으로 표현할 수 있다.
$y$ = $\beta_1$$x$ + $\beta_0$

🍏 회귀(regression)란, 통계학에서 관찰된 연속형 변수들에 대해 두 변수 사이의 모형을 구한뒤 적합도를 측정해 내는 분석 방법이다.

🍏 회귀분석은 시간에 따라 변화하는 데이터나 어떤 영향, 가설적 실험, 인과 관계의 모델링등의 통계적 예측에 이용될 수 있다. 회귀분석은 어떤 변수가 다른 변수에 의하여 설명된다고 보고 그 함수 관계를 조사하는 통계적인 해석 기법이다.

🍏 하나의 종속변수와 하나의 독립변수 사이의 관계를 분석할 경우를 단순회귀분석(simple regression analysis), 하나의 종속변수와 여러 독립변수 사이의 관계를 규명하고자 할 경우를 다중회귀분석(multiple regression analysis)이라고 한다.

실제값 : $y = \beta_0 + \beta_1 x_1 + \varepsilon_i$
예측값 : $\hat y = \hat\beta_0 + \hat\beta_1 x_1$

⭐️ 최소제곱법(Least Square Method)

선형회귀모델을 잘 만들었다는 말은 실제값과 예측값의 차이, 즉, 오차(error)가 적다는 의미이다. 이는 $\varepsilon_i$가 작을수록 예측을 잘했다는 의미가 되기도 할 것이다.

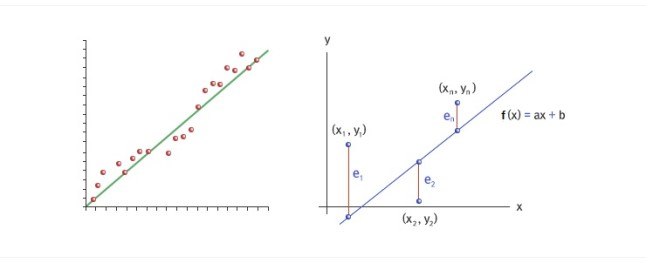
선형 회귀 모델의 목표는 모든 데이터로부터 나타나는 오차의 평균을 최소화할 수 있는 최적의 기울기와 절편을 찾는 것이라고 할 수 있다.

오른쪽 그림에서 자료 ($x_1$,$y_1$), … , ($x_n$, $y_n$)를 가장 잘 설명할 수 있는 직선 방정식이 $f(x)=ax+b$이라면, 각 점 $x_i$의 좌표값$y_i$와 함수값$f(x_i)$의 오차$y_i-f(x_i) = y_i-(ax_i+b)$의 제곱의 합이 최소가 되는 경우이다. 즉, 다음 식이 최소가 되는 경우이다.

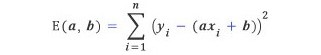
이러한 식을 최적의 최소 제곱직선이라고 부르는데, E(a, b)의 최솟값은 a와 b에 의해 결정되므로 직선의 기울기 a와 절편 b의 값을 찾는 것이 열쇠가 된다. E(a, b)의 최솟값은은 편미분을 했을 때 편미분 ∂E/∂a와 ∂E/∂b가 0이 되어야 한다.

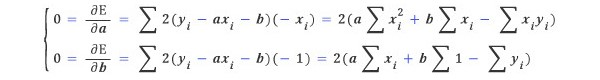
이 연립방정식을 활용해서 풀면 기울기인 a와 y 절편인 b에 대한 식을 구할 수 있다.


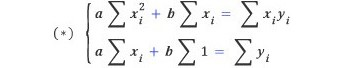
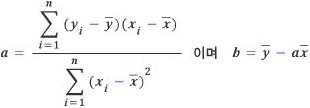
$y^-$는 $y_i$의 평균, $x^-$는 $x_i$의 평균을 의미한다.
$a$에 관한 식을 좀 더 잘 이해할 수 있게 풀어서 서술한 게 아래의 식이다. 즉, 점 ($x_1,y_1$)과 점 ($x_2,y_2$)를 지나는 선의 기울기가 $a$인 것이다.

지도학습(Supervised Learning)

회귀분석과 분류의 타겟 특성은 무엇이 다른가?

회귀(Regression)

How much? How many?

분류(Classification)

Is this A or B?

기준모델(Basic Line Model)

예측 모델을 구체적으로 만들기 전에 가장 간단하고 직관적이면서 최소한의 성능을 나타내는 기준이 되는 모델. 평균값을 기준 모델로 많이 사용한다. 하지만 기준모델은 평균값이 아니다.

기준모델 설정

• 분류문제의 기준모델: 타겟의 최빈 클래스
• 회귀문제의 기준모델: 타겟의 평균값
• 시계열회귀문제: 이전 타임스탬프의 값

Scikit-learn을 이용해 선형 회귀 모델을 만들어 사용하고 해석하기

• sklearn을 사용하기 위해서는 pandas의 데이터 프레임에서 matrix 형태로 바꿔줘야 수학적 계산이 가능하다.

• '머신러닝 = 아주 고도화된 계산기'로 생각하면 쉽다. input의 형태가 matrix여야한다.
  

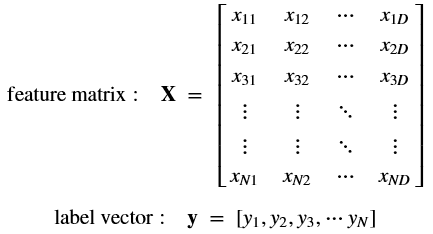
• 특성행렬은 주로 $X$ 로 표현하고 보통 2차원 행렬([n_samples, n_features])

  → 주로 NumPy 행렬이나 Pandas 데이터프레임으로 표현

• 타겟배열은 주로 $y$로 표현하고 보통 1차원 형태(n_samples)

  → 주로 Numpy 배열이나 Pandas Series로 표현

위키피디아 '회귀'
최소제곱법 네이버 지식백과