⭐️ 정규화(regularization)

정규화(Regulatrization) : 회귀모델에서의 정규화란 모델을 변형하여 과적합을 완화해 일반화 성능을 높여주기 위한 기법을 말한다.
정규화의 강도를 조절해주는 패널티 값인 람다(lambda, $\lambda$)는 다음과 같은 성질을 가지고 있다.

• $\lambda$ → 0 이라면 $\beta_{ridge}$ → $\beta_{OLS}$
• $\lambda$ → $\infin$ 이라면 $\beta_{ridge}$ → 0
  식을 확인한다면 어떤 의미인지 더 확실하게 와닿을 것이다.

Ridge regression와 Lasso regression를 이해하려면 일단 정규화(regularization)를 이해해야한다.

위의 세 모델 중 왼쪽의 과소적합된 모델과 오른쪽의 과적합된 모델을 먼저 살펴보자.

underfitted 또는 high bias된 모델은 bias가 큰 모델이다. test data를 위한 학습이 덜 된 것이 원인이고, 이는 train data와 test data간의 차이가 너무 커서 train data로만 학습한 모델은 test data를 맞출수가 없는 것을 의미한다.

overfitted 또는 high variance된 모델은 variance가 큰 모델이다. 현재 데이터로는 잘 맞겠지만 다른 데이터를 사용한다면 정확한 예측을 하지 못한다. 이런 variance가 큰 모델은 train data에 over-fitting된 것이 원인이고, 이는 너무 train data에 fitting된 모델을 만들어서 test data에서 오차가 심하게 발생한 것을 의미한다.

가운데에 있는 모델은 어느정도 데이터에 적합하면서 bias와 variance에 대해서도 적절하기 때문에 셋 중 가장 적합한 모델이라고 할 수 있다.

bias와 variance에 대한 추가자료

이렇게 모델을 만들 때, bias와 variance를 둘 다 줄여주면 제일 좋겠지만 하나를 포기해야 하는 경우가 발생한다. cost, 즉 시간과 비용문제나 효율성의 측면에서 한쪽을 줄이는 것을 포기하는 것이 바람직할 수 있는 것이다. 이 때 bias를 가지더라도 제일 작은 variance를 가지는 모델을 만드는 것도 좋지않을까?라고 생각해볼 수 있다. 즉, overfitting을 해결함으로써 효과를 볼 수 있지 않을 수 있다는 것에서 시작할 수 있다.

overfitting을 해결하는 방법은 크게 두 가지가 있다.

1. 특성(Feature)의 갯수를 줄이기

• 주요 특징을 직접 선택하고 나머지는 버린다.
• Model selection algorithm을 사용한다.

2. 정규화(Regularization)를 수행한다.

• 모든 특성을 사용하되, 파라미터(세타)의 값을 줄인다.

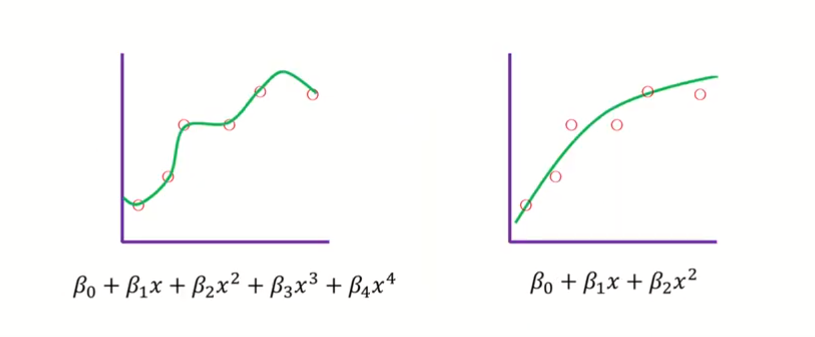
왼쪽의 모델은 overfitting된 모델이다. 이 모델을 오른쪽 모델처럼 바꿔주는 것이 정규화 과정이다. 전체식이 최소화되게 해주려면 $\beta_3$과 $\beta_4$가 0이 되어주는 것이라고 할 수 있다. 이처럼 베타값(파라미터값)에 제약을 줌으로써 모델을 정돈을 주는 것이 정규화이다. 정규화를 통해서 모델은 일반성을 확보할 수 있게 된다.

위의 (1)은 linear regression cost function이고 베타는 coefficient size이다. 위의 그림에서 (1)Training accuray만 있으면 최소제곱법(OLS)과 다른게 없는데 (2)Generalization accuaracy가 추가되면서 베타에 제약을 줄 수 있어 정규화를 할 수 있다. 이렇게 계수 추정치를 줄여주는 정규화 방법을 shrinkage method라고 표현하기도 한다.

이런 정규화(Regulization) 컨셉을 처음 도입한 모델이 Ridge Regression인 것이다. Ridge Regression과 같은 경계화 모델은 편향 에러를 더 더하는 대신 모델의 분산을 줄이는 방법으로 일반화를 유도하는 방법이다.

정규화(regulation)을 위한 회귀모델

정규화(regularized) 선형회귀 방법은 선형회귀 계수(weight)에 대한 제약 조건을 추가함으로써 모형이 과도하게 최적화되는 현상인 과적합을 막는 방법이다. 정규화를 위한 선형회귀방법을 Regularized Method, Penalized Method, Contrained Least Squares 이라고도 불리운다.

모형이 과도하게 최적화되면 모형 계수의 크기도 과도하게 증가하는 경향이 나타난다. 이를 방지하기 위해 정규화 방법에서 추가하는 제약 조건은 일반적으로 계수의 크기를 제한하는 방법이다. 일반적으로 다음과 같은 세가지 방법이 사용된다.

• Ridge 회귀모형
• Lasso 회귀모형
• Elastic Net 회귀모형

⭐️ Ridge Regression(릿지 회귀, L2)

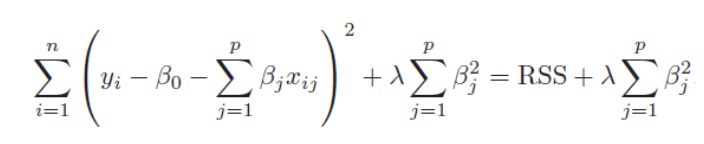
릿지 회귀는 기존 다중회귀선을 훈련데이터에 덜 적합하도록 만들어서 더 좋은 모델이 만들어지도록 하는 것이다. 과적합을 줄이기 위해서사용되는 회귀방법으로 모델의 복잡도를 줄이는 방법을 사용하는데 feature의 수를 줄이거나 모델을 단순한 모양으로 적합하는 것이다.

다중공선성 문제와 over-fitting 과적합 문제 방지를 위해 L2 정규화가 사용되었다.

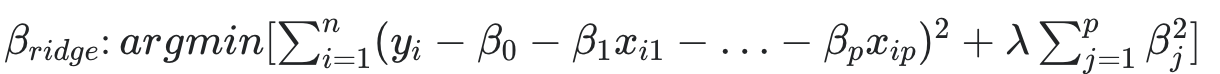
n = 샘플의 수, p = feature의 수, $\lambda$ = 튜닝 파라미터(패널티)
여기에서 alpha, lamda, regularization parameter, penalty term은 모두 같은 뜻이다.

릿지 회귀는 편향(bias)를 조금 더하고, 분산(variance)를 줄이는 방법으로 정규화(regulation)을 수행한다.

alpha = lamda = regularization parameter =penalty term

alpha값 즉 람다 값에 따른 기울기의 변화를 살펴보면, 람다값이 커질수록 회귀계수의 값은 0에 가까워 지고 기울기는 평균기준모델에 가까워진다.

람다는 값이 커질수록 회귀계수들을 0으로 수렴(기울기를 평균과 비슷하게)시키며 이것은 덜 중요한 특성의 개수를 줄이는 효과(과적합을 줄이는 효과)를 보여준다.

람다가 0에 가까워 질수록 다중회귀모델에 가까워지게 되기 때문에 적절한 람다값을 구하는 것이 일반화가 잘되는 지점을 찾는 것이라고 할 수 있으며 이것을 정규화 모델이라고 부른다.

구하는 방법: 교차검증(cross-validation)

최적의 알파값을 찾는 특별한 공식을 사용하는 것이 아니라 여러 패널티 값을 가지고 검증실험을 하는 것이다. 즉 교차검증(cross-validation)을 사용해 훈련/검증 데이터를 나누어 검증실험을 하여 가장 적절한 알파값, 즉 람다를 찾는 것이다.

sklearn에서 내장된 교차검증 알고리즘을 적용하는 RidgeCV를 통해서 최적의 패널티(alpha,람다)를 검증할 수 있다.

from sklearn.linear_model import RidgeCV

alphas = [0.01, 0.05, 0.1, 0.2, 1.0, 10.0, 100.0]

ridge = RidgeCV(alphas=alphas, normalize=True, cv=3)
ridge.fit(ans[['x']], ans['y'])
print("alpha: ", ridge.alpha_)
print("best score: ", ridge.best_score_)

best_score_는 모델이 훈련 데이터에서 수행한 교차검증의 평균 정확도가 저장된 결과를 보여준다.
.

⭐️ Ridge 회귀를 통한 특성선택(Feature Selection)과정

특성공학(feature engineering)

과제에 적합한 특성을 만들어 내는 과정이라고 할 수 있다.
이 프로세스는 실무 현장에서 가장 많은 시간이 소요되는 작업 중 하나이다.

Feature Engineering is a process of using domain knowledge to extract features (characteristics, properties, attributes) from raw data. 위키피디아
< Feature Engineering의 절차>
1) Brainstorming or testing features →
2) Deciding what features to create →
3) Creating features →
4) Testing the impact of the identified features on the task →
5) Improving your features if needed →
6) Repeat →

릿지 회귀,라쏘회귀, 정규화 자료