시계열 데이터

yuns_u·2021년 10월 8일

시계열 데이터(time series)

가장 대표적인 시계열 데이터는 주식 데이터이다.
1년 코스피 지수 그래프는 365개의 코스피 지수가 모여서 만들어진 그래프이다.
이처럼 시계열 데이터는 일정 시간 간격으로 한 줄로 배열된 데이터를 의미한다고 할 수 있다.

일정 시간 간격으로 배열되어 있는 데이터인 시계열 데이터를 분석하기 전에 시계열을 구성하는 요소들을 살펴보고자 한다.

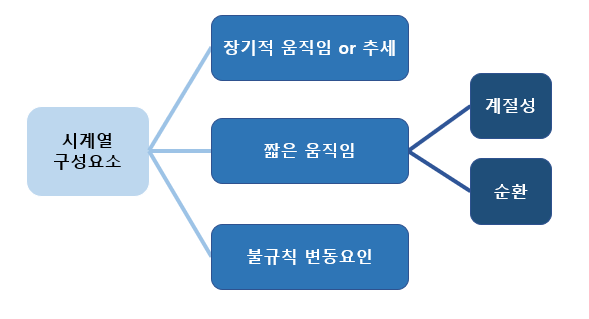
시계열 구성요소

시계열을 구성하는 4가지 요인은 아래와 같다.

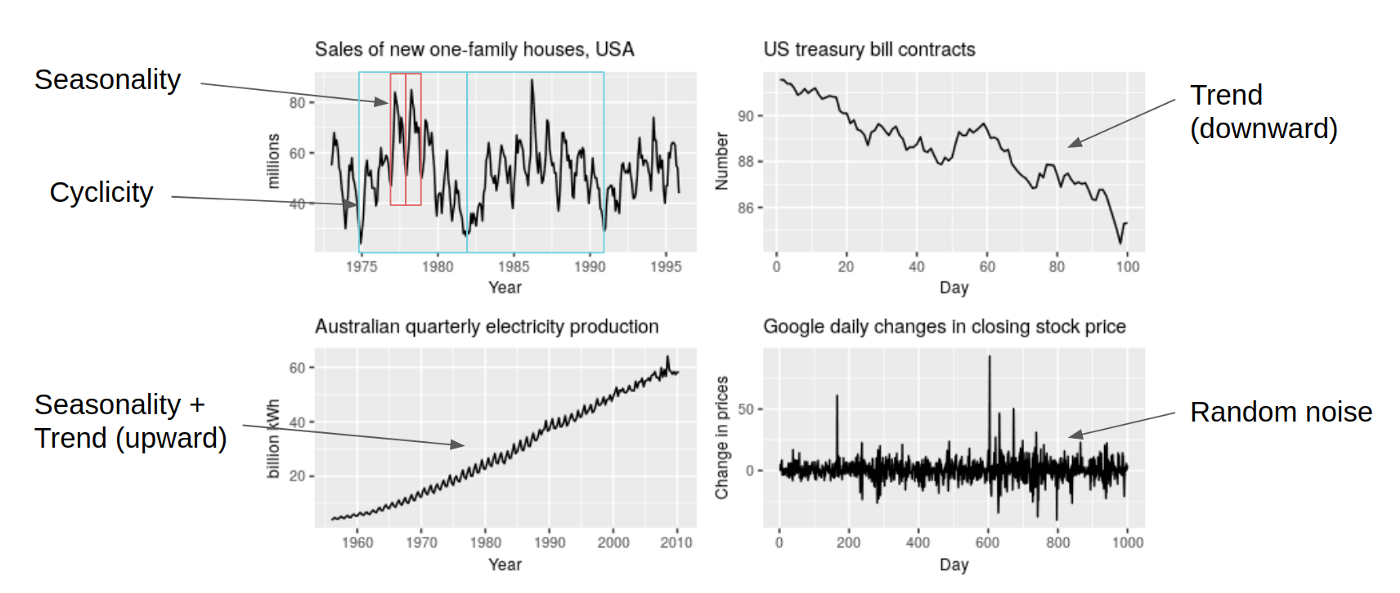
추세(trend)
추세는 장기간 데이터의 일반적인 경향을 보여준다.
부드럽고 일반적인, 장기적인 경향으로 전체적인 추세는 상향, 하향, 혹은 안정적이어야 한다.
짧은 구간에서는 다른 변동을 보여줄 수 있다.
인구, 농업 생산, 제조 품목, 출생 및 사망자 수, 산업 또는 공장 수, 학교 또는 대학 수는 일종의 추세를 보여준다.
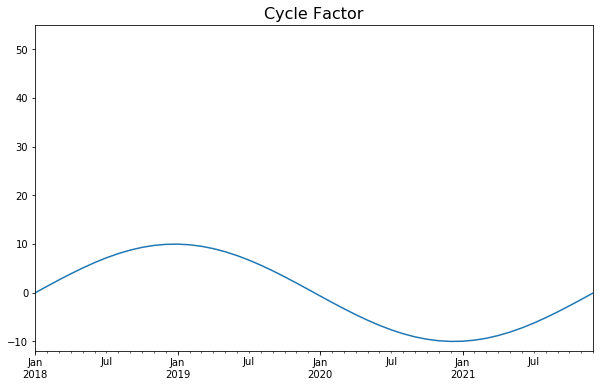
순환(cycle variation)
1년 이상 지속되는 시계열의 변동을 순환이라고 한다.
이 변동은 1년 이상의 주기를 가지며 Business Cycle이라고 불리기도 한다.

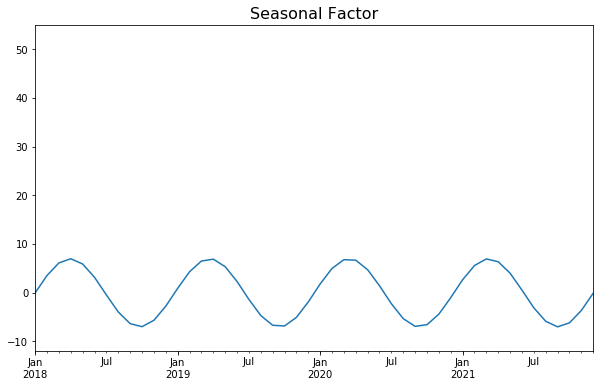
-계절성(seasonal variation)
1년 미만의 기간에 걸쳐 규칙적이고 주기적으로 나타나는 변동이다. 이러한 변동은 자연의 힘이나 사람이 만든 관습으로 인해 시작된다. 다양한 계절 또는 기후 조건은 계절 변화에 중요한 역할을 한다.
농작물 생산량은 계절에 따라 달라지고 여름에는 냉방기기 판매량이 높아지고 겨울에는 냉방기기 판매량이 낮아지는 특징을 보이는 것을 계절성이라고 한다.

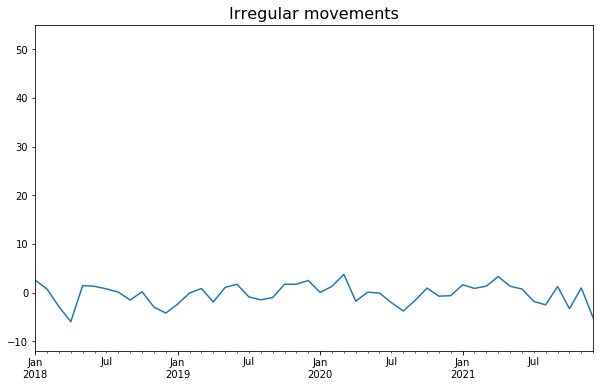
-불규칙 변동요인(random or irregular movements)
이 변동은 예측할 수 없고 제어할 수 없고 불규칙하다.

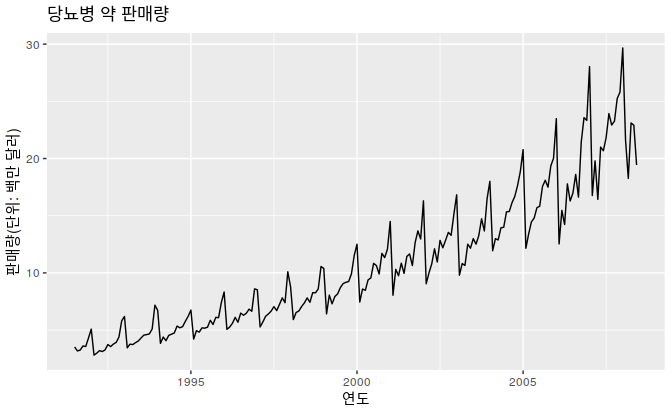
시계열 데이터 예시

시계열 구성요소 간의 구성(composition)

시계열 데이터를 구성하는 4가지 구성요소는 단일로 시계열을 구성할 수도 있고 가법, 승법또한 가능하다.

가법 모형(addictive model): 구성요소 간 독립적이라고 가정하여 각 구성요소를 더하는 모형
승법 모형(multiplicative model): 구성요소 간 독립적이지 않고 상호작용한다고 가정하여 구성요소 간 곱해주는 모형

여러 구성요소가 하나의 시계열 모형으로 있는 것을 여러 개로 나누는 것을 시계열 분해(de-composition)이라고 한다.

시계열 분석

시계열 데이터는 머신러닝 분야에서 자주 채택되는 영역이다.
실제 세상에는 시간적 요소가 중요한 케이스가 많기 대문에 시간적 요소가 중요한 데이터가 많은 것이다.
시계열 데이터는 시간 변수와 한 개 혹은 여러 개의 변수들로 구성되어 있다.
시간과 한 개의 변수로 데이터가 구성되어 있을 때는 분석이 비교적 쉽다.
하지만 여러 개의 변수로 데이터가 구성되어 있으면 분석이 어렵다.
시계열 데이터가 아닌 데이터에 대한 다변수 분석과 비교해보았을 때 다변수 시계열 데이터는 분석이 더 어렵다고 한다.

단변량 시계열 데이터를 예측하는 방법으로는 머신러닝이나 딥러닝 방법보다는 전통적인 ARIMA, ETS 방법이 효과적이라고 한다.

시계열 데이터의 특성

시계열 데이터는 크게 규칙성을 가지는 패턴과 불규칙한 패턴을 가진 것으로 2가지로 나눌 수 있다.
규칙성을 가지는 패턴을 자기상관성(autocorrelativeness)과 이동평균현상(moving avergate)으로 나누어볼 수 있다.

자기상관성(autocorrelativeness): 이전의 결과와 이후의 결과 사이에서 발생하는 상관성
이동평균현상(moving avergate): 이전에 생긴 불규칙한 사건이 이후의 결과에 편향성을 초래하는 현상

불규칙한 패턴의 경우 일반적으로 white noise라고 칭하며 평균이 0이며 일정한 분산을 가진 정규분포에서 추출된 임의의 수치라고 가정하고 있다.

시계열은 추세 및 계절성 성분을 가지고 있으며 시계열 분석 시에는 이를 정상 과정 신호와 분리할 필요가 있다.
회귀 분석을 사용하여 이러한 성분을 분리하는 방법을 설명할 수 있다.

정상 과정(stationary process)은 시간이 지나도 신호의 확률ㅈ거 특성이 그대로 유지되는 확률 과정을 의미한다.
대부분의 시계열 분석은 정상 과정 분석 방법을 기반으로 한다.
정상 과정 모형 중 가장 대표적인 모형으로는 백색 잡음(white noise)과 ARMA(auto-regressive moving average) 모형이 있다.

비정상 과정(nonstationary process)은 시간에 지나면서 기댓값의 수준이나 분산이 커지는 등 시계열의 특성이 변화하는 확률 과정을 나타낸다.
비정상 과정 모형 중 가장 대표적인 것은 ARIMA(auto-regressive moving average) 모형이 있다.
ARIMA 모형외에도 ADF 검정 등의 단위근 검정(unit root test)를 사용하여 모형의 적분 차수(integration order)를 결정하는 법 등이 있다.

불규칙성을 띄는 시계열 데이터에 규칙성을 부여하는 방법으로 AR, MA, ARMA, ARIMA 모델 등을 이용하여 미래를 예측하는 방법이 일반적이었는데 이 방ㅌ법들은 선형 통계적인 방법이다.

시계열 데이터의 머신러닝 모델

머신러닝 방식과 전통적인 통계적 방법의 목표는 모두 Sum of sqaured error와 같은 손실 함수(loss function)를 최소화하여 예측 정확도를 향상시키는 것이 목표이다.
전통적인 통계적 방법은 선형 처리를 하지만 머신러닝 방법은 비선형 알고리즘을 사용하여 손실함수를 최소화하여 목표를 달성한다.
최근에는 딥러닝을 이용하여 시계열 데이터의 연속성을 찾아내는 방법이 연구되고 있다.
이 때에는 RNN 종류의 LSTM이 좋은 성능을 내고 있다고 한다.

머신러닝 알고리즘과 세부적인 딥러닝 알고리즘 목록은 아래와 같다.