큰 수의 법칙 ( 대수의 법칙, Law of large numbers )

sample 데이터의 수가 커질수록, sample의 통계치는 점점 모집단의 모수와 같아진다.

표본의 데이터의 수(사이즈)가 커질수록 표본의 통계치는 모집단의 통계치와 비슷해진다는 뜻이다.

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd

population = np.random.normal(50, 10, 1000) 
#mu = 50, sd = 10, number = 1000
population.var() 
#분산은 sd**2이니까 모집단의 분산은 100정도가 될 것이다.

여기에서 구한 population은 평균이 50, 표준편차가 10, 전체 데이터의 수가 1000인 모집단을무 무작위로 뽑은 것이다. 이 population의 표준편차가 10이므로 분산은 100에 가깝게 나올 것이다.

102.75193333162638

np.random.normal 함수 참조

이 population이라는 모집단에서 표본을 뽑아서 큰 수의 법칙을 증명해보자.
이 때 사용할 수 있는 함수는 np.random.choice(모집단, size)이다.

np.random.choice 함수 참조

np.random.choice(population, 5).var()
>>>104.809204061985

np.random.choice(population, 15).var()
>>>91.2005773156378

np.random.choice(population, 100).var()
>>>87.39613699882166

np.random.choice(population, 200).var()
>>>88.64058914194142

표본의 크기가 커질수록 표본의 분산이 모수에 점점 더 가까이 다가가는 것을 확인할 수 있다.

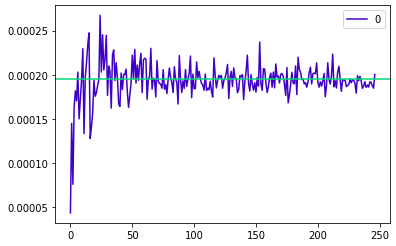
위의 그림에서 볼 수 있듯이 표본의 크기가 커질수록 모분산(민트색 선)에 가까워진다는 것을 확인할 수 있다.

중심극한정리 ( Central Limit Theorem, CLT )

Sample 데이터의 수가 많아질 수록, 샘플의 평균을 모아보면 모집단의 분포와 상관없이 정규분포를 따르게 된다.

샘플링을 할 때 가장 좋은 것은 모집단이 어떤 통계분포를 가지고 있는지 알고 있는 것이다. 모집단의 특성을 알고 있다면 표본이 모집단을 잘 대표할 수 있는지 판단하기도 쉽고 유의미한 인사이트를 도출하기 좀 더 수월하기 때문이다. 하지만 모집단의 특성을 정확하게 파악할 만큼의 돈과 시간이 부족하다는 이유 등으로 인해 보통은 분포를 모르는 경우가 많다.

표본평균의 히스토그램

sample_means = []

for x in range(0, len(population)):
   sample = np.random.choice(population, 100)
   sample_means.append(sample.mean())
  
# 표본평균 데이터에 대한 분포확인
pd.DataFrame(sample_means).hist(color = '#4000c7');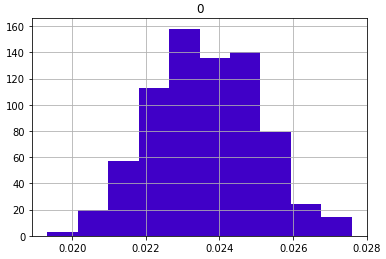

위의 그림은 표본평균들의 빈도수에 대한 히스토그램인데 종모양의 정규분포 모양을 가지고 있는 것을 알 수 있다. 위의 경우는 정규분포를 따르는 모집단이라면 다음은 푸아송분포를 따르는 모집단에서 사이즈가 20인 샘플을 뽑아서 보는 것이다.

sample_means2 = []

for x in range(0,1000):
  one_poiss = np.random.poisson(5, 20) # Poisson 분포 데이터, 람다가 5이고 20개 뽑는다.
  sample_means2.append(one_poiss.mean()) #평균

pd.DataFrame(sample_means2).hist(color = '#4000c7');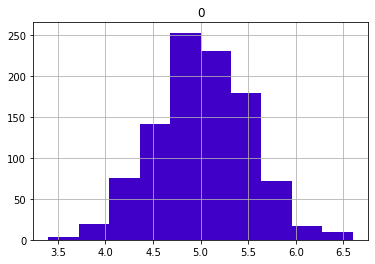

하지만 푸아송 분포를 따르는 모분산이라도 표본의 평균의 분포는 정규분포를 따른다는 것을 알 수 있다.

sampling의 중요성

샘플링을 여러 번 할수록 정확성이 높아지기도 하지만 샘플링을 어떻게 하느냐에 따라 정확성이 높아지기도 한다.

# 샘플을 10, 100, 700 으로 표본을 뽑아 표본에 대한 평균값 리스트에 쌓기
sample_means_small = []
sample_means_medium = []
sample_means_large = []

for x in range(0, 3000):
 #샘플을 10,100,700개로 뽑기
 small = np.random.choice(population, 10)
 medium = np.random.choice(population, 100)
 large = np.random.choice(population, 700)
 #각 샘플의 평균값을 모으기
 sample_means_small.append(small.mean())
 sample_means_medium.append(medium.mean())
 sample_means_large.append(large.mean())
 #
 ax = plt.subplots()

ax = plt.subplots()
# 표본을 적게 뽑은 평균 데이터의 히스토그램(빨강)
sns.histplot(sample_means_small, color = 'red')
# 표본을 중간 정도 뽑은 평균 데이터의 히스토그램(노랑)
sns.histplot(sample_means_medium, color = 'yellow')
# 표본을 많이 뽑은 평균 데이터의 히스토그램(초록)
sns.histplot(sample_means_large, color = 'green');
# 모집단의 평균 표현하기
plt.axvline(x=population.mean(), color='white', linestyle='--', linewidth=2)
plt.show()

# sample_means_small -> red 
# sample_means_medium -> yellow
# sample_means_large -> green
# population mean -> white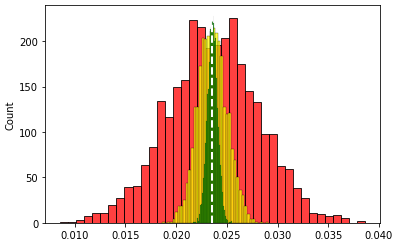

위의 그림처럼 모분산의 평균인 하얀 선에 표본이 많을수록 더 가까워지는 것을 볼 수 있으며 각각의 샘플들이 모두 정규분포를 따르고 있다는 점에서 큰 수의 법칙과 CLT를 모두 확인할 수 있다.

각주: ax에 대하여.

ax = plt.subplot()이해하기 참고문헌 1
ax = plt.subplot()이해하기 참고문헌 2

ax : A single object of the axes. Axes object if there is only one plot, or an array of axes. Axes objects if there are multiple plots, as specified by the nrows and ncols .

matplotlib 구성