💙 확률과 확률분포
- 확률
- 확률분포와 확률변수
- 주요 확률분포
확률 (probability)
💙 정의 💙
정한 조건 아래에서 어떤 사건이나 사상이 일어날 가능성의 정도
예) 동전 던지기에서 앞면이 나올 가능성, 주식 투자로 이익을 볼 가능성
기본 용어
- 표본점(sample point)
- 한 번의 실험 또는 관측으로부터 얻을 수 있는 결과
- 표본공간(sample space)
- 어떤 실험이나 관측에서 발생가능한 모든 결과의 집합
- 또는 로 표기
- 사상(event)
- 하나 또는 둘 이상의 단일 사상의 집합: 사건
- 표본공간의 부분 집합
확률의 종류
객관적 확률
실험이나 관찰의 필요에 따라 구분
 이미지출처
이미지출처
-
논리적 확률(수학적 확률, 고전적 확률)
- 어떤 한 시행에서 나타날 수 있는 결과의 개수(n)가 정해져 있음
- 각각의 결과가 나타날 가능성이 모두 동일할 것이라는 논리적 추론에 근거를 둠.
- 한계점
- 현실세계에서 단일사상이 발생할 가능성이 동일하지 않는 경우도 존재
(예) 특정한 치료법에 의해 질병이 치료될 확률 - 무한한 근원사상으로 이루어진 표본공간 존재
(예) 한 공정에서 불량품이 생산될 확률을 구하는 경우
- 현실세계에서 단일사상이 발생할 가능성이 동일하지 않는 경우도 존재
-
경험적 확률(통계적 확률)
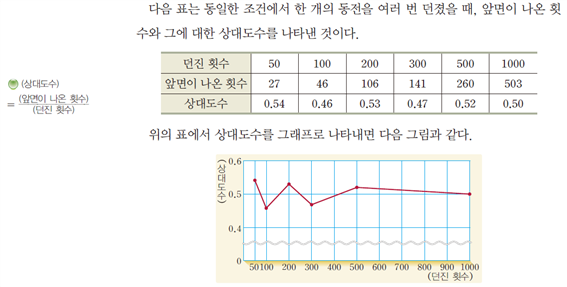
- 동일한 조건 하에서 같은 실험을 반복했을 때 어떤 특정한 사건(event)이 발생한 비율, 즉 상대도수로 계산.
- 실험의 반복 횟수는 충분히 커야 함.
 이미지출처
이미지출처
주관적 확률
- 논리적 확률, 경험적 확률 : 계산된 확률을 근간으로 하여 의사결정이 가능
- 특정사건이 발생할 가능성은 개인적인 지식과 경험 또는 가치관에 따라 달라질 수 있는 확률
(예) 야구에서 주자가 2루에 있을 때 감독은 어떤 대타를 기용할 것인인가?
공리적 해석
💡 참고
공리(公理, axiom) : 증명할 수는 없으나 옳다고 판단되는 명제
- A.N. Kolmogorov의 확률의 공리(확률론의 기초)
- 표본공간을 정의역으로 하며, 다음 세 가지 공리를 만족하는 함수를 확률로 정의
표본공간상에서 아래의 공리를 만족하는 P()를 확률측도(probability measure)라고 하고 P(A)를 사건 A의 확률이라고 합니다.
임의의 사상 A에 대하여
- 1) 0 1 : 어느 사건도 확률이 음수가 될 수 없고 1보다 클 수도 없음.
- 2) : 어떤 실험의 결과는 표본공간 S에서 항상 일어남
- 3) 서로 배반인 사상 에 대하여 를 만족할 때 P(A)를 사상 A의 확률이라고 한다.
위의 확률의 공리를 통해 알 수 있는 확률의 성질
확률의 기본 성질
주변확률, 결합확률, 조건부 확률

공리적 확률을 확장하면 주변확률, 결합확률, 조건부확률을 얻어낼 수 있다.
- 주변확률(marginal probability, 한계확률)
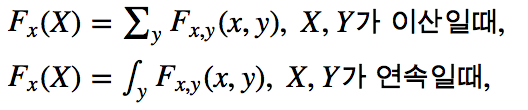
두 변수 중 한 변수만을 고려한 확률.
개별 사건의확률이지만 결합사건들의 합으로 표시될 수 있는 확률이다.
변수의 결합분포를 기록한 테이블에서 주변에 위치한 확률을 의미한다. X를 0으로 고정할 때 예를 들어보면 P(X=0,Y=0) + P(X=0,Y=1) = P(X=0)이 도출된다. X가 고정되었지만 Y값은 계속 변하는데 위의 확률은 Y값에 상관없이 X=0인 주변확률(한계확률)이라고 표현할 수 있다.
- 결합확률 (joint probability)
두 변수를 동시에 고려한 확률.
두 개의 사건이 동시에 일어날 확률로 서로 배반되는 두 사건 A, B가 있을 때 A와 B가 동시에 일어나는 확률())을 A와 B의 결합확률이라고 정의한다.
를 만족한다.
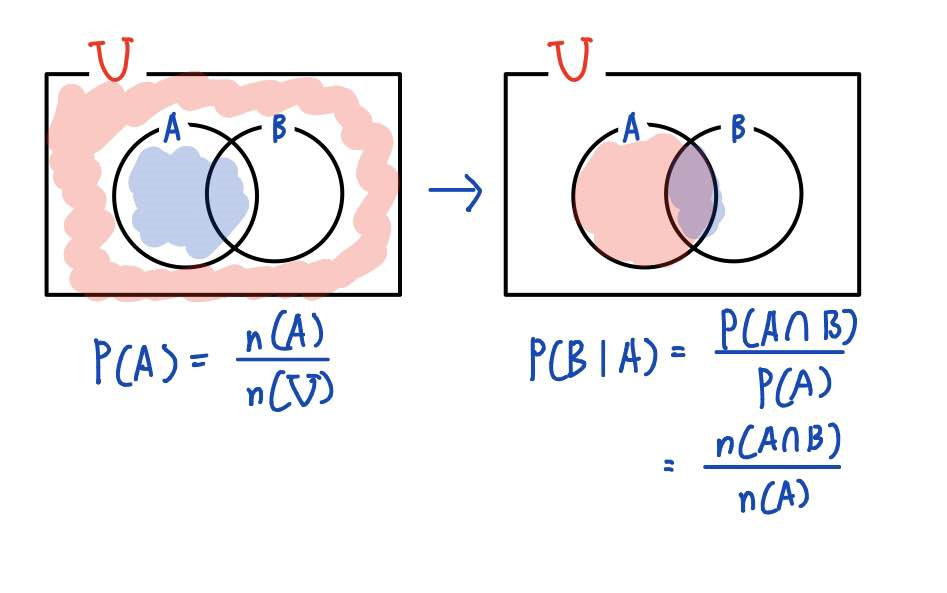
- 조건부확률(conditional probability)
조건부 확률이란 특정한 조건 하에서 어떤 사건이 발생할 확률이다.
즉, 어떤 사건 A가 일어났다는 전제 하에 사건 B가 발생할 확률이다.
조건부확률은 어떠한 사건 A가 일어났다는 전제를 가지고 확률을 정의하므로 표본공간은 A의 근원사건 k개로 이루어진표본 공간으로 재정의된다.
즉, 어떤 사건 A가 일어났다는 전제 하에 사건 B가 발생할 확률이 조건부확률이며 분자는 A와 B의 결합확률이 된다.
 이미지출처
이미지출처
- 주변확률, 결합확률, 조건부확률의 수리적 관계 (추가해야함)
확률분포와 확률변수
- 확률변수
- 실험이나 관찰의 결과값을 1:1 실수로 대응시키는 함수
- 일정한 확률로 나타나는(발생하는) 사건에 대해 숫자를 부여한 변수
- 확률분포
- 확률변수가 취할 수 있는 모든 값에 대해 각각의 확률을 대응시킨 것
