⭐️ 편향/분산의 트레이드오프 개념을 이해하고 일반화 관점에서 설명할 수 있다.
bias와 variance는 모델의 loss 또는 error를 의미한다.
🍒 편향(Bias)
편향은 학습 알고리즘에서 잘못된 가정으로 인한 오류이다. 편향이 높으면 알고리즘이 feature(설명변수, 독립변수)와 target(종속변수)간의 관계를 놓칠 수 있다. 특성과 타겟변수의 관계를 잘 파악하지 못하기 때문에 과소적합되는 것이다.
🍒 분산(Variance)
분산은 훈련 데이터셋의 작은 변동에 민감성으로 발생하는 오차이다. 분산이 높으면 모델이 학습 데이터의 노이즈에 민감하게 적합하여 테스트데이터에서 일반화를 잘못하는 경우로 과적합상태이다. 의도한 학습결과를 내기보다는 훈련 데이터 내의 무작위 소음을 모델링함에 따라 overfitting하게 될 수 있는 것이다.
bias vs variance
편향은 예측값들과 정답(실제값)이 대체로 멀리 떨어져 있으면 결과의 편향(bias)이 높다라고 한다. 예측값들이 자기들끼리 대체로 멀리 흩어져 있으면 결과의 분산(variance)가 높다라고 한다.
편향이 높다는것은 또한 train데이터의 오차가 크다는 것이다. 이는 과소적합으로 연결될 수 있으며 분산이 높다는 것은 train데이터에만 학습이되어 test데이터에서는 맞지않아 과적합으로 연결된다.
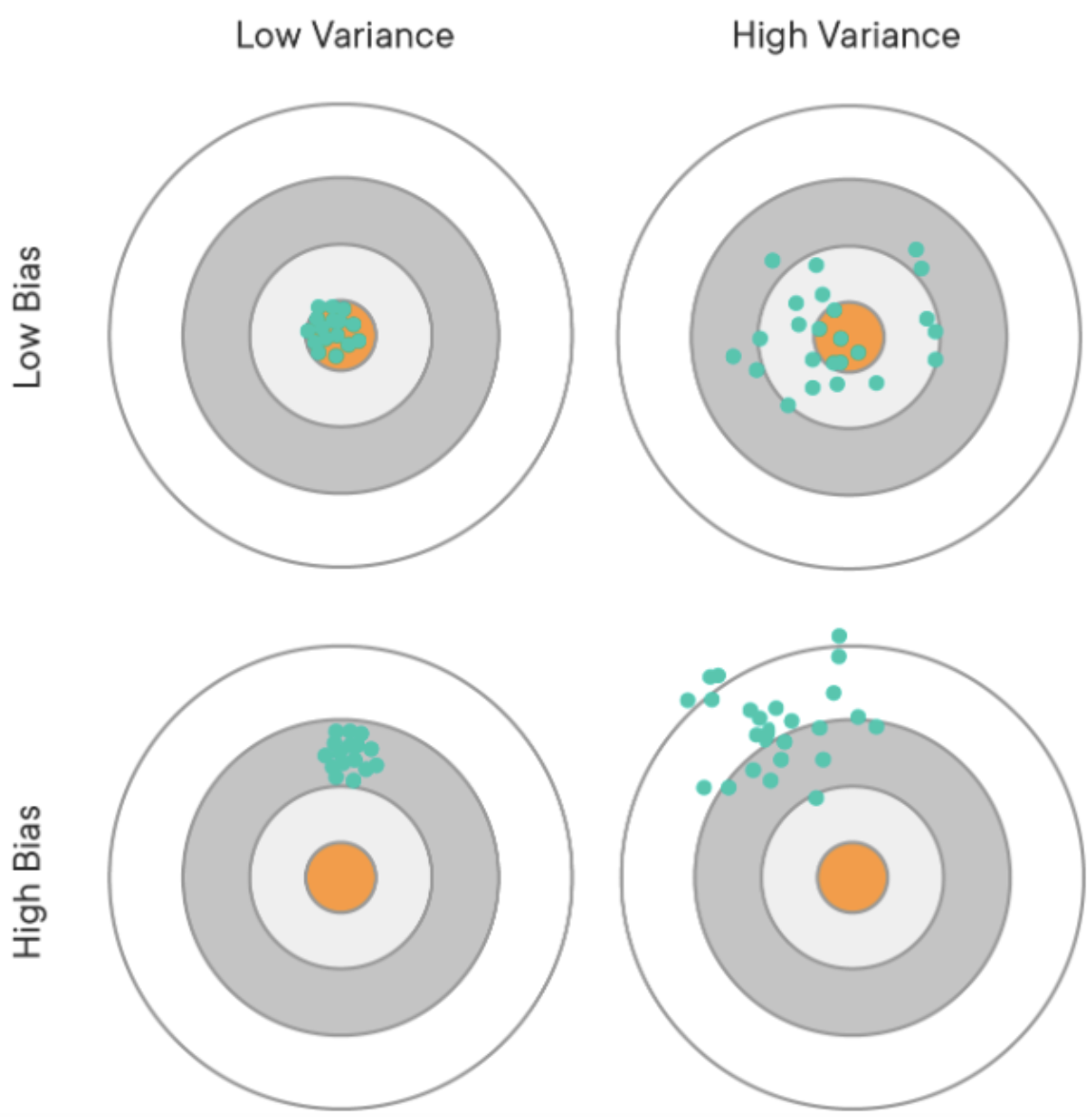
편향은 목표값(target)과 평균이 얼마나 떨어져 있는지를 나타내는 것이며, 분산은 표준편차의 제곱이다. 우리가 모델을 만들때는 편향과 분산을 최소로 만들어주어 에러를 줄이는것이 이상적이다.
🍒 편향-분산 트레이드오프
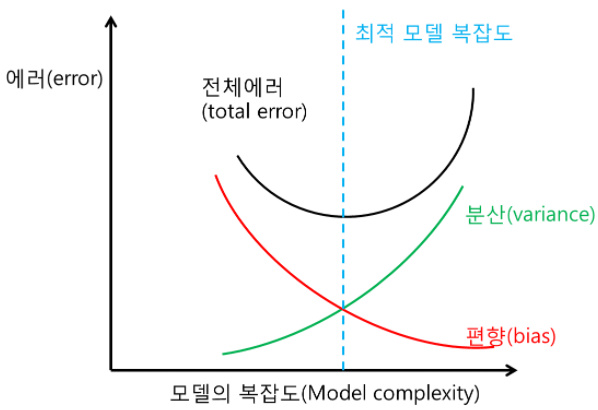
위의 그림은 모델복잡도와 에러를 편향과 분산의 관점에서 바라본 그래프이다.
분산이 낮을수록 편향이 높아지며(Underfitting), 분산이 높을수록 편향이 낮아지는(Overfitting)것을 볼 수 있다.
에러를 가장 낮게하는(편향과 분산이 낮은지점에서 교차가되는)곳까지만 학습을 시켜야 한다.
요약하면 우리는 편향과 분산을 완벽하게 제거하지 못한다. 하지만 편향이나 분산 중 하나을 완벽히 제거하고자 한다면 다른 하나가 커져 좋은 모델에서 멀어지게 된다. 따라서 우리는 편향과 분산사이에서 균형 즉,편향과 분산의 트레이드 오프를 찾아야한다.
