트리 Tree
트리란? Tree
그래프의 일종으로, 여러 개의 노드(Node)와 노드를 연결하는 간선(Edge)으로 구성된 자료구조다.
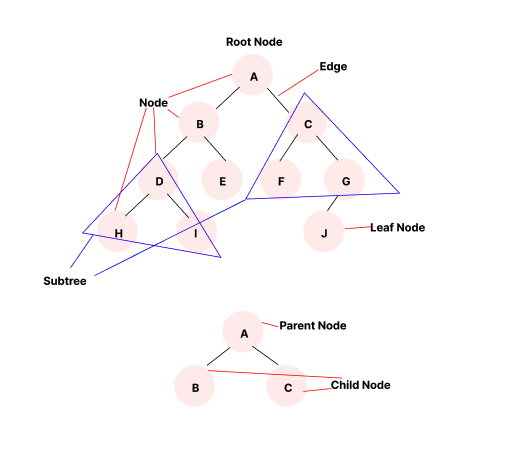
노드란? Node
트리는 하나 이상의 노드로 구성된다
각 노드는 데이터를 저장할 수 있으며, 연결된 간선으로 다른 노드와의 관계를 가진다.
간선이란? Edge
트리의 간선은 노드와 노드를 연결하는 선을 의미한다.
방향이 없는 경우와 방향이 있는 경우가 있는데,
방향이 없는 간선을 무방향 간선 Undirected Edge
방향이 있는 간선을 유향 간선 Directed Edge
루트 노드란? Root Node
트리는 하나의 루트 노드를 가진다.
루트 노드는 다른 모든 노드들의 조상이라고 생각하면 편하다.
부모 노드가 없는 유일한 노드이다.
부모노드와 자식 노드란? Parent Node Child Node
각 노드는 최대 하나의 부모 노드와 여러 개의 자식 노드를 가질 수 있다.
부모 노드와 연결된 간선(Edge)을 부모-자식 간선(Parent-Child Edge)라고 한다.
리프노드란? Leaf Node
자식 노드가 없는 노드를 리프노드 또는 단말 노드(Terminal Node)라고 한다.
즉, 리프 노드는 더 이상 자식 노드를 갖지 않는 마지막 노드이다.
서브 트리란? Subtree
각 노드는 자신을 루트로 하는 서브트리를 가질 수 있다.
서브트리는 해당 노드와 그 자손 노드들의 집합니다.
트리는 계층 구조를 가지며, 일반적으로 상위 노드에서 하위 노드로 내려가면서 계층적인 구조를 표현한다.
이러한 구조로 인해 트리는 데이터 구조, 그래프 알고리즘, 운영체제 등에서 다양하게 활용된다.
트리 깊이란? depth
루트에서 해당 노드까지의 경로 길이를 의미한다.
즉, 루트에서 해당 노드까지 내려오는 간선(Edge)의 개수를 의미한다.
깊이가 0인 노드는 루트 노드이다.
(+ 추가설명 필요)
트리 높이란? height
루트에서 해당 노드까지의 최장 경로 길이를 의미한다.
트리에서 가장 깊은 노드의 깊이를 의미한다.
즉, 트리에서 가장 멀리 떨어져있는 리프(leaf) 노드까지의 경로 길이를 의미한다.
트리의 높이는 트리에서 가장 깊숙히 있는 노드의 깊이를 의미한다
(+ 추가 설명 필요)
이진트리란? Binary Tree
각각의 노드가 최대 2개의 자식노드를 가지는 트리 자료구조를 의미한다.
이진트리는 데이터 검색 및 정렬에 자주 사용된다.
각각의 노드는 자식 노드가 없을 수도 있고, 하나의 자식 노드만 가질 수도 있다.
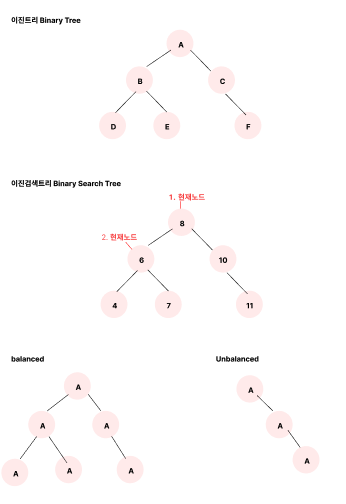
이진검색트리란? Binary Search Tree
현재 노드 안의 데이터가 왼쪽노드와 그 이하 자식노드들은 현재 노드보다 작아야하고, 오른쪽 노드와 그 이하 자식노드들은 현재노드보다 커야한다.
balance
balance가 맞다 안맞다는 왼쪽 오른쪽 개수가 정확하게 일치해야한다는 말이 아니다.
너무 지나치게 치우쳐져 있지만 않으면 balance가 맞다고 표현된다.
balance가 맞는 대표적인 트리로는 red-black tree, AVL tree가 있다.
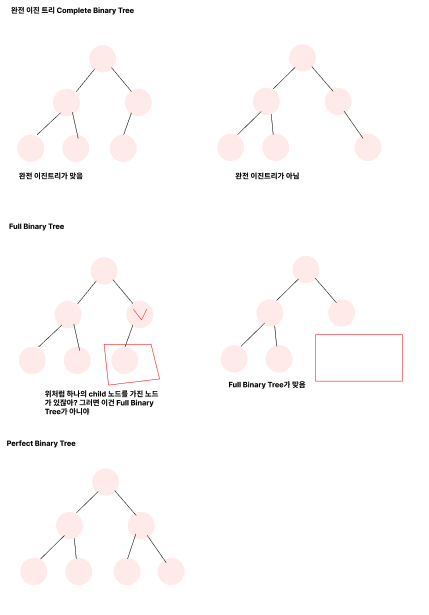
완전이진트리 Complete Binary Tree
모든 노드들이 레벨별로 왼쪽부터 채워져 있으면 완전이진트리이다
트리를 만들다보면 레벨이 생기는데 그 마지막 레벨을 제외한 모든 서브트리의 레벨트리가 같아야하고, 마지막 레벨은 왼쪽부터 채워져있으면 완전이진트리이다.
Full Binary Tree
하나의 Child노드를 가진 노드가 하나도 없는게 Full Binary Tree라고 한다.
Full Binary Tree가 되려면 그 안의 노드들이 Child를 안가져야한다. Child를 안가지려면 하나도 갖지말고, 가지려면 2개를 가져야한다.
(유어클래스에서는 '정 이진 트리'라고 한다)
Perfect Binary Tree
양쪽으로 빈공간없이 모든 노드가 두 개의 자식을 가지고 레벨도 정확하게 딱 떨어져야 한다. 완벽하게 피라미드 구조를 가진 형태이다.
(유어클래스에서는 '포화이진트리'라고 한다)
=> 2^n - 1 개의 노드를 가지는게 바로 Perfect Binary Tree이다.
