시간 복잡도 키워드 : 빅오표기법/시간과 함수의 관계/상수시간/선형시간/평방시간/로그시간
시간 복잡도란 ?
- (위키에서) 문제를 해결하는데 걸리는 시간과 입력의 함수관계.
- 입력값에 변화에 따라 연산을 실행할 때, 연산 횟수에 비해 걸리는 시간을 나타낸 것
- 계산법 : 핵심이 되는 연산이 무엇일까
빅오표기법 (BigO)
- 빅오표기법은 시간복잡도를 표현하는 방법입니다.
- 각각 최악, 최선, 중간(평균)의 경우에 대하여 나타내는 방법
- 일반적으로 시간복잡도를 표현할때 빅오표기법으로 나타낸다.
Big-O(빅-오)
Big-Ω(빅-오메가)
Big-θ(빅-세타)
O(1) 상수시간
- 입력 크기(개수)에 관계 없이 수행 속도(계산 횟수) 일정 (ex/ 배열에 있는 항목을 인덱스를 사용하여 접근할때)
O(1)는 입력값이 아무리 증가해도 시간이 늘어나지 않는 경우입니다.
배열의 길이가 아무리 길어도 해당하는 인덱스에 접근하는 시간은 동일합니다.
인풋이 얼마나 크든 말든, 관계 없이 함수는 동일한 수의 스탭이 필요하다.
이 함수의 시간 복잡도는 constant time(상수 시간)이라고 할 수 있다.
N이 얼마나 크든 관계 없이 끝내는데 동일한 숫자의 스탭이 필요하다.
함수의 인풋 사이즈가 엄청나게 커져도 관계 없이 미리 정해진 숫자에 따라 작동한다.
function 0_1 (arr, index) {
return arr[index];
}
let arr = [1,2,3,4];
let index = 1;
console.log(0_1(arr, index)) // 2예를 들면, 항상 200개의 스탭이 필요한 함수가 있다면, 인풋 사이즈와 관계 없이 함수의 시간의 복잡도는 O(200)이 아니라 여전히 O(1)이다.여전이 constant time (일정한 시간/상수)이다. 인풋 사이즈와 관계 없이 스탭이 정해진 알고리즘이다.

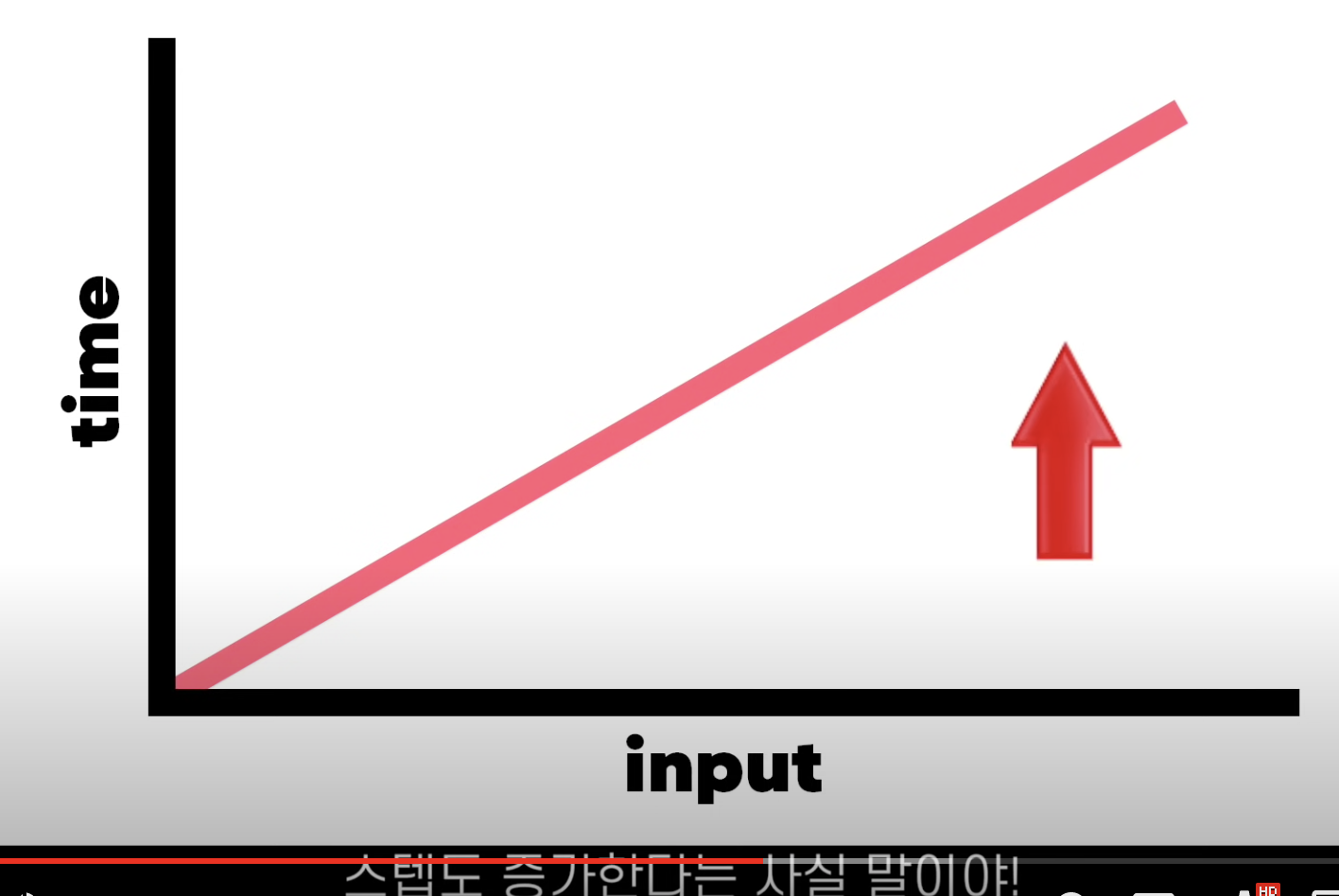
O(n) 선형시간
- 입력 개수에 단순 비례적으로 수행시간이 길어짐. (ex/ 반복문, 선형 검색, 자연수의 거듭제곱)
인풋이 증가하면 스탭도 증가한다. 입력값이 1일때 1초의 시간이 걸리면, 입력값이 100일때 100초의 시간이 걸린다. 최악의 경우, 입력 개수만큼 연산을 수행한다.
// O_N(n)에서 n의 시간이 걸리고, another_0_n(n)에서 2n의 시간이 걸린다. 총 3n이 걸리지만, 빅오표기법에서는 계수의 크기에 상관없이 O(n)으로 표현한다. 다른 알고리즘이 추가되어 3n+1같은 시간이 걸려도 상수를 무시하고 O(n)로 표현한다.
function 0_n(n) {
for (let i=0; i<n; i++) {// do sth}
}
function another_0_n(n) {
for (let i=0; i<2n; i++) {// do sth}
}
O(n²) 평방시간
- 문제 해결 단계의 수가 입력값 n의 제곱으로 증가 (ex/ nested loop, 버블정렬, 삽입정렬, 선택정렬)
Quadatic time 2차 시간이 있다. 2차 시간은 Nested Loops (중첩 반복)이 있을때 발생한다. 중첩 반복문은 배열의 각 아이템에 대하여 루프를 반복하여 실행한다. 3중 for문을 사용해도 O(n²)로 표현한다.
예를 들어 20개의 데이터는 400개의 스탭이 될 것이다.
function algorithm(n) {
for (let i = 0; i < n; i++) {
for (let j = 0; j < n; j++) {
for(let k = 0; k < n; k++){
// do something
}
}
}
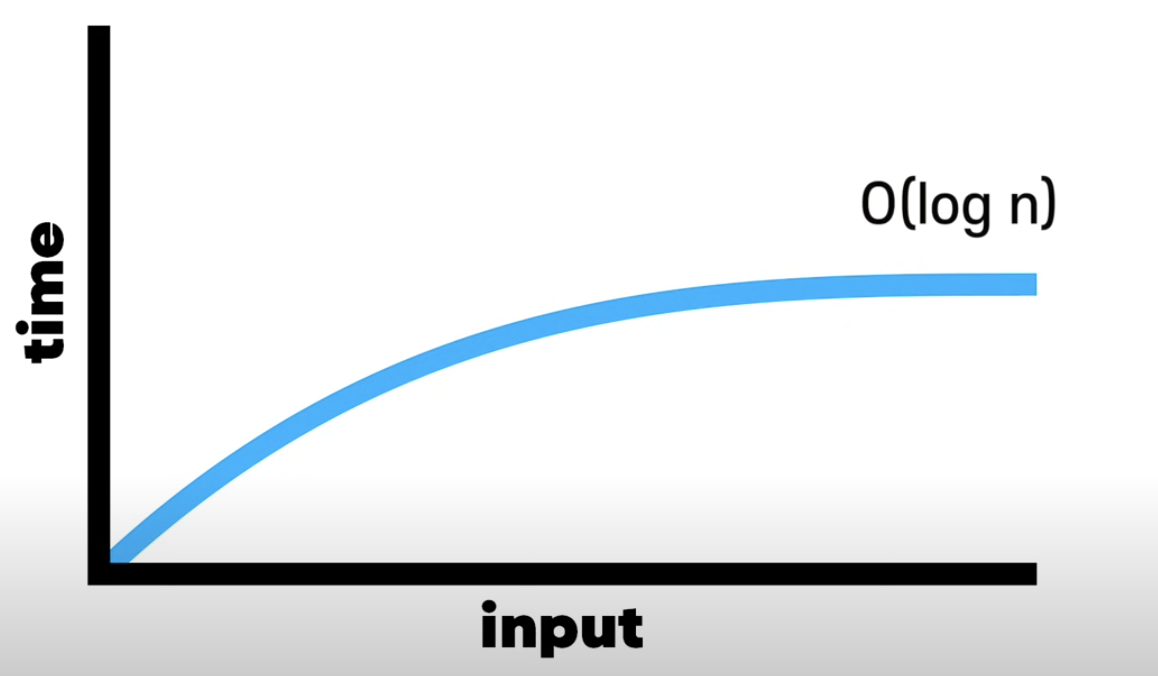
}O(log N) 로그시간
- 데이터가 2배로 증가할때, 연산수가 1단계씩 늘어나는 형태 (ex/ 이진 검색 BST)
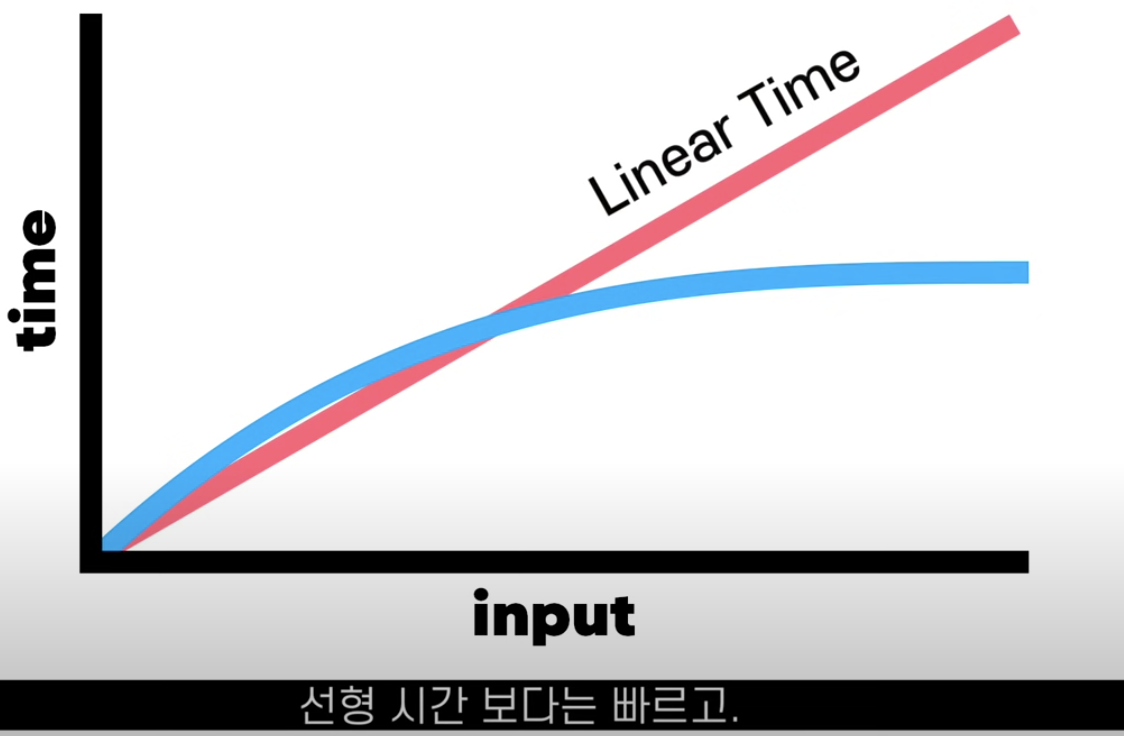
- lon n이기 때문에 O(n) 선형시간보다 빠르다.
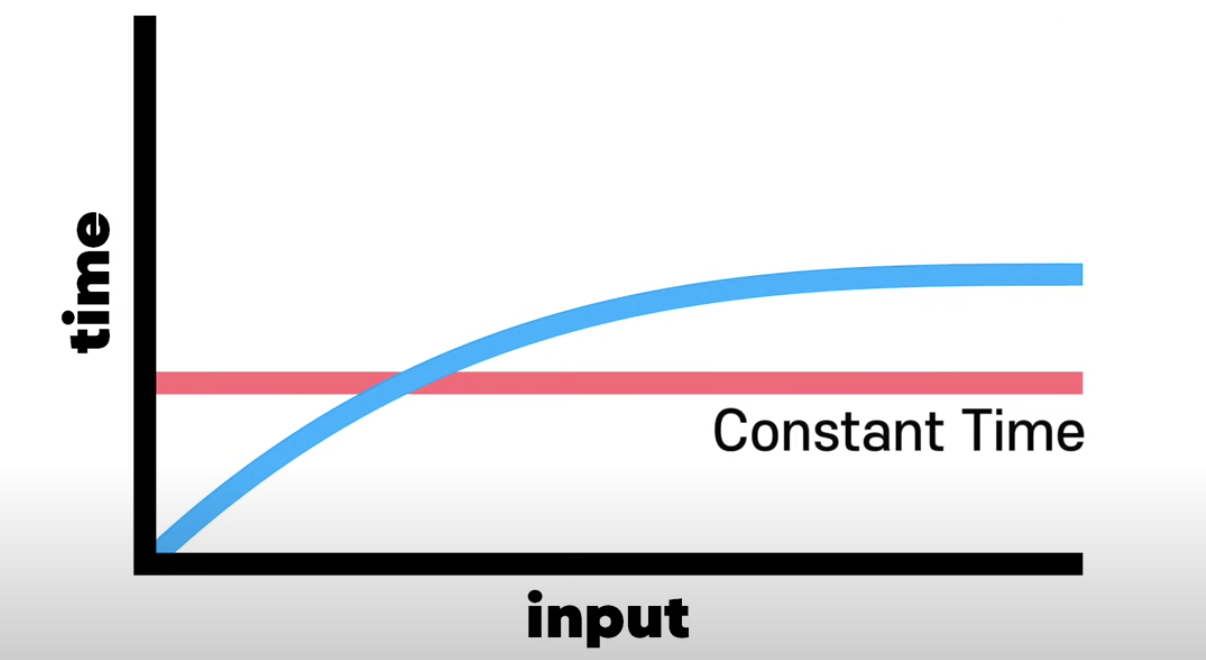
Logarithmic time 로그 시간이 있다. 로그는 지수(ex/2의 5 제곱은 32)의 정 반대다. 이진 검색의 시간 복잡도는 O(n) 선형 시간보다 빠르고 O(1) 상수 시간보다는 느리다.
로그의 예시
32의 밑이 2인 로그는 무엇일까. 32을 2로 몇 번을 나눠야 1일 나올까? 32/2=6 16/2=8
8/2=4 4/2=2 2/2=1. 32의 밑이 2인 로그는 5이다.
결론, 알고리즘의 시간복잡도를 인풋과 연관하여 빠르게 알아낼 수 있다.
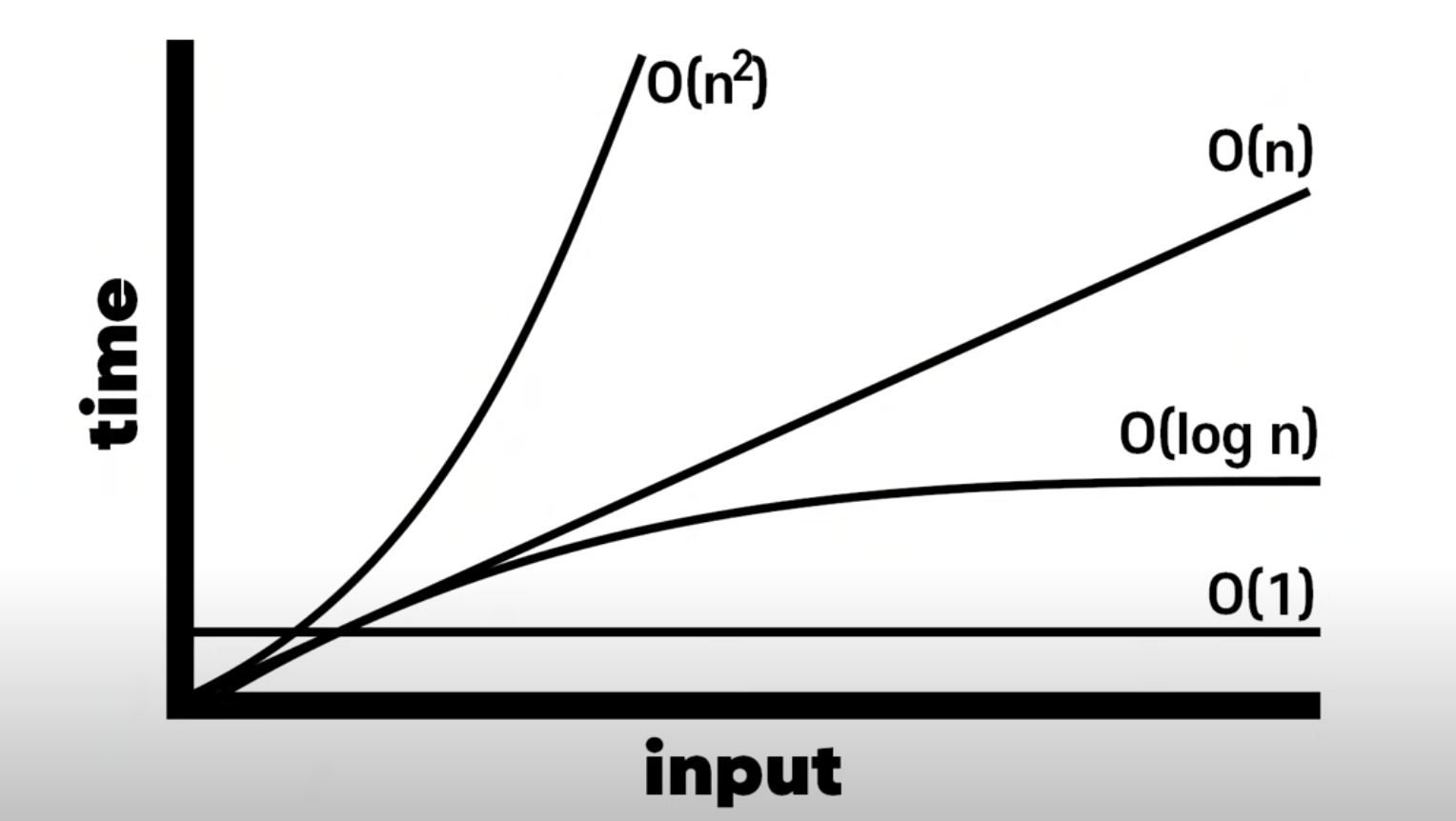
reference
https://velog.io/@ghwnd6448/%EC%8B%9C%EA%B0%84%EB%B3%B5%EC%9E%A1%EB%8F%84
https://www.youtube.com/watch?v=BEVnxbxBqi8
http://www.ktword.co.kr/test/view/view.php?m_temp1=6146
